Планиметрия на Всесибе
Ошибка.
Попробуйте повторить позже
Отрезок точками
и
разбит на три отрезка
и
из которых можно составить треугольник. Найти все точки
лежащие внутри отрезка
для произвольного такого разбиения.
Источники:
Подсказка 1
Посмотрите, что нам дано в задаче, например, как воспользоваться условием о том, что из отрезков можно составить треугольник?
Подсказка 2
Это означает, что отрезки удовлетворяют неравенству треугольника. Попробуйте понять, где будет лежать точка M на отрезке AB.
Подсказка 3
Из неравенства треугольника AP + PM > MB, но тогда AP + PM > AB/2, следовательно, точка M всегда лежит правее отрезка AB.
Подсказка 4
Проведите аналогичные рассуждения для точки P.
Подсказка 5
Выходит, что середина отрезка AB всегда лежит между точками P и M. А найдутся ли другие?
Подсказка 6
Возьмем точку X, отличную от центра (обозначим его за O). Пусть X лежит между O и A. Может стоит взять какую-нибудь "хорошую" точку за P?
Подсказка 7
Пусть P — середина OX, а M — точка, симметричная P относительно O.
Подсказка 8
Попробуйте через неравенство треугольника доказать, что точка X не лежит на отрезке PM.
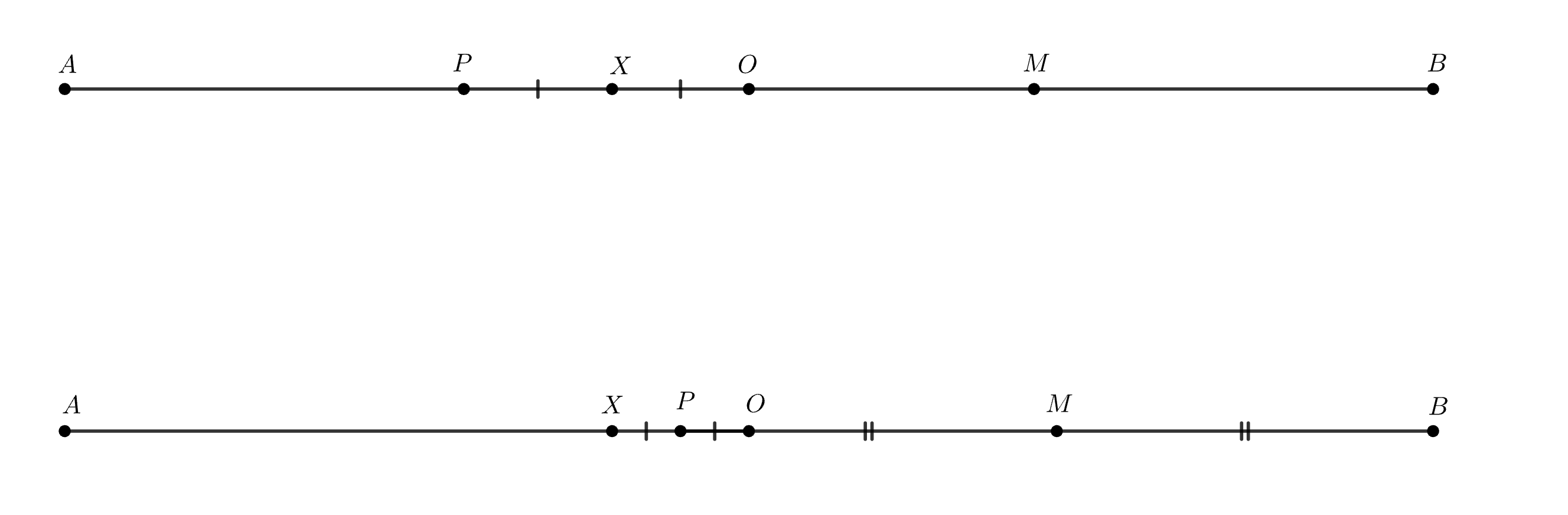
По неравенству треугольника
Поэтому
Следовательно, точка всегда лежит правее середины отрезка
Аналогично,
Поэтому
Следовательно, точка всегда лежит левее середины отрезка
Значит, середина
отрезка
всегда лежит
строго между точками
и
то есть лежит внутри отрезка
для любого разбиения
точками
и
из
условия.
Докажем, что больше таких точек нет. Рассмотрим произвольную внутреннюю точку отрезка
отличную от
Не умаляя
общности будем считать, что
лежит между
и
Обозначим за
середину отрезка
а за
— точку, симметричную
относительно
Тогда
Следовательно,
Значит, из отрезков
и
можно составить равнобедренный треугольник, и мы построили «треугольное» разбиение
в
котором точка
не лежит в отрезке
Другой способ выбора точек и
для
за
возьмём середину
за
— середину
Тогда
Следовательно, из отрезков
и
можно составить равнобедренный треугольник. Тогда мы построили «треугольное»
разбиение
в котором точка
не лежит на отрезке
Середина отрезка
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




