Стереометрия на ПВГ
Ошибка.
Попробуйте повторить позже
На основании прямого кругового конуса расположены три попарно касающихся друг друга шара одинакового радиуса. Каждый из них
касается также боковой поверхности конуса. Четвёртый шар того же радиуса касается первых трёх и боковой поверхности конуса. Найдите
объём конуса, если радиус окружности, образованной точками касания четвёртым шаром боковой поверхности конуса, равен
.
Источники:
Подсказка 1
Попробуйте представить расположение шаров. Какой фигурой можно описать их центры?
Подсказка 2
Правильно, центры шаров образуют правильный тетраэдр. Теперь нужно заметить, с чем ещё совпадает угол между высотой и боковым ребром тетраэдера?
Подсказка 3
Он совпадает с углом между высотой и образующей конуса и углом между радиусом окружности из условия и радиусом четвёртого шара, если они проведены в одну точку. Как можно найти этот угол?
Подсказка 4
Выразим sin и cos этого угла через стороны тетраэдра. Теперь нам нужно понять, из каких отрезков состоит образующая конуса.
Подсказка 5
Он состоит из расстояния от вершины конуса до точки касания четвёртого шара, расстояния между точками касания нижнего и верхнего шаров и расстояния от основания конуса до точки касания нижнего шара. Теперь, если сложим их, то найдем образующую. Останется только найти через неё объём конуса!
Центры шаров образуют правильный тетраэдр. Угол между высотой и боковым ребром рассчитается и совпадает с углом между высотой
и образующей конуса, а также с углом между радиусом упомянутой в условии окружности и радиусом 4-го шара, проведенными в одну
точку.
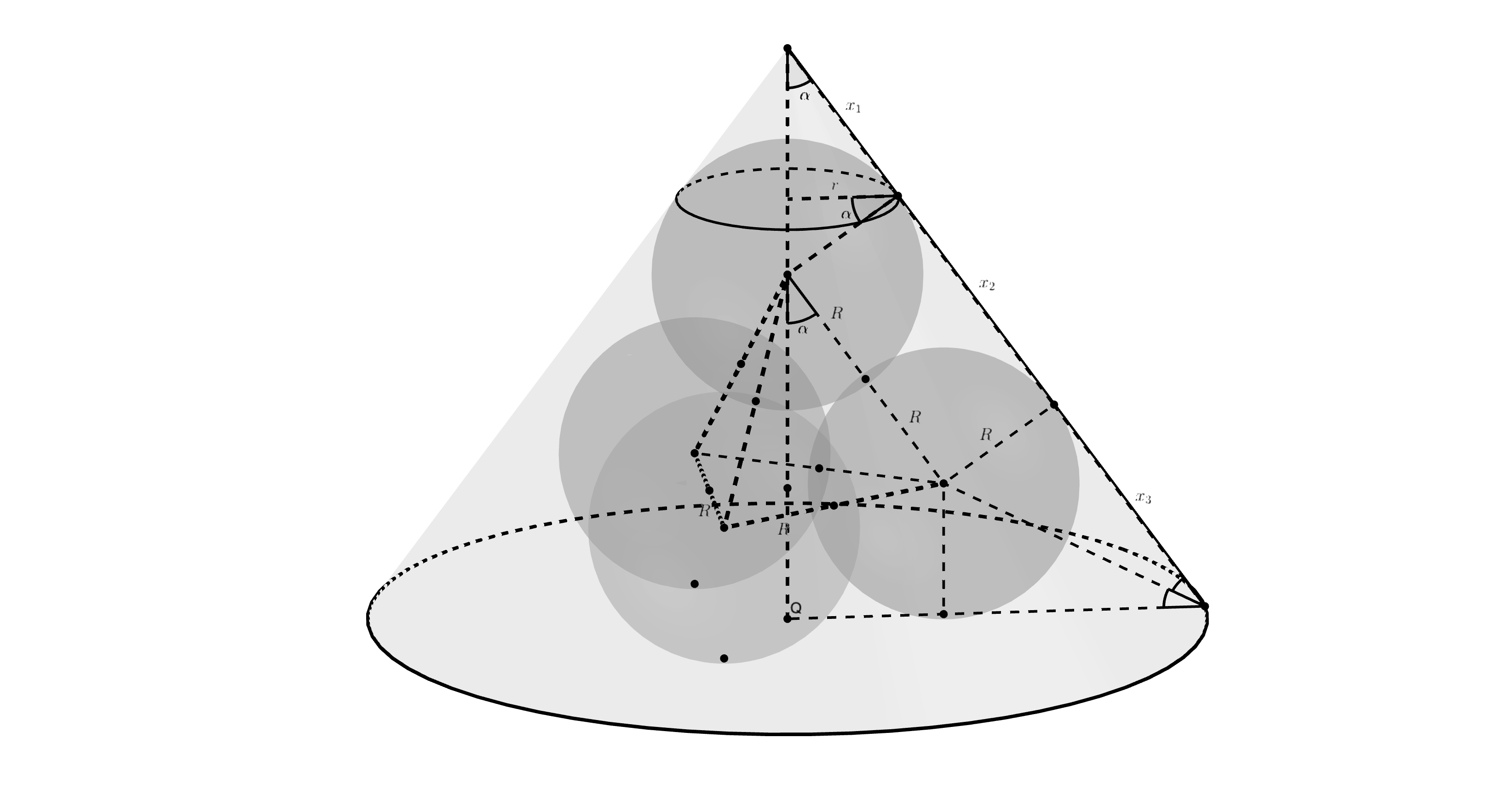
Пусть — указанный угол. Тогда
Пусть
— радиус окружности в плоскости касания конуса четвертым
шаром. Образующая
собирается из кусочков:
1) (от вершины конуса до точки касания конуса четвертым шаром);
2) где
— радиусы шаров (расстояние между двумя точками касания — нижнего и верхнего шаров соответственно);
3) ( расстояние от основания конуса до точки касания нижнего шара).
Заметим, что следовательно,
и
Итого
Объем конуса
После всех подстановок и упрощений получаем
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




