Стереометрия на ПВГ

Пусть — общая вершина рассматриваемых конусов, и — их оси. Обозначим через и их общие образующие и через искомый угол . Описанная в задаче конфигурация имеет две плоскости симметрии: одна — — содержит оси конусов, другая — — содержит их образующие. Тогда эти плоскости перпендикулярны. Пусть — прямая их пересечения.

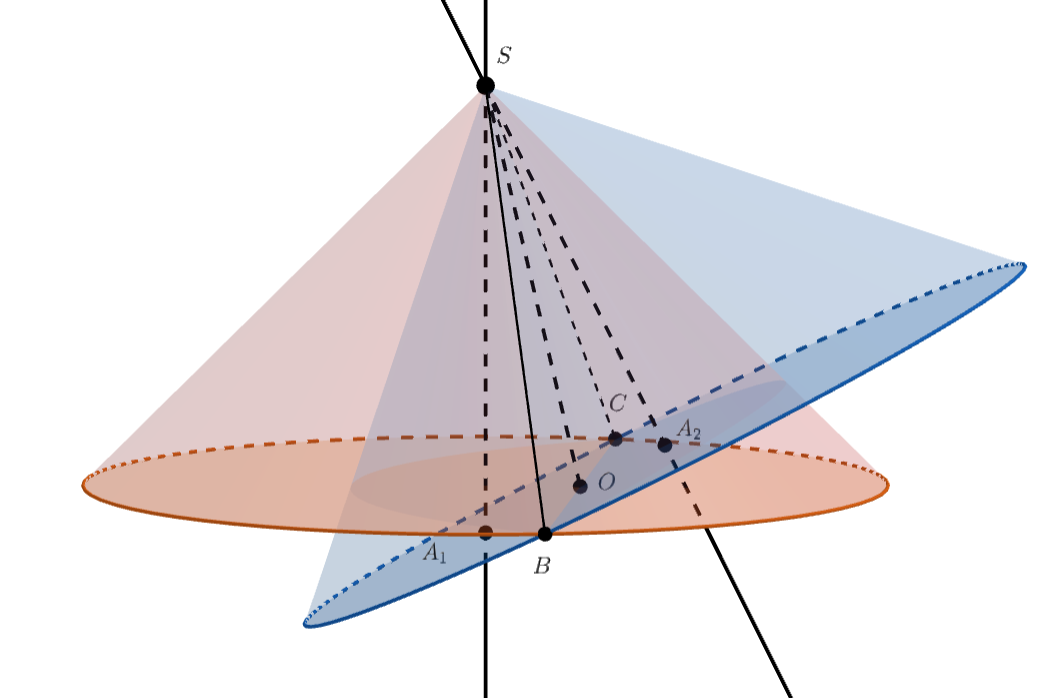
Обозначим через угол при вершине в осевом сечении каждого из конусов. Так как является образующей для конуса с осью и наоборот, то . Кроме того,

Точки можно выбирать произвольно на прямых Будем считать, что точки лежат в некоторой плоскости, перпендикулярной прямой и расположенной на расстояние от вершины . Тогда из пирамиды , в которой все плоские углы при вершине прямые, имеем

Тогда по теореме косинусов для треугольников и

Приравняем эти выражения, сократим на и применим основное тригонометрическое тождество в виде

Мы знаем, что , поэтому