Планиметрия на Ломоносове
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике площади треугольников
и
равны, а площадь треугольника
равна
половине площади треугольника
Найдите длину отрезка
где
— середина стороны
если известно, что
Подсказка 1
Попробуем раскручивать задачу постепенно и будем записывать равенства площадей из условия. Раз уж нужны площади, почему бы тогда не опустить высоты в них?)
Подсказка 2
Опустим высоты из A и C на BD. Что можно сказать об их длинах? Быть может, это влечет за собой другие равенства треугольников?
Подсказка 3
Высоты равны, поэтому появляются еще и равные треугольники! Пусть O — точка пересечения диагоналей нашего четырёхугольника. Что можно сказать о треугольнике ACD?
Подсказка 4
В треугольнике ACD проведена медиана DO! Тогда можно обозначить площадь треугольника ADO за x и записать уравнение на площади из условия)
Подсказка 5
Итак, теперь мы знаем, какую часть треугольника ABD составляет треугольник ADO. Что тогда полезного можно отметить на BO?
Подсказка 6
Отметьте на BO точку, делящую отрезок в отношении 2:1, считая от вершины ;)
Опустим высоты и
на
из точек
и
соответственно.
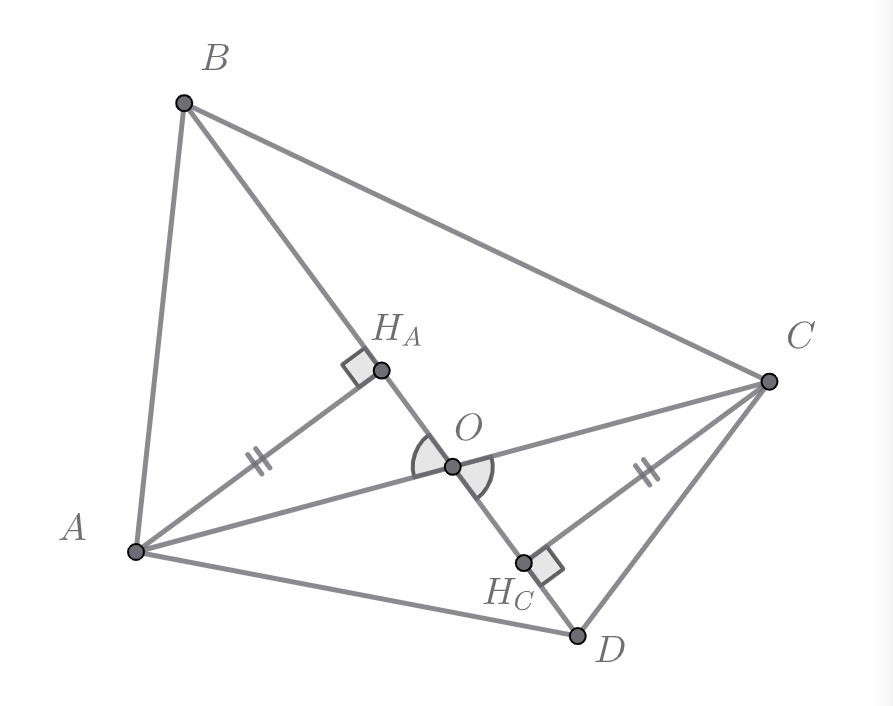
Воспользуемся равенством площадей и
Значит, высоты и
равны. Тогда из равенства прямоугольных треугольников
и
следует
равенство отрезков
и
А так как медиана делит треугольник на два равновеликих, то пусть
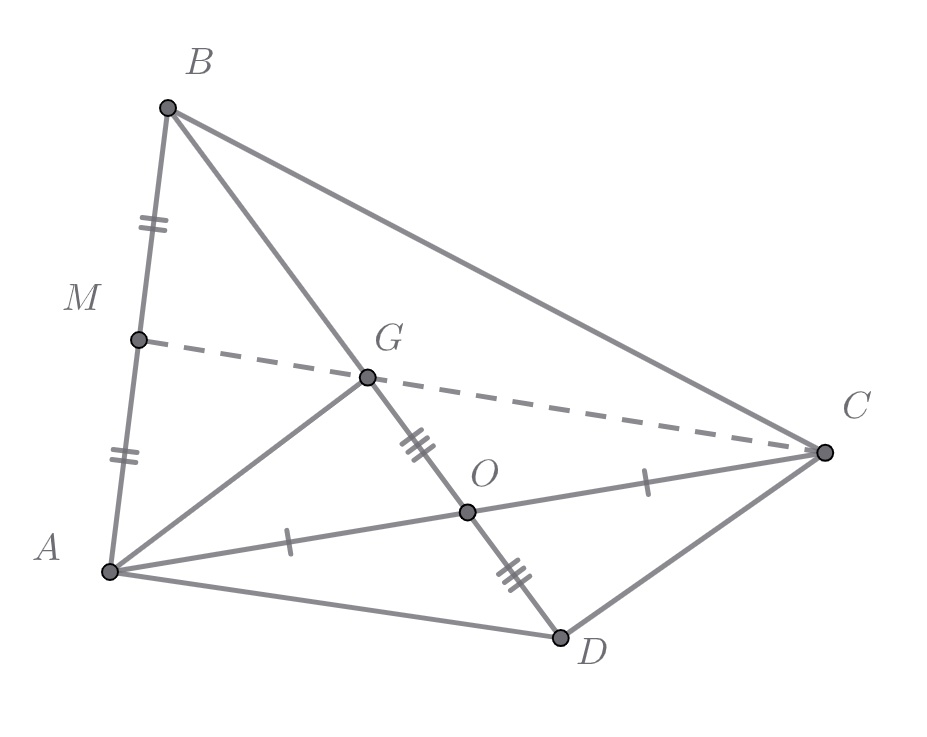
По условию дано, что Перепишем в виде:
Откуда получаем Если на
отметить точку
, такую что
то
Из равенства
следует, что
Так как выше уже получили равенство
то
— параллелограмм и
Вспомним, что на медиане была отмечена точка, делящая данный отрезок в том же отношении, что и точка пересечения медиан.
Значит, точка
и есть центр масс. Следовательно,
Собирая найденные факты воедино, получаем:
18
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




