Планиметрия на Ломоносове
Ошибка.
Попробуйте повторить позже
В окружность радиуса 3 вписан четырёхугольник, три стороны которого равны Найдите максимально возможную площадь
такого четырёхугольника.
Источники:
Подсказка 1
Сначала начертим сам четырёхугольник с окружностью, а потом соединим его вершины с центром окружности. Что мы можем сказать про получившиеся треугольники?
Подсказка 2
Нетрудно заметить, что два из них — равные правильные (со стороной 3), другой — прямоугольный с катетами 3 и гипотенузой 3√2. Их площади легко найти, так что разберёмся с оставшимся. Как можем найти его площадь (знаем как минимум две его стороны)?
Подсказка 3
Вспомним, что можно вычислить площадь прямоугольника через полупроизведение двух его сторон и синусу угла между ними. Так как все про остальные треугольники мы знаем, то и градусную меру этого центрального угла легко можем найти. Считаем оставшуюся площадь и складываем с площадями всех остальных треугольников, получая ответ.
Первое решение.
Решим задачу в общем случае. Обозначим четырехугольник Пусть
В такой конфигурации угол
между сторонами
и
равен
Угол
как противолежащий.
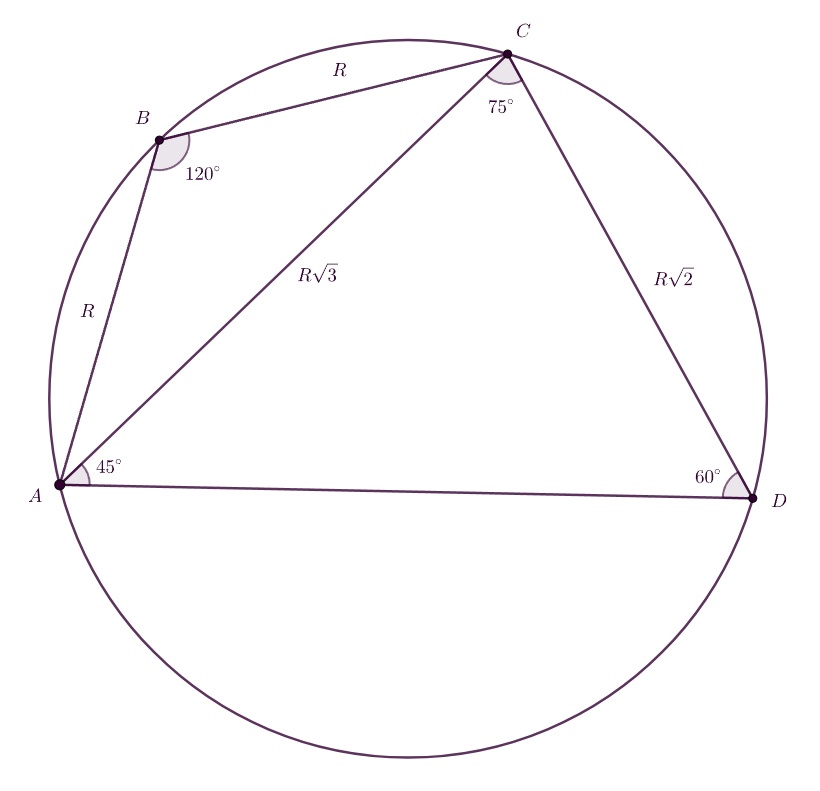
Диагональ Из теоремы синусов для треугольника
следует, что угол
равен
(угол
острый, т.к.
иначе
и сумма углов треугольника
будет больше
). Значит, угол
равен
Площадь
четырехугольника можно вычислить, как сумму площадей треугольников
и
Возможна другая конфигурация:
В этом случае четырехугольник — равнобочная трапеция с углом при
основании
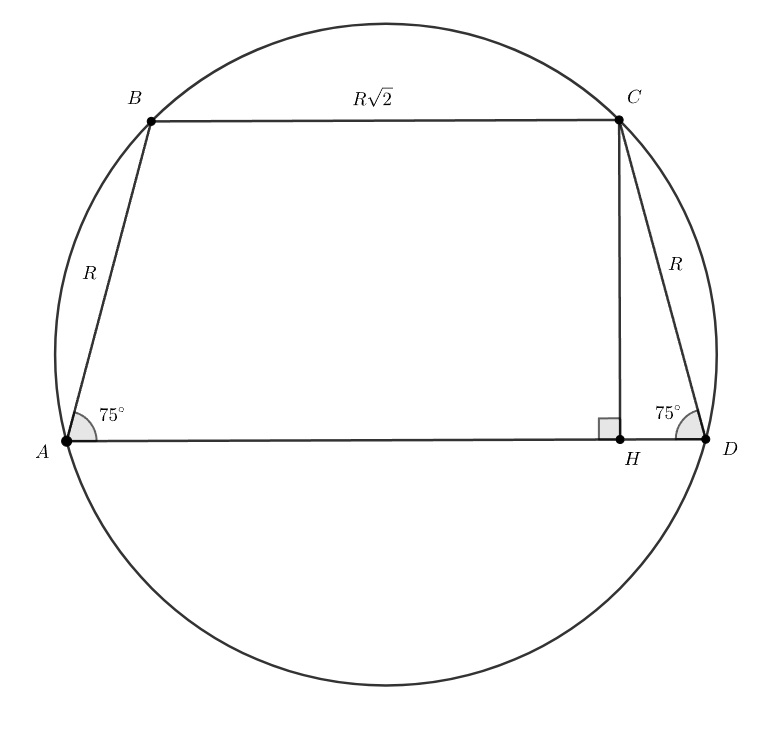
Тогда высота и площадь трапеции равна
Оба варианта одинаковые, при подставновки ответ равен
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
Соединим вершины четырехугольника с центром окружности.
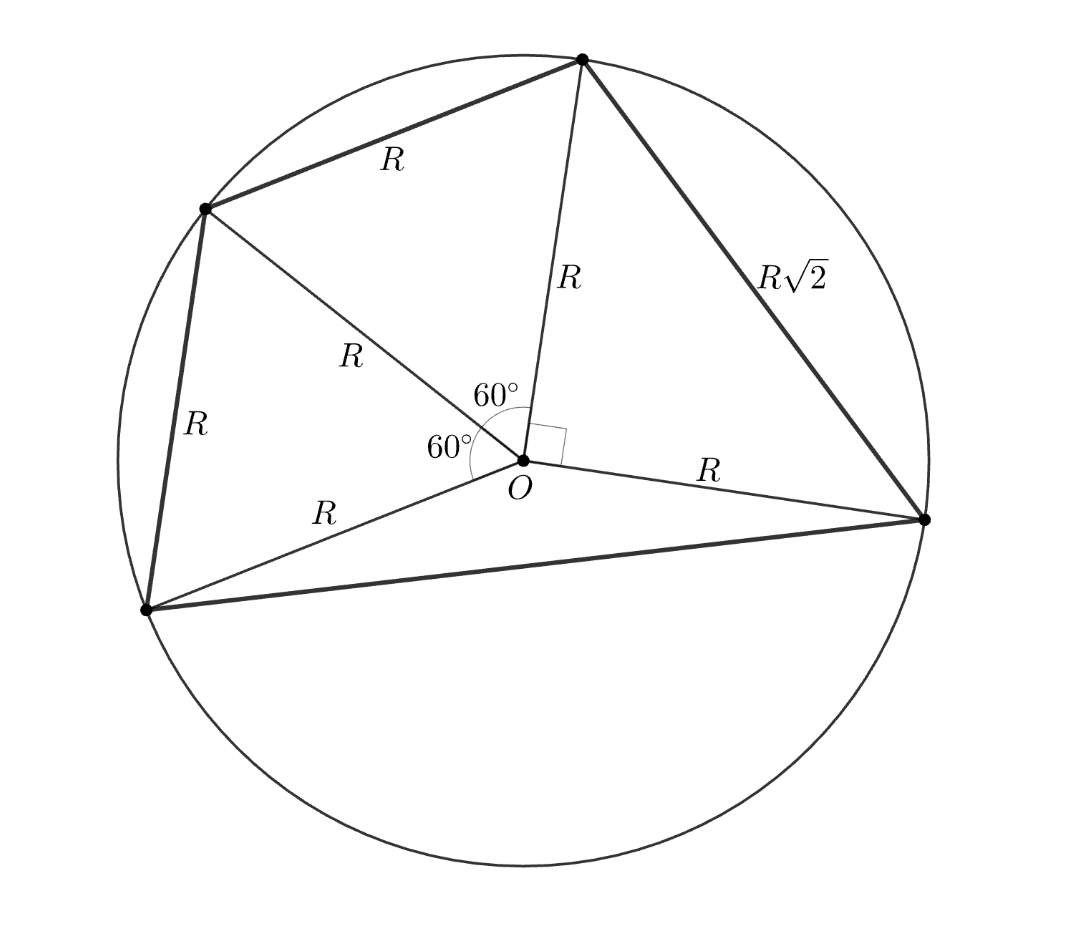
Получается, что четырехугольник составлен из двух правильных треугольников со стороной 3, площадь каждого одного
прямоугольного треугольника с катетами 3, 3 и гипотенузой
площадь
одного равнобедренного треугольника со сторонами 3 и 3 и
углом между ними
площадь равна
Суммарная площадь одинакова вне зависимости от того, в каком порядке они расположены, и равна
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




