Планиметрия на Ломоносове
Ошибка.
Попробуйте повторить позже
Газонная поливалка равномерно разбрызгивает вокруг себя воду в круге радиуса 
На границе этого круга расположена другая
такая же поливалка. А ровно посередине между двумя поливалками находится вход в нору. Мышь, хозяйка норы, хочет вернуться домой, но
не хочет сильно вымокнуть.
Найдите длину пути, на котором мышь намокнет меньше всего. Мышь может менять направление бега, но её скорость постоянна, и под душем двух поливалок мышь мокнет вдвое быстрее.
Источники:
Подсказка 1
Давайте инвертируем путь мышки (т.е. представим, что мышка наоборот выбегает из норы). Очевидно, что ответ от этого никак не поменяется, а решать задачу будет проще. Хорошо, тогда часть своего пути мышь пробежит под двумя поливалками, а другую часть — только под одной.
Подсказка 2
Давайте попробуем чем-нибудь параметризировать траекторию, по которой бежит мышка. Ага! Мы можем задать траекторию бега мышки единственной точкой — точкой, в которой мышь выбегает из зоны двух поливалок. Назовём эту точку H. До (⋅) H мышке выгодней бежать по прямой, а дальше по радиусу одной из окружностей.
Подсказка 3
Пусть (⋅)A и (⋅)B — центры окружностей. Очевидно, что положение (⋅)H определяется углом ∠HAB, а также через этот угол и радиусы окружностей можно записать функцию, описывающую расстояние, которое пробежит мышка!
Подсказка 4
Запишем эту функцию, затем возьмём её производную и найдём локальный экстремум. Также не забываем, в каком диапазоне у нас может меняться ∠HAB! Проверим, что мы нашли именно минимум и найдём соответствующее ему расстояние.
Пусть радиус полива равен 
В точках 
и 
расположены поливалки, нора находится в 
Поменяем направление — пусть
мышь выбегает из норы и стремится на сухую землю. Путь мыши может быть какой угодно формы, но, так или иначе,
ей придётся покинуть область двойного полива — пусть это произойдёт в точке 
Тогда оптимальный путь до точки
— это отрезок 
а оптимальный путь от 
до сухой земли — это 
где 
лежит на радиусе 
Значит,
кандидаты на оптимальный путь — ломаные вида 
и определяются они одним параметром — положением точки 
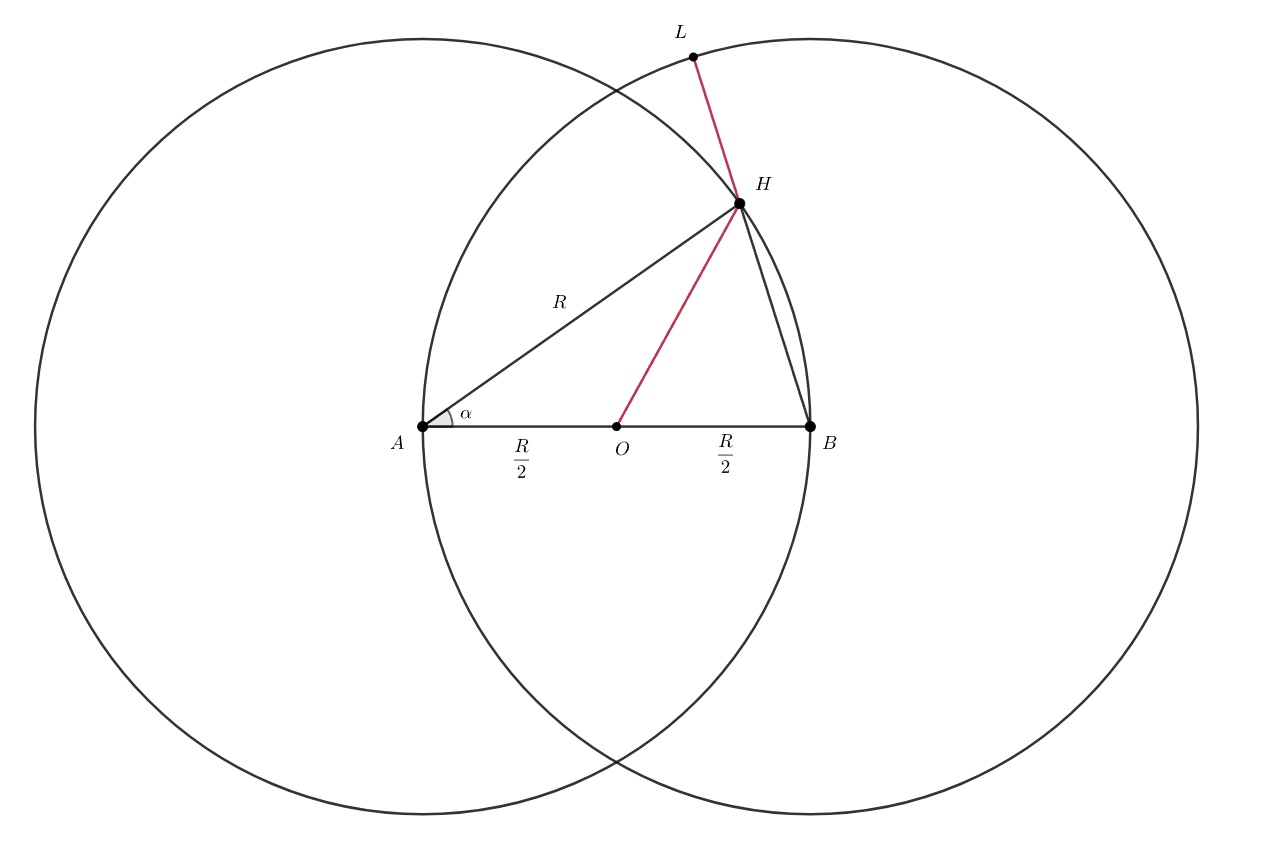
Мышь мокнет от каждой поливалки, поэтому нужно минимизировать сумму расстояний, пройденных под каждой поливалкой. Путь под
поливалкой 
равен 
путь под поливалкой 
равен 
поэтому нужно найти минимально возможное значение
Опишем положение 
через угол 
где ![α ∈[0,60∘].](/api/latex-service/v1/GetSession/259618/index-9b212453ed01217627f03873ea7bb14d.svg)
Тогда:
По теореме косинусов:
Далее, 
а 
найдём как основание равнобедренного треугольника с боковыми сторонами 
и известным углом
между ними:
Значит:
![( ∘ ------- )
2|OH |+|HL|= f(α )=R 2 5− cosα +1− 2sin α-, где α∈ [0,π]
4 2 3](/api/latex-service/v1/GetSession/259618/index-95d11a7d3134b4b1fa247445bf8e3d3a.svg)
Нужно найти минимум функции 
которая характеризует степень намокания — берём производную:
Нулю может равняться только скобка (угол 
меняется в таких пределах, что 
в ноль не обращается). Решаем
уравнение:
Если 
то 
Значит, экстремум 
равен:
На всякий случай проверим, точно ли это точка минимума. Если бы мышь взяла курс ровно наверх, то 
приняла бы значение
что больше, чем 
Если бы побежала направо — 
равнялось бы 
Так что мы действительно нашли
минимум.
Длина пути при этом равна:
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
