Планиметрия на Ломоносове
Ошибка.
Попробуйте повторить позже
Живописец закрасил акварелью полумесяц на клетчатой бумаге. Контур полумесяца состоит из двух дуг — одна от окружности с центром в
, проходящей через 
, другая — от окружности с центром в 
, проходящей через 
. К утру краска расплылась так, что
каждая точка полумесяца превратилась в круг радиуса 
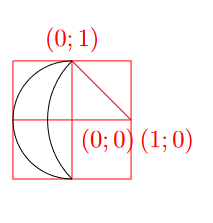
Найдите площадь получившейся фигуры.
Источники:
Пусть рисунок расплылся на радиус 
. К площади полумесяца прибавятся «поля», которые можно разбить на левое, правое и два
закругления на концах рогов.
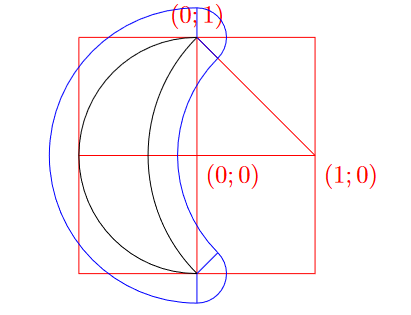
Площадь полумесяца равна половине площади круга радиуса 
минус сегмент круга радиуса 
Площадь левого поля ”— половина от площади кольца с радиусами 
и 
:
Площадь правого поля ”— четверть от площади кольца с радиусами 
и 
:
Закругления на концах рогов вместе составляют три четверти окружности радиуса 
:
Вместе получается:
И тогда ответ:
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
