Стереометрия на Ломоносове
Ошибка.
Попробуйте повторить позже
В правильную треугольную призму вписан шар радиуса
. Найдите площадь боковой поверхности вписанного в шар
прямого кругового цилиндра, основание которого лежит в плоскости, проходящей через точку
и середины рёбер
и
Источники:
Подсказка 1
Давайте аккуратно нарисуем рисунок, попробуем выразить радиус основания цилиндра через его высоту и радиус сферы. Обозначим за D, D₁, M и N середины ребер ВС, В₁С₁, ВВ₁ и СС₁, Р – точка пересечения MN и DD₁. Как имеющиеся на рисунке отрезки связаны с радиусом сферы?
Подсказка 2
Давайте спроецируем центр сферы на плоскость основания цилиндра, нельзя ли теперь выделить на рисунке какую-нибудь пару подобных треугольников, которая поможет нам связать высоту цилиндра и радиус сферы?
Обозначим через радиус шара, а через
и
— середины рёбер
и
соответственно. Плоскость
есть центральное сечение шара. Пусть
— высота цилиндра, тогда радиус его основания равен
. Пусть
— точка
пересечения отрезков
и
.
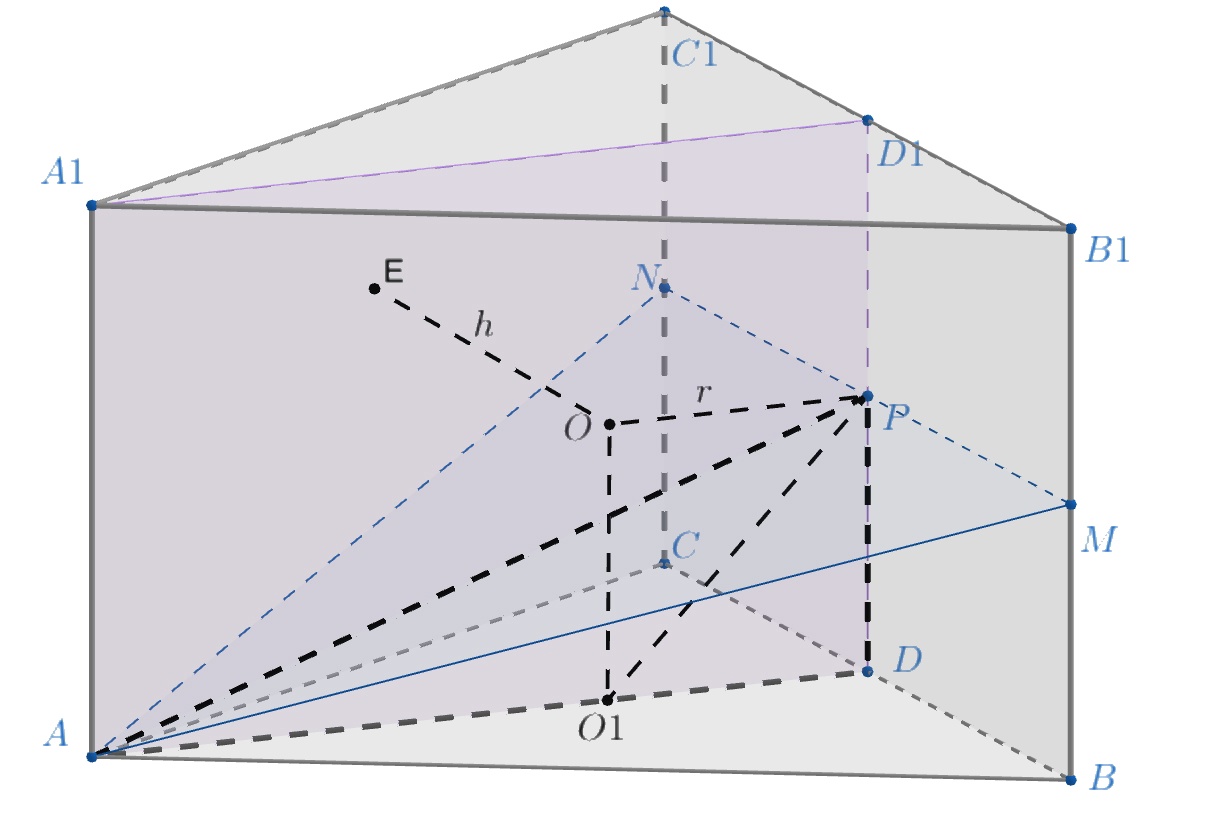
Справедливы соотношения , где
— центр шара. Если
— проекция точки
на основание цилиндра, то
из подобия прямоугольных треугольников
и
получаем
Тогда
Значит, . Площадь боковой поверхности
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




