Стереометрия на Ломоносове

Для отслеживания движения жучка будем использовать частичную развертку куба, покрывающую грани. Каждый квадратик будем обозначать двузначным числом, 1-я и 2-я цифры которого являются соответствующими координатами центра квадратика на развертке (единица — ширина квадратика):

Маршрут жучка определяется его начальным положением и направлением его первого перемещения. Хотя всего таких вариантов их все можно разбить на принципиально различных групп:

1) Жучок стартует с центрального квадратика любой грани по направлению к любому ребру

2-3) Старт с углового квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка

4-5) Старт с углового квадратика любой грани, а при первом перемещении жучок переползает на соседнюю грань, причем третья примыкающая грань остается соответственно справа или слева от него

6) Старт с приреберного квадратика любой грани по направлению к центру

7) Старт с приреберного квадратика любой грани с переходом на соседнюю грань при первом перемещении

8-9) Старт с приреберного квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка

Заполним таблицу, в которой для каждой группы приведем пример маршрута в течение того времени, когда обнаруживается его периодичность, т.е. когда на какой-либо четной секунде жучок оказывается на начальном квадратике, а еще через с — на квадратике, где он был через с после начала движения.

В случае группы выберем для старта квадратик с первым перемещением и проследим весь маршрут, пока не обнаружим, что его период равен c (1-я колонка таблицы после двойной вертикальной черты).

Заметим, что через c после начала движения жучок окажется в начальном состоянии группы Поэтому для нее маршрут также будет иметь период с и его можно получить из маршрута группы сдвигом на с.

Еще через с жучок окажется в начальном состоянии группы Поэтому и для нее маршрут будет с периодом с и его можно получить из маршрута группы сдвигом на с.

Еще через с имеем начальное состояние группы и получаем ее маршрут с периодом с из маршрута группы сдвигом на с.

Для остальных групп получаются кольцевые маршруты с периодом с, причем в течение одного периода жучок ни на одном квадратике не оказывается дважды.

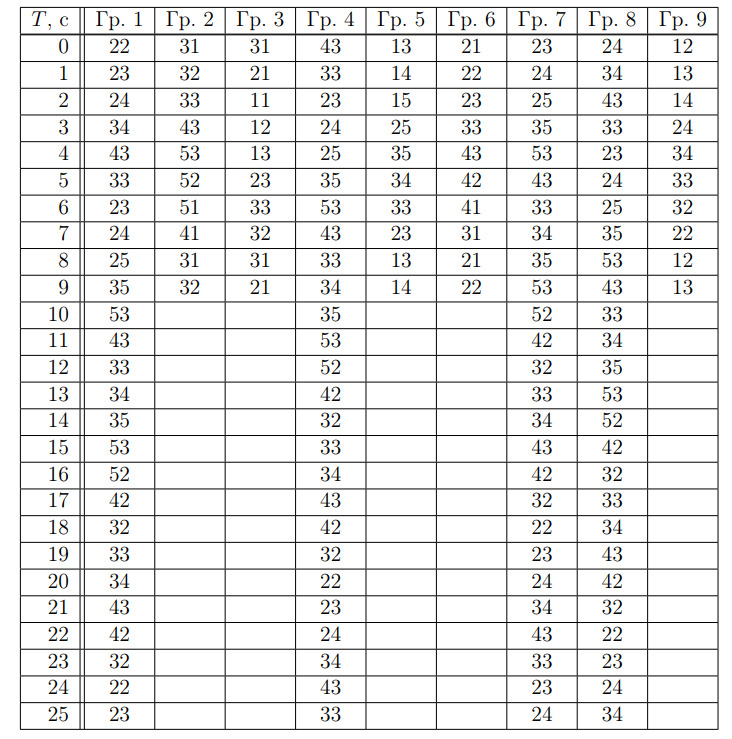
Так как (остаток от деления на равен ) и (остаток от деления на равен то через с после начала движения жучок окажется на том же квадратике, на котором он был через с после начала, а за с до этого — на том же квадратике, на котором он был через с после начала.

Как видно из таблицы, такое совпадение имеет место только для группы (квадратик Так как этот квадратик встречается на маршруте только дважды в течение периода ( с и с), следующее попадание на него произойдет через (с).