Тема Ломоносов

Стереометрия на Ломоносове

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ломоносов

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#67943

На подвешенном воздухе кубике Рубика, на одном из его $54$ квадратиков, сидит жучок. В какой-то момент он начинает движение по поверхности куба, передвигаясь за каждую секунду на соседний квадратик, т.е. на квадратик, имеющий общую сторону с текущим. Соседний квадратик для первого перемещения был выбран произвольно, а затем жучок следовал таким правилам:

1) при 2-м, 4-м и других чётных перемещениях жучок не менял направления своего движения, т.е. покидал квадратик через сторону, противоположную той, через которую он на этот квадратик попал;

2) при 3-м, 5-м и других нечётных перемещениях жучок поворачивал направо (относительно своего движения).

Через 2023 секунды после начала движения жучок обратил внимание на то, что уже был на этом же квадратике 5 секунд назад. Через какое наименьшее число секунд после 2023-й жучок опять окажется на этом квадратике?

Источники: Ломоносов-2023, 10.7 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Заметим, что квадратиков ну ооочень много, но ведь многие из них очень похожи?… Если взять конкретный квадратик, то несложно отследить его путь, т.к путь у жучка определяется начальным положением и направлением. Что тогда попробуем сделать?

Показать ответ и решение

Для отслеживания движения жучка будем использовать частичную развертку куба, покрывающую $3$ грани. Каждый квадратик будем обозначать двузначным числом, 1-я и 2-я цифры которого являются соответствующими координатами центра квадратика на развертке (единица — ширина квадратика):

$PIC$

Маршрут жучка определяется его начальным положением и направлением его первого перемещения. Хотя всего таких вариантов $54× 4,$ их все можно разбить на $9$ принципиально различных групп:

1) Жучок стартует с центрального квадратика любой грани по направлению к любому ребру

2-3) Старт с углового квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка

4-5) Старт с углового квадратика любой грани, а при первом перемещении жучок переползает на соседнюю грань, причем третья примыкающая грань остается соответственно справа или слева от него

6) Старт с приреберного квадратика любой грани по направлению к центру

7) Старт с приреберного квадратика любой грани с переходом на соседнюю грань при первом перемещении

8-9) Старт с приреберного квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка

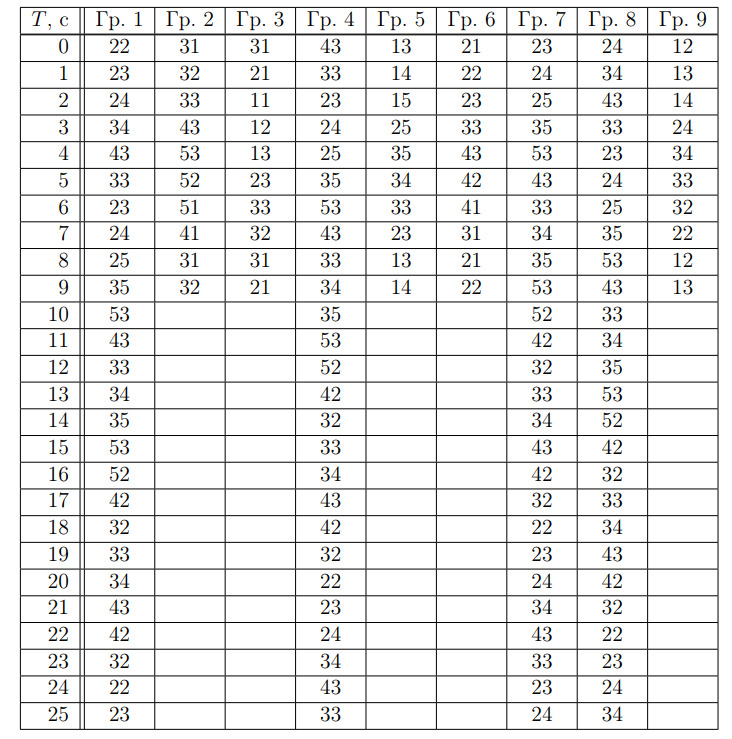
Заполним таблицу, в которой для каждой группы приведем пример маршрута в течение того времени, когда обнаруживается его периодичность, т.е. когда на какой-либо четной секунде жучок оказывается на начальном квадратике, а еще через $1$ с — на квадратике, где он был через $1$ с после начала движения.

В случае группы $1$ выберем для старта квадратик $22$ с первым перемещением $22−→ 23$ и проследим весь маршрут, пока не обнаружим, что его период равен $24$ c (1-я колонка таблицы после двойной вертикальной черты).

Заметим, что через $2$ c после начала движения жучок окажется в начальном состоянии группы $8.$ Поэтому для нее маршрут также будет иметь период $24$ с и его можно получить из маршрута группы $1$ сдвигом на $2$ с.

Еще через $2$ с жучок окажется в начальном состоянии группы $4.$ Поэтому и для нее маршрут будет с периодом $24$ с и его можно получить из маршрута группы $1$ сдвигом на $4$ с.

Еще через $2$ с имеем начальное состояние группы $7$ и получаем ее маршрут с периодом $24$ с из маршрута группы $1$ сдвигом на $6$ с.

Для остальных групп получаются кольцевые маршруты с периодом $8$ с, причем в течение одного периода жучок ни на одном квадратике не оказывается дважды.

$PIC$

Так как $2023≡ 7 mod 24$ (остаток от деления $2023$ на $24$ равен $7$ ) и $2023≡ 7 mod 8$ (остаток от деления $2023$ на $8$ равен $7),$ то через $2023$ с после начала движения жучок окажется на том же квадратике, на котором он был через $7$ с после начала, а за $5$ с до этого — на том же квадратике, на котором он был через $2$ с после начала.

Как видно из таблицы, такое совпадение имеет место только для группы $1$ (квадратик $24).$ Так как этот квадратик встречается на маршруте только дважды в течение периода ( $2$ с и $7$ с), следующее попадание на него произойдет через $2+ 24− 7= 19$ (с).

Ответ: 19

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#70490

Угол при вершине в осевом сечении конуса равен $60∘$ . Снаружи этого конуса расположены 11 шаров радиуса 3, каждый из которых касается двух соседних шаров, боковой поверхности конуса и плоскости его основания. Найдите радиус основания конуса.

Источники: Ломоносов-2022, 11.4 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте сначала рассмотрим расположение любого шара и конуса в плоскости, перпендикулярной рисунку.

Подсказка 2

У нас есть треугольник, которого касается окружность известного радиуса, вписанная во внешний угол при основании треугольника. Счёт за Вами... Напоминаем, окружность, вписанная в угол, лежит на его биссектрисе

Подсказка 3

Теперь давайте поймем как расположены все шары снаружи. Они касаются друг друга, поверхности конуса и плоскости его основания, причем все расположены на одинаковом расстоянии от центра основания конуса!

Подсказка 4

То есть точки касания шаров с плоскостью основания конуса являются вершина правильного 11-угольника со стороной, равной удвоенному радиусу шаров(так как они касаются друг друга и длина = 2 радиуса)...

Подсказка 5

Теперь нам известны расстояние от центра основания до точки касания шаров с плоскостью основания(радиус 11-угольника) и расстояние от этой точки касания до ближайшей вершины треугольника в плоскости рисунка, тогда искомый радиус основания = радиус 11-угольника - последнее расстояние

Показать ответ и решение

$PIC$

Пусть $O$ — центр окружности основания конуса, радиуса $R,Q1$ - центр одного из шаров радиуса $3,H1$ — точка касания этого шара с плоскостью основания, $H2$ — точка касания соседнего шара с плоскостью основания конуса. Значит, из треугольника $AQ1H1$ можем получить

AH1 =--(-Q1H1-∘) = 3√--=√3 tg 45∘+ 302-- 3

$PIC$

Так как каждый шар касается двух соседних, то точки касания этих шаров с плоскостью основания конуса расположены в вершинах правильного 11-угольника вписанного в окружность с центром в точке $O,$ радиуса $OH1$ и стороной, равной $2⋅3= 6.$ Поэтому

180∘- Q1H =OH1 sin 11 , где OH1 = R+ AH1

Q1H 3 √- R = sin180∘-− AH1 = sin-180∘− 3 11 11

Ответ:

$---3--− √3 sin 18101∘$

Ошибка.
Попробуйте повторить позже

Задача 3#92158

В неправильной пирамиде $ABCD$ сумма плоских углов при вершине $A$ равна $180∘$ . Найдите площадь поверхности этой пирамиды, если площадь грани $BCD$ равна $s$ и $AB = CD,AD = BC.$

Источники: Ломоносов - 2021, 11.6 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Дана пирамида и некие условия на неё, которые касаются углов и сторон. А вычислить нужно площадь поверхности, то есть "плоскую" характеристику. Что тогда можно сделать, чтобы упростить себе восприятие задачи?

Подсказка 2

Естественное желание при решении почти любой стереометрической задачи — свести её к задаче по планиметрии. Здесь, поскольку речь идёт о сторонах, плоских углах и площадях, будет удобно рассмотреть развёртку пирамиды. Воспользуемся же всеми условиями задачи на развёртке!

Подсказка 3

Теперь наглядно можно увидеть, что мы имеем 4 треугольника, кучу равных отрезков и 3 угла при вершине А, составляющие в сумме развёрнутый. Что хочется доказать про эти треугольники?

Подсказка 4

Конечно, хочется доказать, что все 4 треугольника равны между собой. Воспользуемся признаками равенства треугольников и параллельностью!

Показать ответ и решение

Докажем, что грани пирамиды — равные треугольники. Для этого рассмотрим развёртку $AD ′′′BD ′CD ′′$ пирамиды $ABCD$ , где

′′ ′′′ ′′′ ′ ′′ ′ AD =AD =AD, BD = BD =BD, CD =CD = CD

$PIC$

Пусть $∠BAC = α,∠BAD ′′′ = β,∠CAD′′ = γ$ . Так как $α+ β+ γ = 180∘$ , то точки $D ′′,A,D ′′′$ лежат на одной прямой. Так как $AD ′′ = BC,AB = D′′C$ , то $ABCD ′′$ — параллелограмм и $BC ∥AD′′$ . Аналогично $AD′′′BC$ — тоже параллелограмм. Треугольник $ACD ′′$ равен треугольнику $BCD ′$ . Значит, грани пирамиды — равные треугольники.

Ответ:

$4s$

Ошибка.
Попробуйте повторить позже

Задача 4#63893

Отрезок $AB = 8$ пересекает плоскость $α$ под углом $30∘$ и делится этой плоскостью в отношении $1:3$ . Найдите радиус сферы, проходящей через точки $A$ и $B$ и пересекающей плоскость $α$ по окружности наименьшего радиуса.

Источники: Ломоносов-2015, 11.5 (см. olymp.msu.ru)

Показать ответ и решение

Обозначив точку пересечения $AB$ с плоскостью $α$ через $C$ , получим $AC =2,BC = 6$ . В пересечении сферы с плоскостью получается некоторая окружность. Проведём через $C$ диаметр $MN$ этой окружности.

$PIC$

Тогда $AB$ и $MN$ — хорды сферы, и по свойству пересекающихся хорд: $MC ⋅CN = AC ⋅CB = 12$ . Так как $------- - MN = MC + CN ≥2√MC ⋅CN =4√ 3$ , то минимальный радиус окружности больше или равен $- 2√3$ и значение $- 2√ 3$ достигается при $MC =CN =2√3$ , то есть $C−$ центр этой окружности. Так как $∠COP = 90∘− ∠OCP = ∠NCP = 30∘$ , то $OC =2⋅CP.$ При этом $CP = AB2-− AC = 2.$ Значит, $R2 =OM2 =MC2 + OC2 = 12 +42 = 28.$

Ответ:

$2√7$

Ошибка.
Попробуйте повторить позже

Задача 5#63895

В правильную треугольную призму $ABCA B C 1 1 1$ вписан шар радиуса $√2$ . Найдите площадь боковой поверхности вписанного в шар прямого кругового цилиндра, основание которого лежит в плоскости, проходящей через точку $A$ и середины рёбер $BB1$ и $CC1.$

Источники: Ломоносов-2014, 11.7 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте аккуратно нарисуем рисунок, попробуем выразить радиус основания цилиндра через его высоту и радиус сферы. Обозначим за D, D₁, M и N середины ребер ВС, В₁С₁, ВВ₁ и СС₁, Р – точка пересечения MN и DD₁. Как имеющиеся на рисунке отрезки связаны с радиусом сферы?

Подсказка 2

Давайте спроецируем центр сферы на плоскость основания цилиндра, нельзя ли теперь выделить на рисунке какую-нибудь пару подобных треугольников, которая поможет нам связать высоту цилиндра и радиус сферы?

Показать ответ и решение

Обозначим через $r$ радиус шара, а через $D,D ,M 1$ и $N$ — середины рёбер $BC,B C ,BB 11 1$ и $CC 1$ соответственно. Плоскость $AA D 1 1$ есть центральное сечение шара. Пусть $h$ — высота цилиндра, тогда радиус его основания равен $∘-2--h2 R = r − 4$ . Пусть $P$ — точка пересечения отрезков $DD1$ и $MN$ . Справедливы соотношения $OP = r,P D= r,AD =3r$ , где $O−$ центр шара. Если $O1$ — проекция точки $O$ на основание цилиндра, то из подобия прямоугольных треугольников $APD$ и $OO1P$ получаем

OO1 PD -OP-= AP-

OOr1-= √--r2--2-= √1- 9r + r 10

Тогда

√ -- √-- OO = r-10,h =2 ⋅OO = r-10 1 10 1 5

Значит, $R= 3r√10 10$ . Площадь боковой поверхности

6πr2 Sбок. = 2πRh= 5

Ответ:

$12π 5$

Ошибка.
Попробуйте повторить позже

Задача 6#90596

На ребре $AS$ треугольной пирамиды $SABC$ отмечены такие точки $M$ и $N$ , что $AM = MN =NS$ . Найдите площадь треугольника $NBC$ , если площади треугольников $ABC,MBC$ и $SBC$ равны 2, 1 и $√- 2 7$ соответственно.

Показать ответ и решение

Пусть $S = 1,S = 2,S ,S = √37 1 2 3 4$ — площади треугольников $ABC, MBC, NBC,SBC$ соответственно, а $h ,h,h ,h 1 2 3 4$ — их высоты, опущенные на общее основание $BC :$

$PIC$

Обозначим через $A′$ , $B′,C′,S′,M ′,N′$ ортогональные проекции точек $A,B,C$ , $S,M,N$ соответственно на некоторую плоскость, перпендикулярную ребру $BC :$

$PIC$

Точки $′ B$ и $′ C$ совпадают, причём

′ ′ ′ ′ ′′ A M = M N =N S = a A′B′ = h1, M′B′ = h2, N′B′ = h3, S′B ′ =h4

Учитывая, что $′ ′ M B$ и $′′ N B$ — медианы треугольников $′ ′ ′ A BN$ и $′ ′′ M BS$ , имеем

2 2 2 2 2 2 2 h1+ h3 − 2h2 = 2a = h2 +h4− 2h3 ⇒ ∘ ---------- 2 2 2 2 2 h24-− h21 ⇒ 3h3 = 3h2+ h4− h1 ⇒ h3 = h2 + 3

А так как площади $S1,S2,S3,S4$ пропорциональны высотам $h1,h2$ , $h3,h4$ с коэффициентом $k= BC2-$ , получаем

∘-----------2------2 ∘ -----2---2- ∘-------- S3 = kh3 = (kh2)2+ (kh4)-−3-(kh1)-= S22 + S4 −3 S1-= 4+ 37−3-1= 4

Ответ: 4

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#72980

В треугольной пирамиде $SABC$ ребро $SA$ перпендикулярно плоскости $ABC,∠SCB = 90∘,BC = √5,AC =√7-$ . Последовательность точек $On$ строится следующим образом: точка $O1$ — центр сферы, описанной около пирамиды $SABC$ , и для каждого натурального $n ≥2$ точка $On$ есть центр сферы, описанной около пирамиды $On−1ABC$ . Какую длину должно иметь ребро $SA$ , чтобы множество ${On}$ состояло ровно из двух различных точек?

Подсказки к задаче

Подсказка 1

Т.к. SA ⊥ (ABC), то угол ∠SAB=90⁰. По условию ∠SCB=90⁰. Это означает, что наши точки лежат на сфере, с диаметром SB. А на какой прямой лежат центры O₁, O₂, ...?

Подсказка 2

Правильно, на перпендикуляре к плоскости (ABC), проведенной в точке X- середине AB. Мы хотим, чтобы множество наших центров состояло всего из двух точек. Давайте тогда поймем, когда O₃ совпадает с кем-то из O₁, O₂.

Подсказка 3

Ясно, что с O₂ она совпадать не может. Т.к. O₁- середина SB, то и O₃- середина SB. Т.к. O₃ равноудалена от A, B, C и O₂, а O₂ равноудалена от A, B, C и O₁=O₃, то AO₃BO₂- ромб с углом 60°. Я думаю, что вы сможете закончить решение!

Показать ответ и решение

$PIC$

Применим теорему о трех перпендикулярах. В силу того, что $SA ⊥ (ABC )$ и $SC ⊥ BC$ , получим, что проекция $SC$ на плоскость $(ABC )$ перпендикулярна $BC$ , то есть $AC ⊥ BC.$

Заметим, что середина гипотенузы $AB$ - точка $X$ это центр описанной окружности прямоугольного треугольника $△ACB$ . Аналогично середина гипотенузы $SB$ - точка $Y$ - центр описанной окружности прямоугольного треугольника $△SAB$ . Тогда если провести перпендикуляр к плоскости $(ABC )$ в точке $X$ и перпендикуляр к плоскости $(SAB)$ в точке $Y$ , то центр описанной окружности $O1$ пирамиды $SABC$ - точка пересечения этих перпендикуляров. Но перпендикуляр к плоскости $(ABC )$ в точке $X$ совпадает с прямой $XY$ . То есть точка $O1$ и есть точка $Y$ .

При этом на прямой $XY$ (перпендикуляр к плоскости $(ABC )$ в точке $X$ ) будут лежать все $On$ в силу того, что $XY$ - ГМТ точек равноудаленных от $A,B,C.$

То есть точка $O2$ - центр треугольной пирамиды $O1ABC$ - опять-таки должна лежать на прямой $XY.$

$PIC$

Хотелось бы добиться того, чтобы $O3 = O1$ ( $O3 ⁄=O2$ по очевидным причинам). Но тогда $O3 = Y$ . То есть середина гипотенузы $△SAB$ равноудалена от точек $A,B,O2$ . Так же точка $O2$ равноудалена от точек $A,B,Y$ . Но тогда $AY BO2$ должен быть ромбом, при этом его диагональ $YO 2$ должна быть равна стороне. Понятно, что тогда $∠AY B = 120∘$ . Значит, что $∠SBA = 30∘$ , то есть $SA = tan30∘⋅AB = 1√-⋅√AC2-+-BC2 = √1√2-=2. 3 3$

Ответ:

$2$

Ошибка.
Попробуйте повторить позже

Задача 8#91918

Основанием пирамиды служит треугольник со сторонами 5, 12 и 13, а её высота образует с высотами боковых граней (опущенными из той же вершины) одинаковые углы, не меньшие $∘ 30.$ Какой наибольший объём может иметь такая пирамида?

Показать ответ и решение

Пусть $A 1$ , $B 1$ и $C 1$ — основания перпендикуляров, опущенных из основания $O$ высоты $DO$ пирамиды $ABCD$ на стороны соответственно $BC$ , $AC$ и $AB$ основания $△ABC$ , причём $BC =12$ , $AC = 5$ , $AB =13$ .

$PIC$

По теореме о трёх перпендикулярах $DB1 ⊥AC$ , $DC1 ⊥ AB$ и $DA1 ⊥ BC$ . Значит, $DB1$ , $DC1$ и $DA1$ — высоты боковых граней пирамиды. По условию задачи $∠ODB1$ = $∠ODC1$ = $∠ODA1$ . Прямоугольные треугольники $ODB1$ , $ODC1$ и $ODA1$ равны по катету и прилежащему острому углу, значит, $OB1 =OC1 = OA1$ , то есть точка $O$ равноудалена от прямых, на которых лежат стороны треугольника $ABC$ . Следовательно, $O$ – либо центр вписанной окружности этого треугольника, либо центр его вневписанной окружности. Обозначим $∠ODB1 = ∠ODC1 = ∠ODA1 = α≥ 30∘$ . Заметим, что треугольник $ABC$ —прямоугольный ( $AC2 +BC2 = 25+ 144= 169= 132 =AB2$ ), причём $∠ACB =90∘$ . Пусть $r$ — радиус его вписанной окружности, а $ra$ , $rb$ и $rc$ — радиусы вневписанных окружностей, касающихся сторон $BC$ , $AC$ и $AB$ соответственно, $S$ – площадь треугольника $ABC$ , $p$ – его полупериметр. Тогда

S = 1AC ⋅BC = 30 2

1 S- p= 2(AB +BC + AC)= 15,r= p = 2

S S S ra = p-− BC-= 10,rb = p−-AC-= 3,rc = p−-BA-= 15

Если $h$ , $ha$ , $hb$ и $hc$ — высоты пирамиды соответствующей каждому из рассмотренных случаев, то

h= rctgα,ha = ractgα,hb = rbctgα,hc = rcctgα.

Поскольку в каждом из этих случаев площадь основания пирамиды одна и та же, объём пирамиды максимален, если максимальна её высота. В свою очередь, максимальная высота соответствует максимальному из найденных четырёх радиусов, то есть $rc = 15$ . Поэтому