Стереометрия на СПБГУ
Ошибка.
Попробуйте повторить позже
Две правильные треугольные пирамиды имеют общую боковую грань и не имеют других общих точек. В пирамиды вписаны шары радиуса
Третий шар радиуса
касается внешним образом обеих пирамид и вписанных в них шаров. Найдите плоский угол при вершине
пирамид, если
Источники:
Подсказка 1
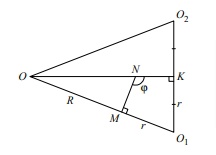
Пусть O₁ и O₂ - центры вписанных сфер, а O — центр внешней сферы. Рассмотрите треугольник OO₁O₂, из него можно получить много информации.
Подсказка 2
Ну, во-первых, он равнобедренный. Во-вторых, вы можете выразить его стороны через радиусы. В-третьих, попробуйте рассмотреть точки K — середину O₁O₂, M — точка касания сферы и одной из пирамид и точку N касания вписанных сфер. Что можно сказать про угол MNK и чему он равен?
Подсказка 3
Это угол между боковыми гранями пирамиды. Кстати, почему? Пусть боковое ребро пирамиды равно a. Используя величину угла, вы сможете выразить длину ребра основания через a, если проведёте высоты в двух боковых гранях к одному ребру. А там и до плоского угла при вершине недалеко.
Пусть — первая пирамида,
— её общая боковая грань со второй,
и
— центры шаров, вписанных в пирамиды,
—
центр внешнего шара. Ввиду равенства пирамид вписанные в них шары касаются грани
в одной точке
Так как
и
точка
лежит на отрезке
причём
Пусть — точка касания с гранью
шара, вписанного в первую пирамиду. В этой же точке касается
и внешний шар.
Поэтому точка
лежит на отрезке
причём
Аналогично получается, что
Выберем точку
на
отрезке
так, что
и положим
Тогда
По условию откуда
Покажем, что — угол между гранями
и
Действительно,
и
— радиусы шара, вписанного в первую пирамиду,
откуда
и
Значит,
Кроме того, прямая
лежит в плоскости
, а
— в плоскости
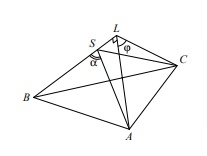
Пусть Опустим из точек
и
перпендикуляры на ребро
Они придут в одну точку
так как
треугольники
и
равны. По доказанному
Заметим, что
Тогда по теореме косинусов для треугольника
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




