Планиметрия на Росатоме
Ошибка.
Попробуйте повторить позже
Трапеция с прямым углом при вершине
описана около окружности. Ее диагонали
и
пересекаются в точке
Найти площадь треугольника
если длина стороны
равна 2.
Источники:
Подсказка 1
Пусть AD = a, BC = b, AB = d, O — центр вписанной окружности, её радиус — r. Какие дополнительные построения Вы видите в этой конструкции?
Подсказка 2
А давайте проведём перпендикуляры из O на стороны трапеции.
Подсказка 3
Скажем, что мы получили точки K, L и N на сторонах BC, AD и AB соответственно. Попробуйте порассуждать о параллельных прямых.
Подсказка 4
OL и OK перпендикулярны BC и AD, но BC ∥ AD, тогда точки K, O и L должны лежать на одной прямой.
Подсказка 5
Получается, что ABLK — прямоугольник и KL = AD = d. Что можно сказать о точках касаний окружности?
Подсказка 6
Оказывается, что KL — это диаметр. А какие ещё прямоугольники Вы видите на картинке?
Подсказка 7
Можно увидеть прямоугольники ANOK и NBLO. Давайте для разнообразия подумаем о треугольниках.
Подсказка 8
Например, треугольник AMD подобен треугольнику CMD.
Подсказка 9
А ведь ещё треугольник APM подобен треугольнику CQM. Попробуйте выразить сторону AP.
Подсказка 10
Вспомните, чем является точка O.
Подсказка 11
O — центр вписанной окружности, следовательно, является точкой пересечения биссектрис.
Подсказка 12
Попробуйте, выражая углы, доказать, что треугольники DKO и OLC подобны.
Подсказка 13
Осталось только применить величину AP и посчитать площадь!
Пусть
Пусть
— центр вписанной в трапецию
окружности
радиуса
Пусть
—
основания перпендикуляров из
на стороны трапеции
и
соответственно.
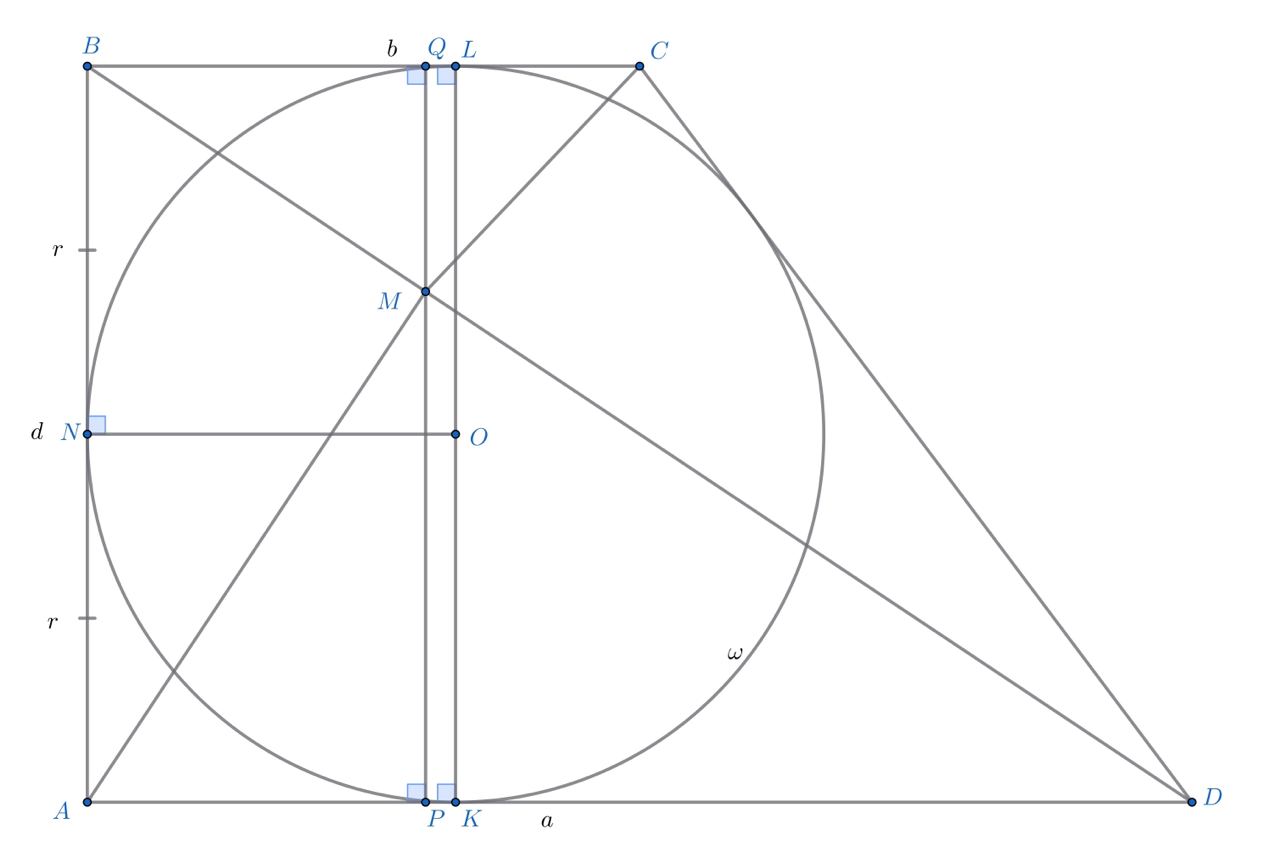
Так как и
перпендикулярны
и
а
то точки
и
лежат на одной прямой, перпендикулярной
и параллельной
Тогда
— прямоугольник и
Заметим, что
и
являются точками касания
окружности
сторон
и
Тогда
— диаметр
и
Аналогично, — прямоугольник и
— прямоугольник и
— прямоугольник и
Заметим, что треугольник подобен треугольнику
по двум углам
с
коэффициентом подобия
Кроме того, треугольник подобен треугольнику
по двум углам
с
коэффициентом подобия
Следовательно,
Получим, что
Так как — центр вписанной в трапецию
окружности, то он лежит на пересечении биссектрис углов трапеции. Тогда
и
— биссектрисы
и
соответственно.
Следовательно, в треугольнике
Тогда треугольник подобен треугольнику
по двум углам
и их стороны пропорциональны:
Таким образом, и точки
лежат на одном перпендикуляре к основаниям трапеции. Тогда длина перпендикуляра из
на
равна
Найдем площадь треугольника с помощью основания
и высоты из
на
равной
1
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




