Тема Росатом

Планиметрия на Росатоме

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела росатом

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#76941

Длина стороны $AD$ четырехугольника $ABCD$ вписанного в окружность равна 5 . Точка $M$ делит эту сторону в отношении $AM :MD = 1:4$ , а прямые $MC$ и $MB$ параллельны сторонам $AB$ и $CD$ соответственно. Найти длину стороны $BC$ четырехугольника.

Источники: Росатом - 2024, московский вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Сразу обозначим все углы, вытекающие из параллельности. Как использовать отношение, данное в условии? Какую связь можно заметить между треугольниками на картинке?

Подсказка 2

Треугольники ABM и MCD подобны с коэффициентом 4. О равенстве каких углов теперь можно утверждать? Что хочется сказать о треугольнике BMC? Какое условие мы еще не использовали?

Подсказка 3

Докажем, что треугольник BMC подобен ABM и MCD. Помним, что четырехугольник вписан.

Подсказка 4

Теперь при помощи трех попарно подобных треугольников мы можем найти связь нужной нам BC и известной AD. Было бы удобно найти коэффициент подобия BAM и MBC…Как это сделать?

Подсказка 5

Обозначим стороны треугольника BAM через переменные. Остаётся лишь записать цепочку равенств! В этом нам может помочь данное в условии отношение)

Показать ответ и решение

$PIC$

Прямые $MB$ и $CD$ параллельны, поэтому углы $BMA$ и $CDA$ равны (обозначены на рисунке цифрой 2 ), аналогично равны углы $BAM$ и $CMD$ (обозначены на рисунке цифрой 3). Отсюда следует подобие треугольников $BAM$ и $CMD$ с коэффициентом подобия 4 и равенство углов $ABM$ и $MCD$ (обозначены на рисунке цифрой 1). Заметим, что $ˆ1 +ˆ2+ ˆ3= π$ .

Покажем, что треугольник $MBC$ подобен треугольникам $BAM$ и $CMD$ , вершины треугольников перечислены в порядке соответствия. Углы $DCM$ и $BMC$ , полученные при пересечении прямой $CM$ параллельными прямыми $MB$ и $CD$ , равны как внутренние накрест лежащие. Сумма углов $BCD = BCM + ˆ1$ и $BAD = ^3$ равна $π$ , как сумма противоположных углов вписанного в окружность четырёхугольника. Значит, угол $BCM = ˆ2$ и треугольник $MBC$ подобен треугольникам $BAM$ и $CMD$ .

Положим $p:= BA$ и $q :=BM$ , тогда $CM =4p$ и $CD = 4q$ . Треугольники $BAM$ и $MBC$ подобны с коэффициентом подобия $pq$ , и стороны $BA$ и $BM$ треугольника $BAM$ соответствуют сторонам $MB$ и $MC$ треугольника $MBC$ , поэтому $pq =4qp$ . Значит, $q =2p$ и, треугольники $BAM$ и $MBC$ подобны с коэффициентом подобия 2. Следовательно, сторона $BC$ в два раза длиннее стороны $AM$ , т.е. длина стороны $BC$ равна 2.

Ответ: 2

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#46042

На сторонах $AB$ и $AC$ остроугольного треугольника $ABC$ вовне построены два равных прямоугольника $AMNB$ и $APQC$ . Найдите расстояние между вершинами $N$ и $Q$ прямоугольников, если длины сторон $AB$ и $AC$ равны $3$ и $4$ соответственно, а угол при вершине $A$ треугольника равен $∘ 30$ .

Источники: Росатом-20, 11.6 (см. mephi.ru)

Подсказки к задаче

Подсказка 1

Видим, что искомый нами отрезок находится в треугольнике NAQ. А если бы мы знали две стороны и угол этого треугольника, как мы решали задачу?

Подсказка 2

Верно, тогда бы мы просто нашли сторону по теореме косинусов! Давайте же попробуем найти все неизвестные части. Иногда про угол хорошо думать как о сумме нескольких углов, потому что каждый по отдельности нас не интересует. Можно ли здесь "перекинуть" уголки так, чтобы по итогу мы знали, чему они равны в сумме?

Подсказка 3

Ага, ведь прямоугольники у нас равны, поэтому получается, что в сумме два крайних угла равны 90, а третий кусочек мы знаем из условия. Теперь осталось только понять, что две стороны мы можем найти по теореме Пифагора.

Показать ответ и решение

$PIC$

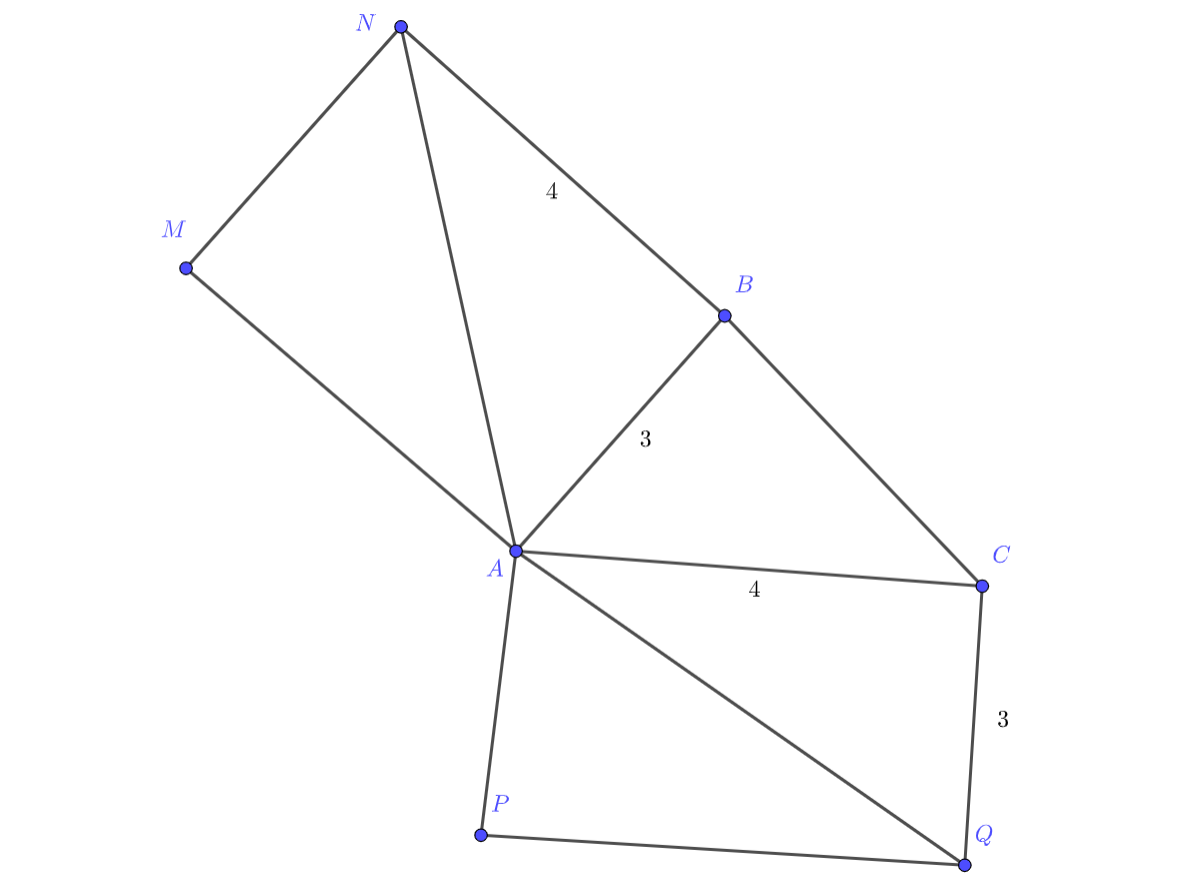
Поскольку прямоугольники равны, то $BN =AC = 4,AB = CQ = 3$ , откуда их диагонали $AQ = AN =5$ . Заметим, что $∠CAQ + ∠BAN =∠CAQ +∠AQC = 90∘$ , откуда $∠NAQ =90∘+ 30∘ = 120∘$ . Тогда из равнобедренного $△ANQ$ легко найти $√- NQ = 5 3$ .

Ответ:

$5√3$

Ошибка.
Попробуйте повторить позже

Задача 3#49010

Точка $M$ — середина стороны $AD$ параллелограмма $ABCD.$ Прямая $CM$ наклонена к основанию $AD$ под углом $30∘$ . Вершина $B$ равноудалена от прямой $CM$ и вершины $A$ . Найти углы параллелограмма. Найти площадь параллелограмма, если длина основания $AD$ равна $2.$

Подсказки к задаче

Подсказка 1

В условии фигурирует расстояние от точки B до CM, поэтому опустим перпендикуляр из B на CM (назовём его BH), чтобы с этим как-то работать. Обозначим данный нам угол в 30 градусов, попробуем как-то поработать с параллельностью и углами.

Подсказка 2

Отметив ещё один угол в 30 градусов, который возникает из параллельности, находим на картинке прямоугольный треугольник с углом в 30 градусов. Благодаря этому можно связать длину перпендикуляра из B на CM и сторону параллелограмма. Тогда, использовав условие, мы можем связать две стороны параллелограмма, что даёт нам возможность найти его углы (зная, что CM опущен под углом 30 градусов). Как же найти площадь?

Подсказка 3

Благодаря найденным углам мы можем разбить нашу картинку на несколько равных правильных фигур, у каждой из которых найти площадь по формуле не составит труда)

Показать ответ и решение

Первое решение.

$PIC$

Пусть $BH =x.$ Тогда

По условию BH = AB = CD = x;

∠CMD =∠BCH = 30∘ ⇒ в △HBC BC = 2⋅BH = 2x;

BC =AD =2x⇒ AM = MD = x;

Тогда в $△MDC$

∘ ∘ MD =DC = x; ∠CMD = 30 ⇒ ∠MCD =30

Следовательно, $∠BCD = 60∘, ∠CDA = 120∘$

Теперь легко посчитать площадь параллелограмма:

∠BCD = 60∘;CD =1;BC = 2⇒

SABCD =sin(60∘)⋅1⋅2= √3

Второе решение.

$PIC$

Опустим перпендикуляр $BH$ на $CM$ , отметим середину $N$ отрезка $BC$ и обозначим $E$ — точку пересечения $BH$ и $AN$ . Тогда $AB = BH = 2BE$ , так как $AN ∥CM$ и $N$ — середина $BC$ . Тогда треугольник $ABE$ прямоугольный и $AB = 2BE$ . Значит $∠ABE =60∘$ и $∠NAB = 30∘$ . Так же $∠NAM =∠MCD = 30∘$ из параллельности и поэтому $AN$ биссектриса угла $BAM.$ Четырехугольник $ABNM$ является параллелограммом и при этом $AN$ биссектриса угла $BAM$ . Значит $ABNM$ ромб и $BM ⊥ AN$ , но $BH ⊥ AN$ . Значит, $M = H.$

$PIC$

Тогда $AB = AM$ и $∠ABM = 60∘$ . Значит, треугольник $ABM$ равносторонний со стороной $AM = AD2-=1$ . Тогда $SAMB = √34$ , $SABNM = √3 2$ и $SABCD =√3.$

Ответ:

$60∘$

$∘ 120$

$√- 3$

Ошибка.
Попробуйте повторить позже

Задача 4#49011

На сторонах $AB$ и $BC$ треугольника $ABC$ расположены точки $M$ и $N$ так, что $AM =CN =√3-$ . Точка $P$ – середина отрезка $MN$ , точка $Q$ – середина стороны $AC.$ Угол при вершине $B$ треугольника $ABC$ равен $∘ 60.$ Найти длину отрезка $P Q.$

Источники: Росатом-19, 11.6 (см. mephi.ru)

Подсказки к задаче

Подсказка 1

Вспомните, как векторно выразить среднюю линию четырёхугольника

Подсказка 2

Затем вспомните, что длина это корень из скалярного квадрата

Показать доказательство

Первое решение.

Давайте вспомним, что отрезок между серединками каких-то сторон может быть удобно посчитать через векторы:

−−→ −−→ −P−→Q = Q− P = A+-C-− M-+N-= A-−-M + C−-N-= MA-+-NC- 2 2 2 2 2

Тем более нам дан угол между векторами $AM$ и $CN$ — он равен углу между векторами $AB$ и $CB$ (ведь $−A−M→$ сонаправлен $−A→B$ , а $−C−→N$ сонаправлен $−C−→B$ ) то есть $60$ градусам. Осталось вспомнить, что длина связана со скалярным квадратом:

∘------ ∘----- ┌│ (−−→--−−→-)-2 P Q= |−−→PQ|= |−−−P−→Q|= |−−−−P→Q|2 = −−−−P→Q2 = ││∘ (AM-+CN-) 2

Раскрываем квадрат суммы:

(2PQ )2 = −A−→M2 + −−C→N2 +2(−−A→M,−C−→N )= AM2 + CN2+ 2⋅AM ⋅CN ⋅cos∠ (−A−M→, −C−→M )= 3+3 +2⋅3⋅ 1 = 9 2

Отсюда $2PQ =3.$

Второе решение.

$PIC$

Давайте заметим, что если сдвинуть точку $C$ и $N$ по стороне $B$ на вектор $v$ , то условие останется выполненным, а точки $P$ и $Q$ сдвинуться на вектор $v 2$ . Значит длина $PQ$ не измениться. Аналогично, можно сдвинуть точки $A$ и $M$ вдоль $AB$ так, чтобы условие и длина $PQ$ сохранилась. Сдвинем $N$ и $M$ в точку $B$ и получим.

$PIC$

Тогда $P = B$ , $√- AB = AC = 3$ и $∠ABC = 60∘$ . Значит, перед нами равносторонний треугольник и $PQ$ медиана в нем. Значит, ее длина равна $32.$

Ошибка.
Попробуйте повторить позже

Задача 5#68258

Около выпуклого четырехугольника $ABCD$ , диагонали которого перпендикулярны и по длине равны 5 и 6, можно описать окружность с центром в точке $O$ . Найдите площадь четырехугольника $ABCO$ .

Подсказки к задаче

Подсказка 1

Обозначим дуги AB и BC за b и a соответственно. Что мы можем тогда сказать про дуги CD и AD, если мы знаем, что AC и BD перпендикулярны?

Подсказка 2

AB+СD=2*90° и BC+AD=2*90°. Тогда AOB=b, BOC=a, COD=180°-b и AOD=180°-a. Как тогда между собой относятся площади треугольников AOB и COD, если вспомнить, что sin(x)=sin(180°-x)...

Подсказка 3

Они равны, ведь S(AOB)=R*R*sin(b)/2 и S(COD)=R*R*sin(180°-b)/2=R*R*sin(b)/2. Аналогично, равны площади треугольников BOC и AOD. Что мы можем сказать про отношение площадей четырехугольника ABCO и ABCD?

Подсказка 4

S(ABCO) = S(AOB)+S(BOC) и S(ABCD) = S(AOB)+S(BOC)+S(COD)+S(AOD)=2(S(AOB)+S(BOC))=2S(ABCO). Осталось только вспомнить формулу для площади четырехугольника через диагонали и угол между ними и завершить решение.

Показать ответ и решение

$PIC$

Пусть хорды $BC$ и $AB$ стягивают дуги с центральными углами $α$ и $β$ соответственно. Тогда в силу перпендикулярности диагоналей, хорды $AD$ и $CD$ стягивают дуги с центральными углами $180∘− α$ и $180∘− β$ . То есть имеем

∠BOC =α, ∠BOA = β, ∠AOD = 180∘ − α, ∠DOC = 180∘− β

Сумма площадей треугольников $BCO$ и $ABO$ равна:

SBCO +SABO = 1R⋅R sinα+ 1R ⋅Rsinβ = 2 2

= 1R2(sinα+ sinβ), 2

где $R$ - радиус описанной окружности.

Сумма площадей треугольников $ADO$ и $CDO$ равна:

1 2 SADO+ SCDO = 2R (sin(π − α)+ sin(π − β))=

1 2 = 2R (sinα +sin β)=SBCO + SABO.

Таким образом, площадь четырехугольника $ABCO$ равна половине площади четырехугольника $ABCD$ , равной $12d1⋅d2 = 12 ⋅5⋅6 =15.$

Ответ: 7,5

Ошибка.
Попробуйте повторить позже

Задача 6#76942

Математический бильярд имеет форму параллелограмма $ABCD$ . На сторонах $AD$ и $CD$ соответственной расположены точки $E$ и $F$ так, что $AE :ED =1 :2$ , а $DF :FC =1 :3$ . Шар находится в точке $M$ пересечения прямых $BF$ и $CE$ . Известно, что шар, направленный в точку $N$ борта $BC$ , отразившись от четырех различных бортов, вернулся в точку $M$ и, продолжив свое движение, повторил свою предыдущую траекторию. Найти величину отношения $BN$ : $NC$ , если известно, что траектория шара — выпуклый четырехугольник.

Показать ответ и решение

Рассмотрим траекторию движения, следуя правилу "угол падения равен углу отражения". Пусть эти углы равны $α ,α ,α ,α 1 2 3 4$ для случаев отражения от бортов $BC$ , $AB$ , $AD$ , $CD$ соответственно. Тогда выполняются равенства $α1+ α4 = α2+α3$ и $α1+ α2 = α3+ α4$ из тех соображений, что противоположные углы параллелограмма равны. Из этих равенств вытекает, что $α1 = α3$ и $α2 = α4$ , из чего, в свою очередь, следует, что $ABCD$ – прямоугольник.

$PIC$

Введём аффинную систему координат, в которой $A(0;0)$ , $D(1;0)$ , $B(0;1)$ , $C(1;1)$ и выпишем уравнения прямых $CE$ и $BF$ . Поскольку $E(13;0)$ и $F(1;14)$ , прямые $CE$ и $BF$ задаются уравнениями:

y = 3x− 1 и y = − 3x+1 2 2 4

соответственно, а их точкой пересечения будет $M (2;1). 3 2$

Теперь отразим прямоугольник $ABCD$ зеркально сначала от стороны $BC$ , затем от стороны, в которую перешла $BC$ при этом отражении, и далее для двух оставшихся сторон по тому же принципу. Это стандартная процедура "выпрямления"бильярдной траектории, соответствующая равенству угла падения углу отражения.

$PIC$

При таких "зеркальных"отражениях траектория становится отрезком $MM ′$ , где $M ′$ - образ точки $M$ после серии отражений. Её координаты легко вычислить: после четырёх отражений прямоугольник сохранил ориентацию, и сдвинулся на два размера влево и на два размера вверх. Таким образом, $M ′(23 − 2;12 + 2)$ , и прямая $MM ′$ имеет угловой коэффициент $− 1$ . Её уравнением будет

y =− x+ 7 6

и прямую $BC$ , заданную уравнением $y = 1$ , она пересекает в точке с абсциссой $x= 16$ . Это значит, что точка $N$ , в которую был направлен шар, делит отрезок $BC$ в отношении $1:5$ .

Ответ: 1 : 5

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Предыдущий раздел

Следующий раздел