Тема Росатом

Стереометрия на Росатоме

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела росатом

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83301

Точка $O$ — начало трех отрезков $OA,OB$ и $OC$ лежащих в плоскости $P$ и имеющих длины 3,4 и 7 соответственно. На прямой $L$ , проходящей через точку $O$ и перпендикулярной плоскости $P$ , расположена точка $D$ так, что сумма углов, образуемых прямыми $DA, DB$ и $DC$ с прямой $L$ , равна $∘ 180$ . Найти длину отрезка $OD$ .

Источники: Росатом-2024, московский вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Треугольники ODA, ODB и ODC прямоугольные, также они имеют общую сторону OD. Если её обозначить за переменную, как можно будет записать условие на сумму трёх углов?

Подсказка 2

Пусть OD = x, тогда углы выражаются через арктангенсы. Тогда из условия получаем, что сумма трёх арктангенсов равна π. Что же хочется сделать? Взять от обеих частей тангенс! Но для тангенса суммы двух углов мы формулу знаем, чего не скажешь о суммы трёх. А вот π одиноко стоит с правой стороны, тогда можно сначала перенести одно слагаемое на правую часть и потом уже делать махинации со взятием тангенса.

Подсказка 3

Тогда взяв тангенс от обеих частей (но помните, что нужно будет сделать проверку равносильности такого перехода!) и применив формулу тангенса суммы, получаем совсем простое квадратное уравнение для x.

Показать ответ и решение

Обозначим $OD$ через $x$ .

$PIC$

Из прямоугольных треугольников выражаем углы

∠CDO =arctg 7 ,∠BDO =arctg 4,∠ADO = arctg 3 x x x

По условию нам дано

arctg 7 +arctg 4 + arctg 3= π x x x

Преобразуем

7 4 3 arctgx +arctgx = π− arctg x

Возьмём тангенс от обеих частей (проверку равносильности такого перехода отложим) и применим формулу тангенса суммы

tg(arctg 7x)+ tg(arctg 4x) 3 1−-tg(arctg 7)⋅tg(arctg 4) = tg(π − arctgx) x x

-11x--= − 3 1− 28x2 x

28 11 1− x2 =− 3-

x2 = 28⋅3= 6 14

$x= OD >0,$ поэтому подходит только $x= √6$ .

Теперь вернёмся к уравнению до взятия тангенсов и подставим туда этот корень. Правая часть $∘ -- π− arctg 32$ лежит на отрезке $(0,π).$ Левая тоже, потому что оба арктангенса по определению положительные и меньше $π2.$ То есть они не могут отличаться на кратное $π.$ Так что раз тангенсы получились равны, то и сами углы равны.

Ответ:

$√6$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#83311

Медианы оснований треугольной призмы $ABCA B C 1 1 1$ пересекаются в точках $O$ и $O 1$ соответственно. На отрезке $OO 1$ взята точка $P$ так, что $O1P :PO = 3:5$ . Через точку $P$ проведена прямая параллельная диагонали $A1C$ боковой грани призмы. Найти длину отрезка этой прямой, расположенного внутри призмы, если длина диагонали $A1C$ равна 2.

Источники: Росатом - 2024, региональный вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

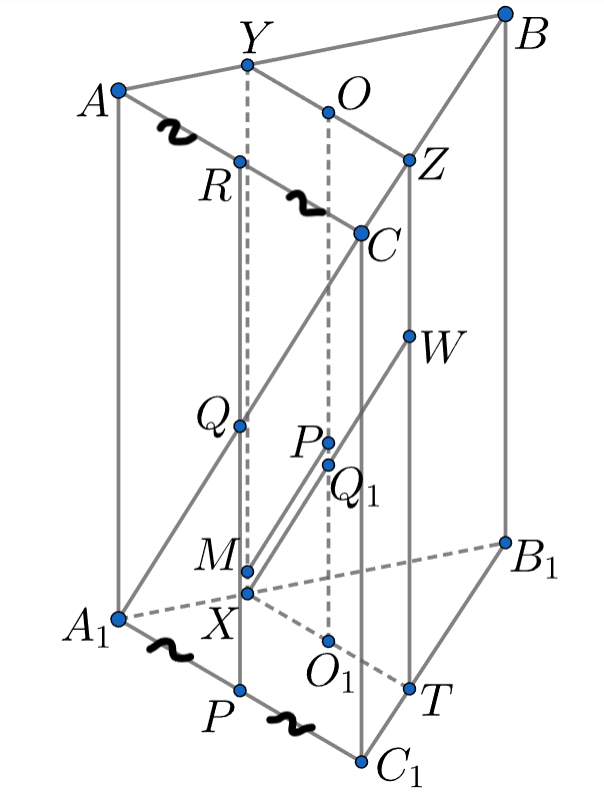
Рассмотрим сечение призмы XYZT, проходящее через OO₁ и параллельное грани ACC₁A₁. Прямая, проходящая через точку Р и параллельная А₁С, будет лежать как раз в этом сечении. А искомый отрезок - это часть этой прямой, ограниченная четырехугольником XYZT. А какой фигурой является XYZT? Как относятся ее стороны к сторонам призмы?

Подсказка 2

Верно, XYZT - параллелограмм. ZT = XY = A₁A, XT = YZ = 2/3 * AC, так как точка пересечения медиан делит медианы в отношении 2 к 1. Теперь нужно подумать, с помощью чего мы можем "перенести" плоскость ACC₁A₁ на плоскость XYZT?

Подсказка 3

С помощью гомотетии! Сделаем гомотетию в точке В₁ с коэффициентом 2/3. Подумайте, куда перейдут точки, лежащие в плоскости ACC₁A₁.

Подсказка 4

Например, точка А₁ перейдет в точку Х. Постройте прямые, параллельные А1С, через точки Х и Z. Чему будут равны отрезки этих прямых, отграниченные параллелограммом XYZT? Равна ли искомая прямая этим отрезкам?

Показать ответ и решение

Рассмотрим сечение призмы $XY ZT$ , проходящее через $OO 1$ и параллельное грани $ACC A 1 1$ . Это параллелограмм, а $OO 1$ — его средняя линия.

Сделаем гомотетию в точке $B1$ с коэффициентом $2 3$ . Тогда точки $A1$ и $C1$ перейдут в $X$ и $T$ , потому что точка пересечения медиан делит медиану в отношении $2$ к $1$ . Точка $Q$ перейдёт в точку $Q1$ , делящую отрезок $OO1$ в отношении $2$ к $1$ (до гомотетии отрезок $P Q$ был половиной $PR$ , а после он перешёл в $XQ1$ , который равен $1 3PR$ ). При этом прямая $XQ1$ будет пересекать отрезок $TZ$ в точке $W$ , поскольку в параллелограмме $ACC1A1$ прямая $A1C$ пересекает вершину $C$ , а в параллелограмм $XYZT$ отличается от $ACC1A1$ лишь тем, что длины сторон $YZ$ и $XT$ короче, а значит, точка пересечения прямой $XQ1$ с прямой $TZ$ будет лежать ниже точки $Z$ .

$PIC$

Аналогично, прямая, проходящая через $Z$ параллельно прямой $A1C$ будет делить $OO1$ в отношении $2$ к $1$ , но уже считая от точки $O$ , и она будет проходить через отрезок $XY$ . Значит, прямая $MP$ будет лежать между этими двумя прямыми и также проходить через отрезок $TZ$ . Значит, отрезок нужной прямой — это отрезок прямой $MP$ , содержащийся в параллелограмме $XY ZT$ .

Поскольку $MP ∥ XW$ , длина этого отрезка будет равна $XW$ . Отрезок $XQ1$ — образ $AQ$ при гомотетии, значит, он равен $23AQ = 23$ .

Также $XQ1 = Q1W$ , то есть искомая длина — $43$ .

Ответ:

$4 3$

Ошибка.
Попробуйте повторить позже

Задача 3#68079

На ребре $AC$ основания треугольной пирамиды $ABCD$ расположена точка $M$ так, что $AM :MC = 1:2$ . Через середину ребра $BC$ основания пирамиды проведена плоскость $P$ , проходящая через точку $M$ и параллельная боковому ребру $CD$ . В каком отношении плоскость $P$ делит объем пирамиды?

Источники: Росатом-2023, 11.6, Москва (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала построим сечение плоскостью P нашей пирамиды.

Подсказка 2

Пользуясь параллельностью, мы сможем из подобия найти, в каком отношении плоскость P делит рёбра пирамиды, а значит мы сможем найти и...

Подсказка 3

Как относятся высоты маленьких пирамидок и высотам из точек A и D пирамиды ABCD.

Подсказка 4

Нам достаточно найти, какую часть объёма всей пирамиды ABCD составляет объём многогранника, лежащего со стороны вершины A. Чтобы найти его объём, можно...

Подсказка 5

Разбить его на две пирамидки. А объём каждой из них мы сможем выразить через объём всей пирамиды ABCD, потому что знаем отношения высот и отношения площадей оснований.

Показать ответ и решение

Построим сечение. Поскольку секущая плоскость параллельна ребру $CD$ , она пересечет плоскость $ACD$ по прямой $MP$ , параллельной $CD$ , а плоскость $BCD$ — по прямой $NQ$ , также параллельной $CD$ . Соединим точки $P$ и $Q$ , лежащие в одной плоскости, и точки $M$ и $N$ , лежащие в одной плоскости, получим $MP QN$ — искомое сечение.

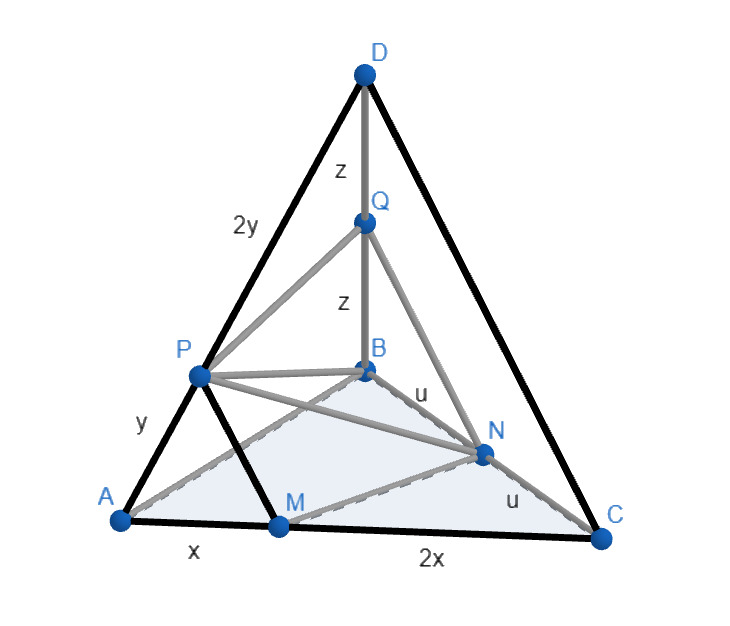
Пусть $V$ — объем пирамиды, $V1$ — сумма объемов пирамид $PABNM$ и $PQBN$ и $V2 = V − V1$ .

Из подобия пар треугольников $ACD$ и $AMP$ и из условия задачи получим, что

AM = x,MC = 2x,AP = y,P D =2y

Отсюда следует, что

y- 1 HP = 3y ⋅HD = 3HD,

где $HP$ — высота, опущенная из вершины $P$ пирамиды $PABNM$ , $HD$ — высота, опушенная из вершины $D$ пирамиды $ABCD$ .

А также значит, что площадь основания пирамиды $P ABNM$ равна:

2x u 2 SABNM =SABC − SMNC = SABC − 3x ⋅ 2u-⋅SABC = 3SABC

Тем самым:

VPABNM = 1HP ⋅SABNM = 1 ⋅ 1⋅HD ⋅ 2SABC = 2V 3 3 3 3 9

Аналогично из подобия пар треугольников $BCD$ и $BNQ$ и из условия задачи получим, что

CN =NB =u,BQ = QD = z

Отсюда следует, что

′ 2y 2 HP = 3y ⋅HA = 3HA,

где $H ′P$ — высота, опущенная из вершины $P$ пирамиды $PQBN$ , $HA$ — высота, опущенная из вершины $A$ пирамиды $ABCD$ .

А также значит, что площадь основания пирамиды $P QBN$ равна:

SBNQ = u-⋅ z-⋅SBCD = 1SBCD 2u 2z 4

Тем самым:

1 ′ 1 2 1 1 VPQBN = 3HP ⋅SQBN =3 ⋅3HA ⋅4SDBC = 6V

Теперь можно записать, что

2 1 7- V1 = VPABNM + VPQBN = 9V + 6V = 18V

7 V1= --V1--= --18V--= -7 V2 V − V1 V − 7V 11 18

Ответ:

$-7 11$

Ошибка.
Попробуйте повторить позже

Задача 4#48862

По диагоналям оснований $AC$ и $B D 1 1$ куба $ABCDA B C D 1 1 1 1$ с ребром $a$ ползут два муравья Гоша и Леша. Движение они начали одновременно из точек $A$ и $B1$ соответственно с постоянной скоростью, причем скорость Леши была в два раза больше скорости передвижения Гоши и закончили, когда Леша оказался в точке $D1$ . Какое наименьшее расстояние разделяло Гошу и Лешу во время движения?

Источники: Росатом-2022, московский вариант, 11.6 (см. olymp.mephi.ru)

Показать ответ и решение

$PIC$

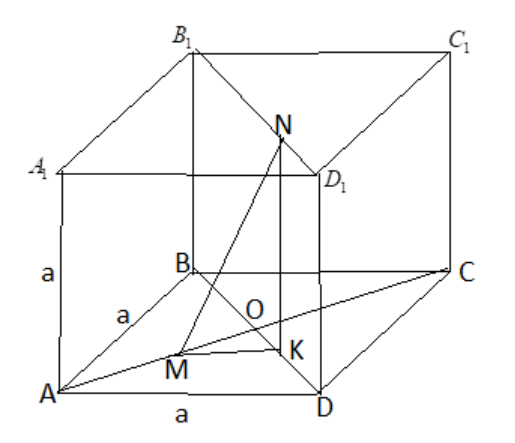
Фиксируем момент времени $t$

$M, N$ — положение муравьёв в момент $t$ .
$K$ — проекция точки $N$ на диагональ $BD$ .
$ν$ — скорость движения Гоши, $2ν$ — скорость Леши.

Тогда имеем

B1N = BK = 2νt

2 2 ( a )2 ( a )2 AM = νt,KD = 2νt =⇒ OM + OK = √2 − νt + √2-− 2νt

Наконец,

( )2 ( )2 MN2 = f(t)= MK2 + NK2 =a2+ a√-− νt + a√-− 2νt 2 2

Движение закончилось, когда последняя скобка занулилась, то есть при $t= √a2ν$ . Относительно $t$ функция $f(t)$ является квадратным трёхчленом с положительным коэффициентом при $t2$ . Вершина находится в точке $t= t = -a√-⋅ 3 ≤-a√- верш μ 2 5 μ 2$ . Отсюда $2( ) 2 ∘-- fmin = f(tверш)= a2 3− 45 = a1110 =⇒ dmin = a 1110-$ .

Ответ:

$a∘ 11 10$

Ошибка.
Попробуйте повторить позже

Задача 5#76648

Точка $M$ лежит на ребре $AB$ куба $ABCDA B C D . 1 1 1 1$ В квадрат $ABCD$ вписан прямоугольник $MNLK$ так, что одной из его вершин является точка $M,$ а три другие расположены на различных сторонах квадрата основания. Прямоугольник $M1N1L1K1$ является ортогональной проекцией прямоугольника $MNLK$ на плоскость верхнего основания $A1B1C1D1.$ Диагонали четырехугольника $MK1L1N$ перпендикулярны. Найти отношение $AM :MB.$

Источники: Росатом-2022, московский вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте ещё рассмотрим четырёхугольник MK₁L₁N. Что мы можем сказать о параллельности его сторон, углах; в целом, какого рода этот четырёхугольник?

Подсказка 2

Так как его стороны MN и L₁K₁ равны и параллельны, то MK₁L₁N — параллелограмм. Также рассмотрим его углы, воспользовавшись теоремой о трёх перпендикулярах. И о чём в таком случае говорит перпендикулярность диагоналей?..

Подсказка 3

Правильно, MK₁L₁N — квадрат. Обозначим сторону куба за а. Тогда можно выразить из AB отрезки AM и MB (пусть один из отрезков равен λa, где λ - некоторая неизвестная). Теперь, чтобы найти отношение АМ:МВ, нам достаточно просто найти λ.

Подсказка 4

MK₁ и MN равны как стороны квадрата MK₁L₁N и к тому же легко выражаются через длины АМ и МВ с помощью нескольких теорем Пифагора. Осталось только верно выразить эти стороны через λ и а и приравнять, сократив а. И не забудьте, что главный вопрос задачи — найти отношение, а не λ!

Показать ответ и решение

$K L ||KL ||MN 1 1$ и $K L = KL = MN 1 1$ , поэтому четырехугольник $MK L N 1 1$ — параллелограмм. По теореме о трёх перпендикулярах угол $∠K1MK$ прямой, поэтому $MK1L1N$ — прямоугольник. Его диагонали по условию перпендикулярны, поэтому $MK1L1N$ — квадрат.

Пусть $a$ — ребро куба, $AM = λa$ с неизвестным $λ ∈(0;1).$

$PIC$

Тогда $MK = λa√2,MN = (1 − λ)a√2$ и по теореме Пифагора

K1M2 = MK2 + KK21 = 2λ2a2+ a2 = a2(2λ2+ 1)

Стороны $MK1$ и $MN$ равны, поэтому

2(1− λ)2a2 = a2(2λ2+1)

2λ2− 4λ+2 =2λ2+ 1

1 λ = 4

В итоге

a 3a AM = 4,MB = 4 ,

так что $AM :MB = 1:3.$

Ответ: 1 : 3

Ошибка.
Попробуйте повторить позже

Задача 6#76662

На ребре $AD$ основания $ABCD$ куба $ABCDA ′B′C′D′$ расположена точка $M$ так, что $AM :AD = 1:3$ . Через точку $M$ и вершины $′ A$ и $′ C$ куба проведена плоскость $P$ . Найти расстояние до плоскости $P$ точки $N$ , расположенной на ребре $AB$ так, что $AN :AB = 1:2$ , если длина ребра куба равна $√-- 2 19$ .

Источники: Росатом - 2021, 11.6, комплект 1 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте подумаем: у нас есть куб, плоскость, понятная точка и нам надо найти расстояние от этой точки до плоскости(которая задана тремя понятными точками). Нам это намекает явно на то, чтобы посчитать все в координатах с центром в точке А и параллельно сторонам квадрата.

Подсказка 2

Направим ось х вдоль AD, ось у вдоль AB, ось z вдоль AA’. Чтобы не возиться с корнями, обозначим ребро куба через a. Какие нам точки нужны для того, чтобы задать плоскость? Понятны ли нам координаты точки N?

Подсказка 3

Нам нужны точки A’, M, C’. Их координаты мы можем явно выразить через а. А значит, можем найти уравнение этой плоскости. А значит, можем по формуле расстояния от точки до плоскости, можем найти это расстояние, ведь нам все известно.

Показать ответ и решение

Введем декартову систему координат с началом координат в точке $A$ , ось $x$ направим вдоль $AD$ , ось $y$ – на плоскости основания $ABCD$ перпендикулярно оси абсцисс и ось $z$ перпендикулярно плоскости основания.

Обозначим ребро куба через $√ -- a =2 19$ , отношения $AM- 1 AD = 3$ , $AN- 1 AB = 2$ .

Выписываем координаты нужных нам точек: $′ A (0,0,a)$ , $a M (3,0,0)$ , $a N (0,2,0)$ , $′ C (a,a,a)$ .

Находим уравнение плоскости $P$ в виде $Ax+ By+ Cz+ D =0$ , подставив координаты точек $′ ′ M, A,C$ . При этом так как плоскость не проходит через начало координат, то без ограничения общности можно считать, что $D = 1$ .

Получим систему:

( a |{ A3 + 1 = 0 |( Ca+ 1 = 0 Aa+ Ba+ Ca+ 1 = 0

Откуда получаем, что

3 3 1 A = −a,B = a,C = −a

Находим расстояние $d$ от точки $N$ до плоскости $P$ по формуле

|Ax + By + Cz + D| d = --0√A2-+0B2+-0C2---

, где $(x0,y0,z0)$ - координаты точки $N$ .

Получим

|0+ 3a ⋅ a2 + 0+1| d = ---∘-9+9+1----= a2

-5-- --5- √-- = 2√19a= 2√19 ⋅2 19 =5

Ответ: 5

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#76663

Длины всех ребер (боковых и основания) тетраэдра $ABCD$ равны 1 . На ребре $AB$ расположена точка $M$ так, что $AM :AB =1 :3$ . Найти расстояние между скрещивающимися прямыми $CM$ и $AD$ .

Источники: Росатом - 2021, 11.6, комплект 2 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Мы видим, что нам надо найти расстояние между двумя скрещивающимися прямыми, при этом конструкция фигуры понятна и все отрезки известны. Что в таком случае мы привыкли делать?

Подсказка 2

Вводить систему координат с началом в точке A, ось х - вдоль AB, ось у - перпендикулярно оси х и в плоскости треугольника АВС. А ось z - просто перпендикулярно плоскости основания. Чтобы найти расстояние между скрещивающимися прямыми, можно найти расстояние между прямой и плоскостью, которая проходит через одну и параллельна другой прямой. Что нам нужно чтобы найти такую плоскость?

Подсказка 3

Верно, чтобы найти такую плоскость, нам нужны оба вектора AD и MC (ведь их векторное произведение - направляющий вектор нормали к плоскости, а вектор нормали к плоскости и коэффициенты канонического уравнения плоскости очень хорошо связаны). Как найти эти векторы? Через что их можно выразить?

Подсказка 4

Заметим, что вектор СМ понятным образом выражается через вектора BC и AB (ведь мы знаем в каком отношении точка M делит AB). А вектор AD понятно выражается через высоту тетраэдра из точки D на ABC, и отрезок AO (O - центр вписанной и описанной окружности треугольника ABC). А вектор AO выражается через CE и AB, где Е - середина AB. Значит, все понятно выражается и остается только это сделать и найти по формуле расстояние от точки прямой до плоскости и записать ответ!

Показать ответ и решение

Введем декартову систему координат с началом координат в точке $A$ , ось $x$ направим вдоль $AB$ , ось $y$ – на плоскости основания $ABC$ перпендикулярно оси абсцисс, а ось $z$ перпендикулярно плоскости основания тетраэдра.

$PIC$

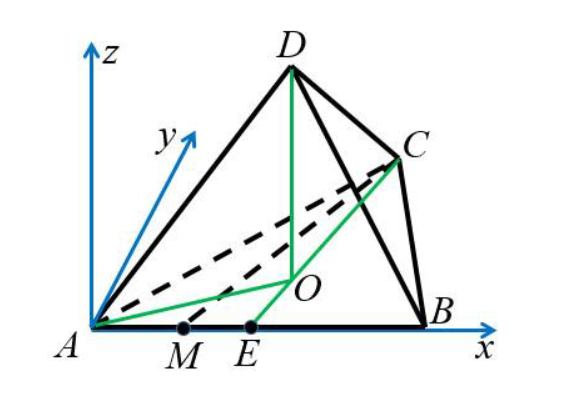
Из условия $1 1 AM = 3AB = 3$ . Пусть $E$ – середина $AB$ . Так как все ребра тетраэдра равны $1$ , то радиус окружности, описанной около равностороннего треугольника в основании: $√3 R= AO = 3$ .

Радиус окружности, вписанной в основание: $√3 r= EO = 6$ .

Из прямоугольного треугольника $DAO$ находим высоту пирамиды:

∘ --------- ∘----- √- DO = AD2 − AO2 = 1 − 13 =-63-

Высота равностороннего треугольника $ABC$ со стороной $1$ : $√ - CE = -23$ .

Теперь можно выписать координаты всех нужных точек: $A(0,0,0)$ , $√- √- D (12,63,36)$ , $M (13,0,0)$ , $√- C(12,23,0)$ .

Таким образом

√ - √- √- −−→AD ={1,--3,-6};−−M→C = {1,-3,0} 2 6 3 6 2

Напишем уравнение плоскости, проходящей через ребро $AD$ параллельно $CM$ . Найдем вектор, перпендикулярный этой плоскости

√- √ - √- √ - √ - √- −→N =−A−→D × −M−→C = {1,-3,--6}× {1,-3,0} = 1-⋅({3,√3,2√6-}×{1,√3,0})= 1{− 6√2,2--6,8-3}= -6{−3√3,1,2√2-} 2 6 3 6 2 12 3 12 3 3 18

Уравнение искомой плоскости:

√ - √- −3 3x +y+ 2 2z = 0

Искомая в задаче величина равна расстоянию $d$ от точки $M$ до этой плоскости:

|−-3√313 +-0+-0| √3- d= √27-+1+-8- = 6

Ответ:

$√3 6$

Ошибка.
Попробуйте повторить позже

Задача 8#76664

Боковое ребро правильной треугольной пирамиды наклонено к плоскости ее основания под углом $45∘$ . В пирамиду вписан куб так, что четыре его вершины лежат на основании пирамиды, а другие четыре — на ее боковых гранях. Найти отношение объемов куба и пирамиды.

Источники: Росатом - 2021, 11.6, комплект 3 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте для начала обозначим за a ребро пирамиды. Получается нам нужно выразить объёмы фигур через a. Начнём с пирамиды. Для объёма нам нужны основание и высота. Так как пирамида у нас правильная, то куда падает её высота?

Подсказка 2

Верно, в центр основания правильного треугольника, то есть в центр описанной окружности. Теперь радиус мы можем легко найти, а угол будет как раз тот самый из условия. Отлично, высота найдена. А площадь основания равна площади правильного треугольника. Давайте теперь попробуем разобраться с кубом. Удобно будет ввести ребро куба b и попробовать выразить его через a. Тогда будет победа. Но какую ещё вспомогательную фигуру хочется рассмотреть, учитывая расположение куба?

Подсказка 3

Да, давайте рассмотрим сечение, которое получается из-за куба. Понятно, что это будет треугольник, подобный основанию, и мы даже знаем коэффициент подобия треугольников. То есть мы знаем длину стороны сечения. Как теперь можно вторым способом посчитать это основание?

Подсказка 4

Верно, рассмотрим сечение как треугольник, внутрь которого вписан квадрат. Мы легко можем выразить, как сумму отрезков, сторону треугольника через b. Наконец с помощью равенства из прошлой подсказки выражаем b через a и находим объём куба. Осталось только посчитать отношение, и победа!

Показать ответ и решение

Пусть $a$ – сторона основания, $α= 45∘$ – угол наклона бокового ребра, $H$ – высота пирамиды, $R = AO$ — радиус окружности, описанной около основания. В правильном треугольнике со стороной $a$ радиус описанной окружности: $a√- R= AO = 3$ .

Из прямоугольного треугольника $SAO$ находим высоту пирамиды: $a√- H = AO ⋅tgα = 3$ .

$PIC$

Площадь основания пирамиды

√ - S = 1a⋅a⋅sin(60∘)= a2-3 2 4

Объем пирамиды:

1 1 a2√3 a a3 V1 = 3S⋅H = 3 ⋅-4 ⋅√3-=12

Пусть $b$ ребро вписанного куба и $A1B1C1$ – сечение пирамиды плоскостью верхней грани куба.

$PIC$

Обозначим через $a1$ сторону треугольника этого сечения $a1 =A1B1$ . Треугольники $ABC$ и $A1B1C1$ подобны с коэффициентом подобия: $k = H−b= a−b√3 H a$ .