Алгебраические текстовые задачи на Росатоме
Ошибка.
Попробуйте повторить позже
Компания друзей совершала пробежку по прямолинейному участку шоссе: мальчики бежали в одном направлении, девочки — в
противоположном. Через мин после того, как Паша обогнал Ваню, он поравнялся с Таней, а затем через
мин оказался рядом с
бегущей Машей. Спустя еще
мин Маша повстречалась с Ваней. Наконец, еще
мин понадобилось ей чтобы догнать Таню. Известно,
что
а
Сколько времени было на часах, когда Ваня поравнялся с Таней, если известно, что Паша догнал Ваню
в 12 часов дня, Маша была в одной точке шоссе с Ваней в момент, когда часы показывали 14 часов, а скорость бега всех участников была
постоянной и различной для каждого?
Источники:
Подсказка 1
Заметим, что в условии даны отношения отрезков, конкретное время встреч, так еще и сказано про разные скорости движения. Как удобнее всего интерпретировать это?
Подсказка 2
Да! Давайте изобразим все на координатной плоскости с осями времени и пути. Тогда встречи – пересечения отрезков. Введём все необходимые нам обозначения и все те, которые даны нам в условии (пусть t — время встречи Вани и Тани). Что из условия теперь можно использовать?
Подсказка 3
Конечно! Давайте запишем данные в условии отношения. Сперва используем t₁ : t₂ , затем t₃ : t₄. Не забудем, что отношение отрезков равно отношению их проекций на оси. Какую теорему теперь хочется применить?
Подсказка 4
Верно! Применим теорему Менелая. Найдем последнее отношение отрезков. Зная его, можно найти и отношение их проекций, выраженных через t!
Изобразим на координатной плоскости графики зависимости координаты от времени для участников пробежки
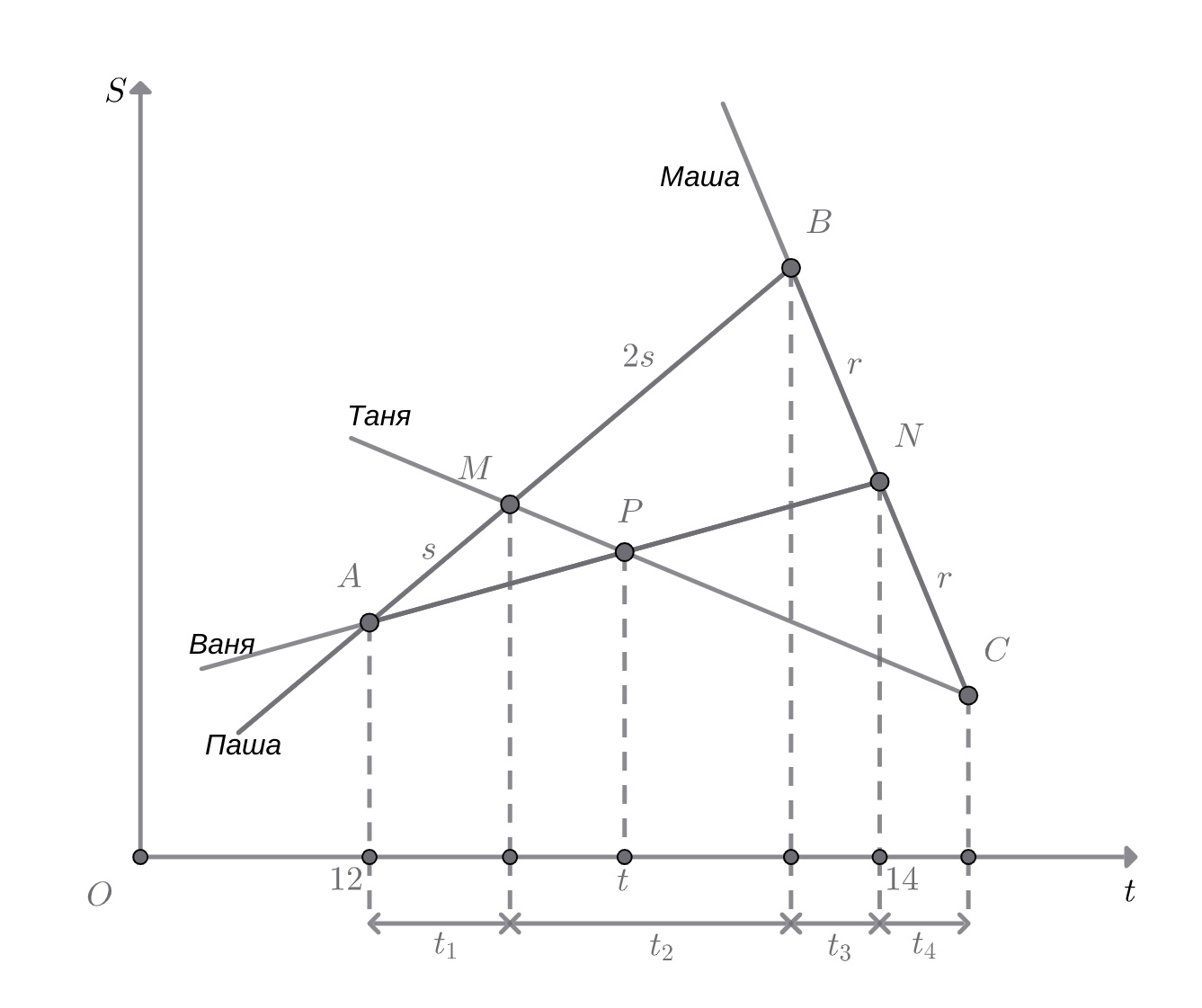
Вершины треугольника — точки встречи Вани и Паши
Маши и Паши
Маши и Тани
Точка
на
стороне
треугольника — точка встречи Паши и Тани. Точка
на стороне
треугольника — точка встречи
Вани и Маши.Точка
— пересечение отрезков
и
— точка встречи Вани и Тани,
— время встречи Вани и
Тани.
Так как то пусть
и
— длины отрезков
и
соответственно; аналогично, так как
то пусть
и
— длины отрезков
и
соответственно.
По теореме Менелая для имеем:
Так как отношение отрезков такое же, как отношение их проекций, то
Получаем
13
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




