Алгебраические текстовые задачи на Росатоме
Ошибка.
Попробуйте повторить позже
Петя и Вася пригласили одноклассников на свой день рожденья в дом Пети и посадили всех за круглый стол пить чай. Петя отметил для себя наименьшее число стульев, разделяющих его с каждым из приглашенных гостей, кроме Васи. Сложив полученные числа, он получил 60 . Найти число стульев за столом, если известно, что оно четное. Какое наименьшее число стульев разделяло Петю и Васю?
Источники:
Подсказка 1
Давайте попробуем для начала ввести удобные обозначения для количества людей между Петей и человеком. Заметим, что Петя считал наименьшие расстояния до людей на окружности. Тогда что особенного с подсчётом на ней? Можем ли мы просто пронумеровать подряд людей, и это будет правильно?
Подсказка 2
Верно, когда мы считаем наименьшее число на окружности, например, по часовой стрелке, то при переходе через середину это число уже не будет наименьшим, потому что мы могли пойти против часовой и получить меньшее число. Значит, мы нумеруем людей через подсчитанные расстояния Пети до середины, а потом в обратном порядке. Учитывая, что всего чётное число людей, найти сумму этих расстояний, включая Васю не составляет труда. Чтобы воспользоваться дальнейшим условием задачи, что хорошо ввести?
Подсказка 3
Да, можно ввести то, что спрашивают у нас в задаче. То есть пусть всего людей было 2n, а подсчитанное расстояние до Васи это y. Тогда мы понимаем как записывается то, что посчитал Петя и чему оно равно по условию. Также можно написать условие для расстояния до Васи, снова учитывая, что мы считаем его на окружности. У нас получилась система, решив которую для натурального n, мы получим ответы на задачу.
Пусть за столом стояло стульев (т.е. за столом сидело всего
человек). На круге точками отмечены стулья. Числом рядом с точкой
обозначено количество стульев, разделяющих Петю и человека, сидящего на этом стуле.
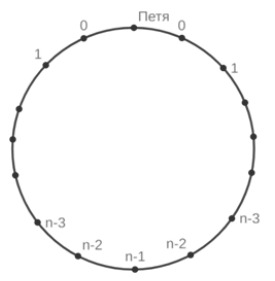
Тогда число стульев, посчитанных Петей, включая Васю, равно
Обозначим число стульев, вычисленное для Васи. Тогда
|
|
Учитывая, что ,
,
, получим единственное натуральное решение двойного неравенства:
.
Тогда число стульев за столом равно
, а количество стульев, разделяющих Петю и Васю,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




