Алгебраические текстовые задачи на Росатоме
Ошибка.
Попробуйте повторить позже
На проволоку в форме окружности радиуса 6 нанизаны 5 одинаковых бусинок, равноотстоящих друг от друга. В некоторый момент
времени 4 бусинки начали двигаться со скоростью сек) в направлении против часовой стрелки, а оставшаяся бусинка с
той же скоростью в обратном направлении. После столкновения любых двух бусинок величина скорости их движения
сохраняется, а направление мгновенно меняется на противоположное. Сколько столкновений произойдет между бусинками за 48
секунд?
Для начала решим задачу в общем виде. Пусть (бусин всего) ,
сек),
и
(сек). Рассмотрим столкновение
двух бусинок
и
.
До столкновения бусинки двигались навстречу друг другу. После столкновения — наоборот, удаляются друг от друга.
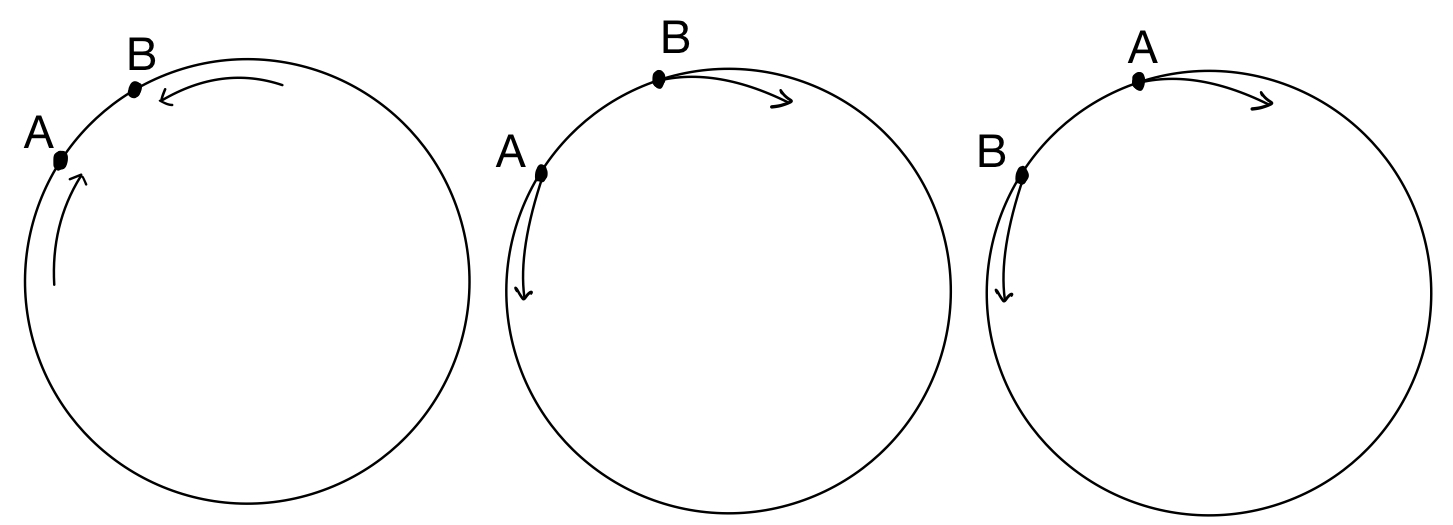
Так как бусинки по виду одинаковые, то поменяв на правом рисунке буквы и
местами, можно интерпретировать столкновение как
переход бусинки
через бусинку
(так как бусинка
теперь движется так, будто продолжает движение бусинки
). За один оборот
окружности по часовой стрелке образ бусинки
совершает
столкновение. С учётом относительности движения один оборот
совершается за
сек. Если число
ему кратно, то за время
совершается
полных оборотов, что сопровождается
столкновениями. Итого:
Возвращаясь к замене переменной, получаем ответ:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




