Планиметрия на ФЕ
Ошибка.
Попробуйте повторить позже
Дан треугольник Точки
— середины сторон
соответственно, а
— точки, в которых эти
стороны касаются вписанной окружности. Пусть отрезок
имеет с окружностью, вписанной в
общих точек;
с
окружностью, вписанной в
—
общих точек;
с окружностью, вписанной в
—
общих точек. Найдите
максимальное значение числа
Источники:
Подсказка 1
Чему равняется a+b+c в равностороннем треугольнике?
Подсказка 2
В равностороннем треугольнике a+b+c = 3. А если треугольник ABC — не равносторонний? Скажем, что меньшая сторона в нем — AC, AC = y, BC = x, AB = z. Как можно попробовать воспользоваться точками, данными в условии?
Подсказка 3
А если сделать гомотетию в B с коэффициентом 2 (растянуть треугольник A₁BC₁ до треугольника ABC)?
Подсказка 4
Пусть точка A₂ перейдет в A₃, точка С₂ — в С₃, что можно сказать о величинах отрезков BA₃ и BC₃?
Подсказка 5
Их можно вычислить, например, поняв, что BA₂ = (x + z - y)/2. Также на картинке присутствуют отрезки касательных к окружности, проведенные из одной точки.
Подсказка 6
Как можно оценить BA₃ и BC₃, если y меньше x и z?
Подсказка 7
Получим, что BA₃ ≥ x и BC₃ ≥ z, причём одно из неравенств строгое (иначе треугольник окажется равносторонним). Какие выводы можно сделать из этих оценок?
Подсказка 8
Будет ли A₃C₃ пересекать вписанную окружность?
Заметим, что в равностороннем треугольнике Пусть треугольник не равносторонний, его меньшая сторона —
Сделаем гомотетию в
с коэффициентом
(растянем треугольник
до треугольника
тогда
вписанная окружность треугольника
перейдет во вписанную окружность треугольника
Пусть
переходит в
— в
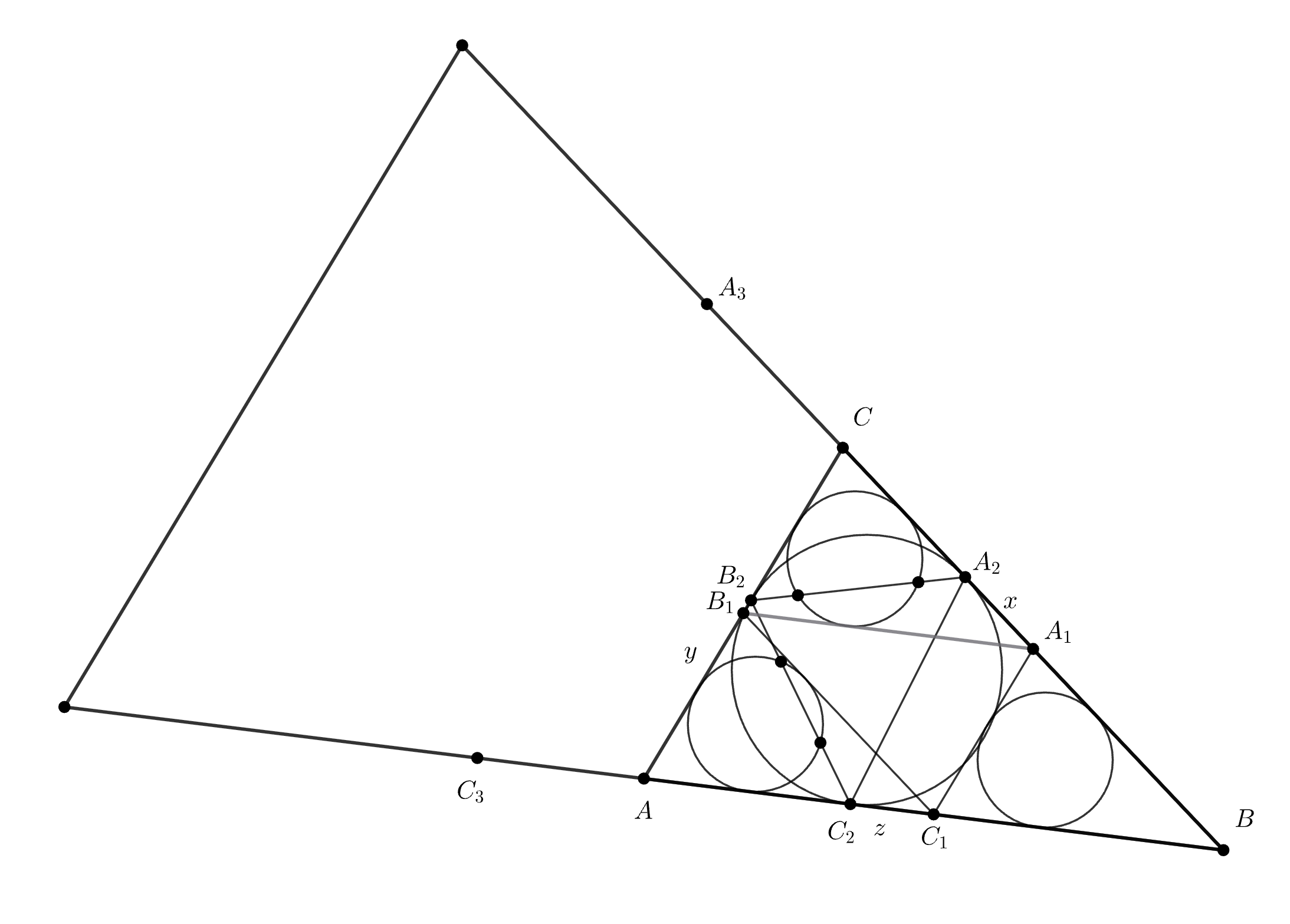
Тогда
Значит,
Так как то
и
причём одно из неравенств строгое (иначе треугольник окажется
равносторонним). Значит,
не пересекает вписанную окружность, поэтому
и
В качестве примера
можно взять треугольник с длинами сторон
Для него
отрезки
и
исходят из вершины
треугольников
и
причем их вторые концы лежат строго внутри противолежащих сторон, так как
4
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




