Задачи с неравенствами
Ошибка.
Попробуйте повторить позже
На заводе имеются в достаточном количестве три сплава титана, алюминия и молибдена. Все сплавы с примесями. Процентное содержание компонентов в этих сплавах приведено в таблице.
| 1 | 2 | 3 | |
| Молибден | | | |
| Титан | | | |
| Алюминий | | | |
Из этих сплавов необходимо приготовить новый сплав, в котором алюминия должно быть не больше , а молибдена - не меньше
.
Какое наибольшее и какое наименьшее содержание титана (в процентах) может быть в этом сплаве?
Источники:
Подсказка 1
Давайте сначала просто посчитаем. Пусть мы взяли x,y и 1-x-y первого, второго и третьего сплавов соответственно. Тогда как выглядят наши условия на нужный сплав и что мы хотим максимизировать/минимизировать?
Подсказка 2
Вы получили условия в виде неравенства для x и y, и выражение, которое надо максимизировать/минимизировать. Может быть, на плоскости эти неравенства будут нагляднее?)
Подсказка 3
Нам по факту надо найти макс/мин выражения 6+30x+15y. Понятно, что минимум будет в точке (0, 0). А чтобы найти максимум, можно заметить, что коэф при x больше, чем коэф при y....)
Первое решение.
Заметим, что как бы ни изготавливали новый сплав, содержание титана в нём будет не меньше минимального из содержаний
титана в имеющихся сплавах. Поэтому содержание титана в любом изготовленном сплаве будет не менее . С другой
стороны, сплав 3 подходит под условия на содержание алюминия и молибдена. Значит, наименьшее содержание титана
.
Теперь найдём наибольшее содержание титана в таком сплаве. Заметим, что если при изготовлении нового сплава мы использовали сплав 2, то можно его заменить на сплав 1: от этого содержание алюминия уменьшится, а молибдена и титана - увеличится. Поэтому в сплаве с наибольшим содержанием титана не участвует сплав 2.
Сразу отметим, что тогда в таком сплаве будет молибдена, т.е. он подходит под условие на молибден. В сплаве 1 титана больше, чем
в сплаве 3 , но сплав 1 не подходит под условие на алюминий. Понятно, что чем меньше мы возьмём сплава 3, тем больше будет титана в
изготовленном сплаве. Возьмём ровно столько, чтобы выполнилось условие на алюминий:
и
масса сплава 1 и 3
соответственно), откуда
, т.е. можно взять 23 части сплава 1 и 17 частей сплава 3. Тогда содержание титана в процентах
будет
Второе решение.
Пусть взято и
первого, второго и третьего сплава соответственно, причём
. Тогда условия
задачи можно записать так:
Изобразим на координатной плоскости область (см. рисунок), удовлетворяющую системе неравенств
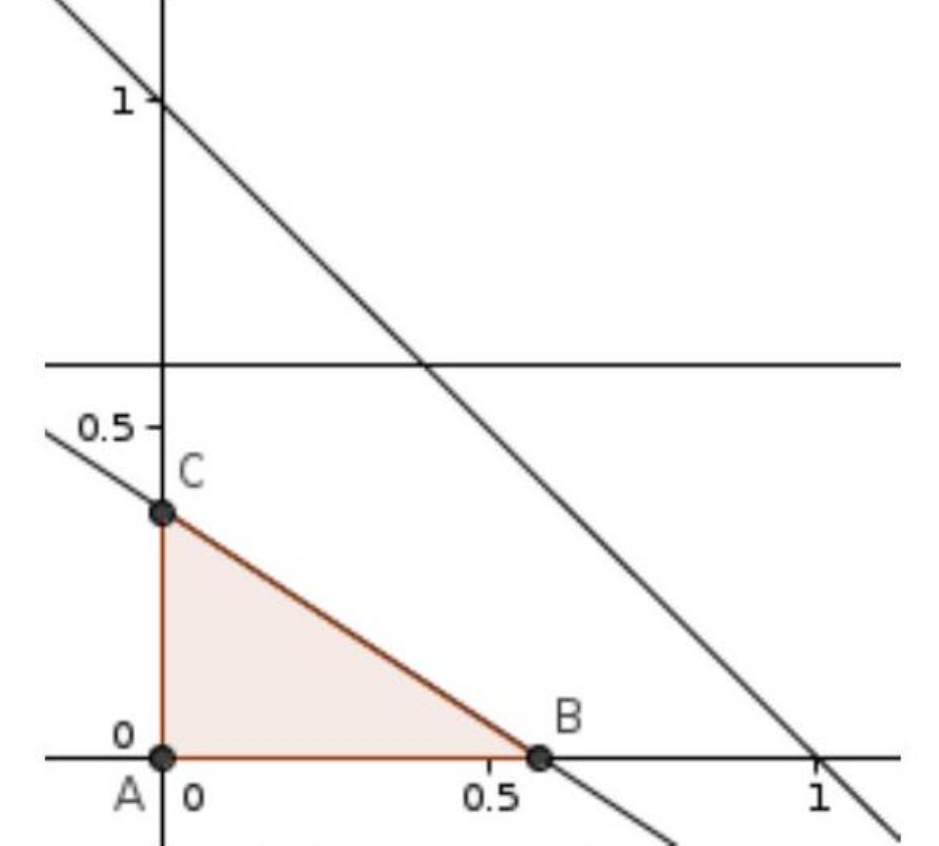
Процентное содержание титана . Легко видеть, что минимум этого числа достигается в точке
и равен 6 . Чтобы найти максимум, заметим, что абсцисса точки
равна
, а ордината точки
. При этом
коэффициент при
в
больше. Значит, значение в точке
точно больше (мы большее число умножаем на большее число), и равно
наименьшее
наибольшее
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




