Задачи на движение: алгебраический подход
Ошибка.
Попробуйте повторить позже
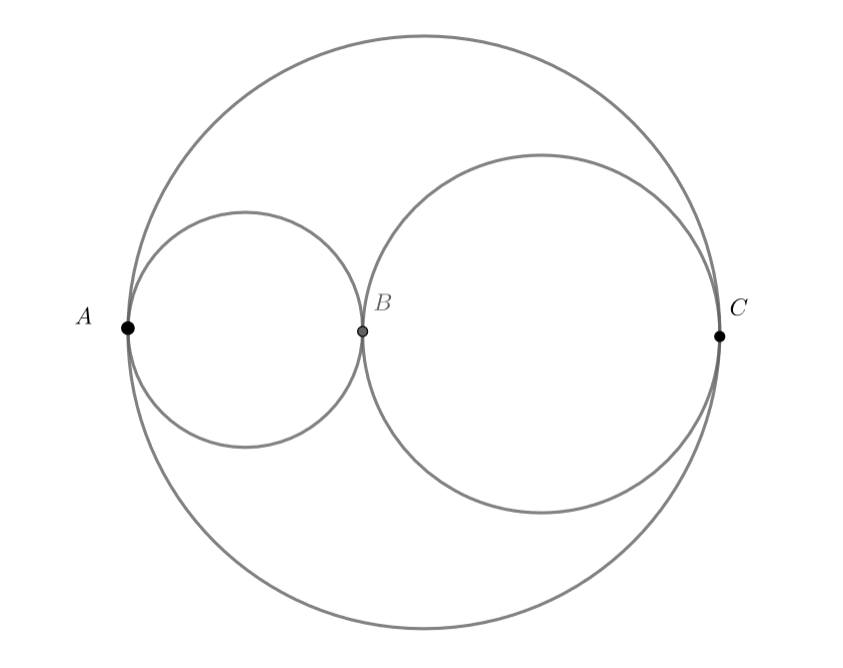
Автодром состоит из трех попарно касающихся кольцевых трасс (две окружности касаются друг друга попарно в точке внешним
образом и третьей в точках
и
внутренним, причём
— диаметр третьей окружности). Автомобиль в любой точке касания может
продолжать движение по любой из двух возможных трасс, но нигде не может разворачиваться на
. По каждой из трех трасс
автомобиль едет со своей скоростью, так что любую из двух
длиной
км он проезжает за
минут, любую из дуг
длиной
км — за
минут, а любую из дуг
— за
минут. Выехав из точки
, автомобиль через
час
минут оказался в ней же.
Сколько километров проехал автомобиль?
Источники:
Подсказка 1
Давайте сначала представим, как автомобиль будет ехать. Подумаем о четности. Сколько раз автомобиль может проехать по дугам AB, BC и AC?
Подсказка 2
Пусть автомобиль проехал по дуге AB i раз, по BC - j, по AC - k. Чтобы автомобиль приехал в ту же точку, с которой начал, нужно, чтобы i, j, k были все четные или все нечетные. Но что можно сказать про "четный" случай?
Подсказка 3
Этот случай не подходит, так как всего автомобиль проехал нечетное число минут. Осталось только решить уравнение в целых i, j, k.
Рассмотрим варианты, которыми находящийся в точке автомобиль может в следующий раз впервые снова оказаться в этой
точке.
Во-первых, можно сделать это, не проходя через точку , т. е. путем
.
Во-вторых, можно одним из двух способов ( или
) добраться до точки
, сделать несколько кругов
(«несколько»
может быть и нулем) и вернуться одним из двух способов (
или
) в точку
.
В любом случае мы либо четное число раз проезжаем по 7-минутной дуге, четное число раз по 11-минутной и четное число раз по 17 -минутной, либо наоборот, нечетное число раз по каждому из трех типов дуг.
То же самое можно сказать про неоднократное возвращение в точку .
«Четный» случай нам не подходит, так как по условию на каждую дугу уходит целое число минут, а общее время выражается в минутах
нечетным числом. Заметим, что любая тройка нечетных положительных чисел может быть реализована в качестве числа проходов (в любом
направлении) дуг ,
,
.
Действительно, выехав из точки и сделав заданное нечетное число проходов
, мы окажемся в точке
, после чего, сделав
заданное нечетное число проходов
, мы окажемся в точке
, а после заданного нечетного числа проходов
— снова в точке
.
Итак, попробуем найти три таких нечетных положительных числа ,
,
, что
Для возможны
варианта:
Первый случай отбрасываем, так как для него получаем
Во втором случае имеем . Если
, то
При
число
не делится на
.
Наконец, при имеем
. Для
получим
, откуда
а пройденный путь
равен
Здесь
— длина дуги
, которую находим геометрически:
где — радиусы.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




