Теорема косинусов и теорема Пифагора
Ошибка.
Попробуйте повторить позже
Внутри параллелограмма взята точка
так, что треугольник
равносторонний. Известно, что расстояния от точки
до
прямых
и
равны соответственно
и
Найти периметр параллелограмма.
Подсказка 1
Давайте обозначим за a угол MNP, а сторону равностороннего треугольника за x. Какие углы и отрезки можно посчитать через них?
Подсказка 2
Мы можем посчитать расстояния от точки P до KL и MN через x и угол a! Тогда у нас получится тригонометрическое уравнение, которое нужно решить.
Подсказка 3
6sin(60-a) = 10sin(a)! Чему равен a? Как выразить через него x?
Подсказка 4
Отлично, теперь мы знаем, чему равен x! Нам известны обе высоты параллелограмма. Какую характеристику у ABCD можно через них выразить?
Подсказка 5
Попробуем найти площадь ABCD двумя способами! Тогда мы сможем отыскать его стороны, а затем найти и периметр ;)
Пусть — расстояния от точки
до прямых
и
соответственно,
и сторона
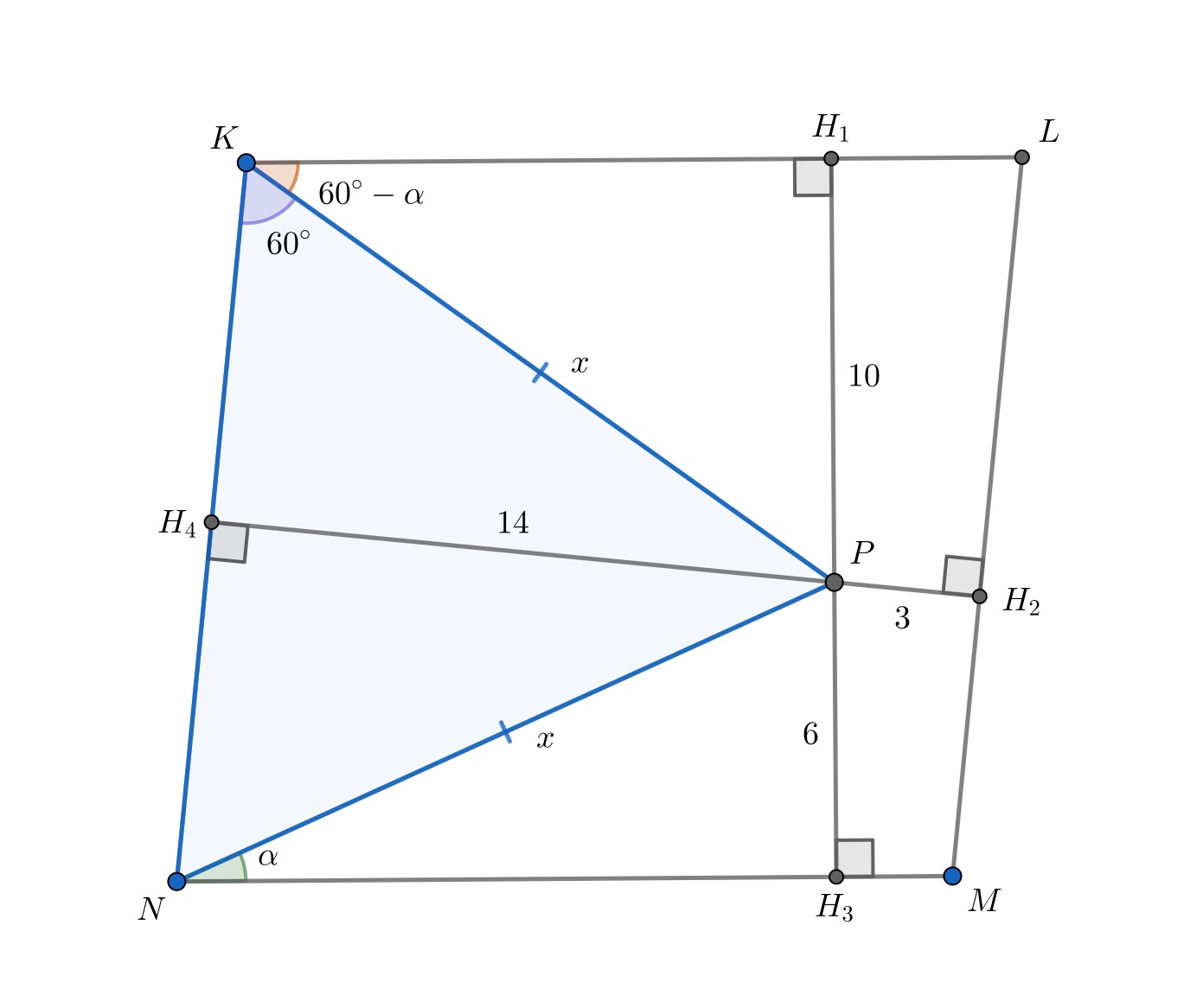
Тогда, так как — равносторонний, а
— параллелограмм, то
Из прямоугольных и
имеем:
То есть:
По формуле синуса разности:
Подставим в изначальное и получим:
Тогда выразим и
Можем теперь выразить
Тогда расстояние до из равностороннего
Тогда
Из того, что — параллелограмм, то по формуле площади:
Так как
Тогда можем посчитать периметр:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




