Теорема косинусов и теорема Пифагора
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Диагонали ромба пересекаются в точке
Прямая, проведённая из вершины
и перпендикулярная стороне
пересекает
эту сторону в точке
Известно, что
а) Докажите, что прямая касается описанной окружности треугольника
б) Найдите
![]()
а) Так как по условию
то по обратной теореме о касательной и секущей из
получаем, что — касательная к окружности описанной около
. Тогда
(угол между касательной и
хордой). При этом
Значит,
— касательная к окружности, описанной около
.
б) Пусть сторона ромба равна Рассмотрим
Теперь рассмотрим
По теореме
Пифагора в
По области значений косинуса подходит только
б)
Ошибка.
Попробуйте повторить позже
Высота треугольника
является диаметром окружности, которая пересекает стороны
и
в точках
и
соответственно. Прямые, касающиеся этой окружности в точках
и
пересекаются в точке
Прямая
пересекает сторону
в точке
Найдите отношение
:
и длины отрезков
и
если
Источники:
Подсказка 1
Что нам дает тот факт, что BH — диаметр окружности? Как это использовать при нахождении длин новых отрезков?
Подсказка 2
Все углы, опирающиеся на BH в нашей окружности — прямые! Тогда на картинке немало подобных треугольников, а также есть касательные, про которые мы также знаем полезные свойства для нахождения длины. Используя это, нам не составит труда найти стороны треугольник ABC.
Подсказка 3
Точка F пока что "витает в воздухе". Что хочется провести, чтобы иметь возможность "перенести" отношение AK : KC?
Подсказка 4
Проведите через F прямую, параллельную AC. Тогда можно будет посчитать углы и найти, например, равнобедренные треугольники!
Найдем стороны треугольника Треугольники
и
подобны, откуда:
Подставим и получаем квадратное уравнение относительно
Треугольники и
подобны:
Аналогично подставим и решим уравнение:
Тогда из теоремы Пифагора для прямоугольных треугольников найдем катеты:
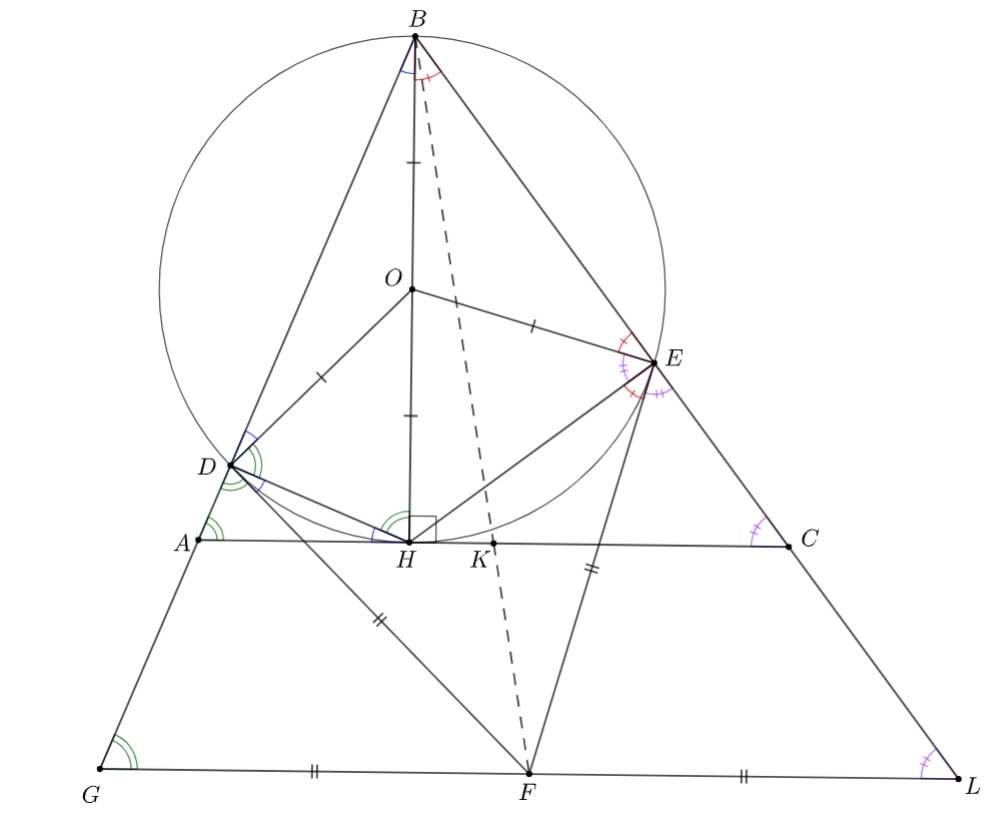
Найдем отношение Проведем через
прямую параллельную
обозначим точки пересечения продолжения сторон
и данной прямой
Пусть
— центр окружности. Тогда:
Треугольник равнобедренный,
Аналогично, треугольник
равнобедренный,
По свойству
касательных
поэтому
Следовательно,
— медиана треугольника
Треугольники
и
подобны,
— медиана треугольника
Таким образом:
Найдем длину Медиана треугольника
по формуле длины медианы:
Найдем длину
По теореме косинусов:
Тогда:
Ошибка.
Попробуйте повторить позже
Сотовая связь — это целый мир возможностей. Но чтобы пользоваться ими, нужно быть в зоне действия базовой станции. Сети GSM (2G) имеют мощность, которая позволяет покрывать территорию радиусом до 35 километров на открытой местности. В городских условиях, где много зданий, зона приема сигнала значительно уменьшается. Сети 3G и 4G (LTE) работают на более высоких частотах, чем сети 2G, и их сигнал хуже проникает сквозь препятствия и больше подвержен помехам. В сетях GSM было достаточно нескольких вышек, чтобы покрывать большие территории, а для 3G и 4G сетей для обеспечения надежной связи требуется больше вышек.
В городе установлен ретранслятор GSM сети, который обеспечивает покрытие в пределах окружности радиусом км. Центр
окружности — основание вышки. Однако из-за особенностей рельефа зона покрытия этого ретранслятора ограничена хордой, проведенной
внутри этой окружности. Хорда находится на расстоянии
км от центра окружности.
В меньшем сегменте, образованном хордой, необходимо установить два дополнительных ретранслятора (3G вышки) так, чтобы их зоны
покрытия касались друг друга, хорды и основной окружности. Каждый из этих ретрансляторов имеет круговую зону покрытия одинакового
радиуса
Найдите радиусы зон покрытия двух дополнительных ретрансляторов, которые нужно установить в меньшем сегменте. Определите площадь части меньшего сегмента, которая не попадает в зону действия дополнительных ретрансляторов.
Источники:
Подсказка 1
Изобразим условие на рисунке. Пусть O — центр окружности, в радиусе которой действует GSM вышка, AB —хорда, OP = d — расстояние от основания вышки до хорды, C и D — основания 3G вышек. Что можно сказать про их расположение, исходя из условия?
Подсказка 2
Верно! Они касаются прямой OP в одной точке (пусть K)! Проведём радиусы в точки касания. Какая теорема поможет найти нам радиус малых окружностей?
Подсказка 3
Конечно! Давайте применим теорему Пифагора для △OCK, предварительно выразив отрезки OC и OK через радиус малой окружности и данные в условии величины. А что делать с площадью части меньшего сегмента, которая не попадает в зону действия вышек?
Подсказка 4
Введите угол с вершиной O и выразите искомую площадь, равную разности площадей сегмента и площади, которую покрывают 3G вышки.
Подсказка 5
△OPA — прямоугольный. Пусть ∠POA = α. Тогда cos(α)=OP/OA = d/R — известное нам отношение! Значит через этот угол можно выразить нужные нам площади! Осталось только аккуратно посчитать и записать ответ!
Пусть вышки имеют одинаковый радиус действия
Радиус основной окружности
расстояние от центра большой окружности до
хорды
Введем точки, как показано на чертеже:
— центр большой окружности,
— центры маленьких окружностей,
—
точка касания маленьких окружностей,
— точка касания окружности с хордой.
— заданное расстояние от центра до хорды
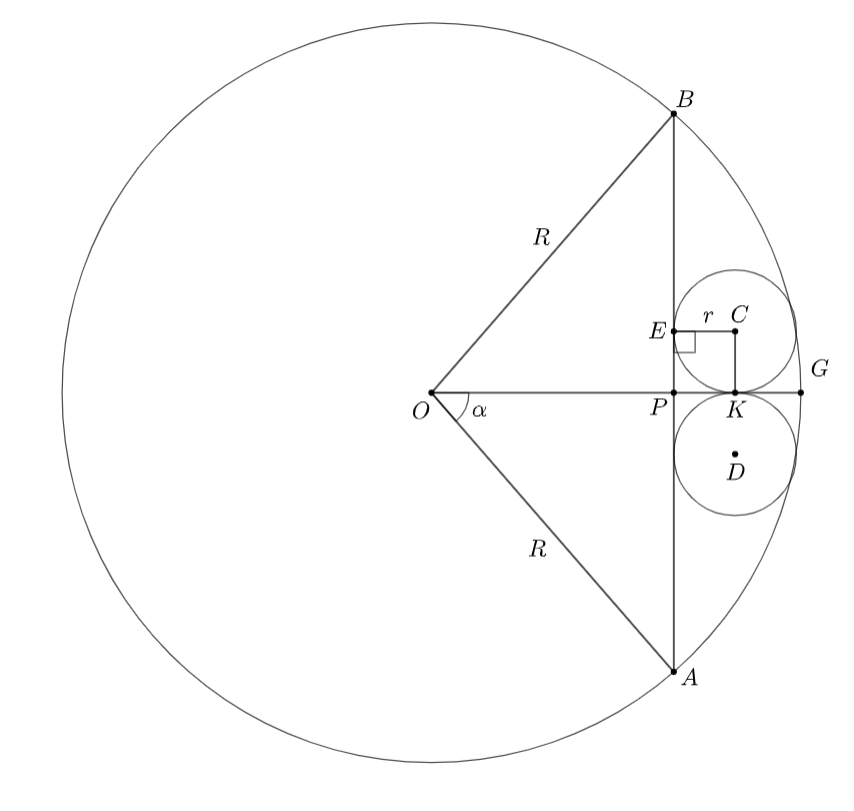
Тогда из рисунка понимаем следующие вещи:
Запишем теорему Пифагора для и выразим меньший радиус:
Подсчитаем площадь части сегмента, которая не попадает в зону действия ретрансляторов
Пусть
Выразим нужные нам синусы и косинусы углов, а потом посчитаем нужную площадь как разность:
Подставим значения
Итого, подставив все значения, получаем конечный ответ:
Ошибка.
Попробуйте повторить позже
Газонная поливалка равномерно разбрызгивает вокруг себя воду в круге радиуса На границе этого круга расположена другая
такая же поливалка. А ровно посередине между двумя поливалками находится вход в нору. Мышь, хозяйка норы, хочет вернуться домой, но
не хочет сильно вымокнуть.
Найдите длину пути, на котором мышь намокнет меньше всего. Мышь может менять направление бега, но её скорость постоянна, и под душем двух поливалок мышь мокнет вдвое быстрее.
Источники:
Подсказка 1
Давайте инвертируем путь мышки (т.е. представим, что мышка наоборот выбегает из норы). Очевидно, что ответ от этого никак не поменяется, а решать задачу будет проще. Хорошо, тогда часть своего пути мышь пробежит под двумя поливалками, а другую часть — только под одной.
Подсказка 2
Давайте попробуем чем-нибудь параметризировать траекторию, по которой бежит мышка. Ага! Мы можем задать траекторию бега мышки единственной точкой — точкой, в которой мышь выбегает из зоны двух поливалок. Назовём эту точку H. До (⋅) H мышке выгодней бежать по прямой, а дальше по радиусу одной из окружностей.
Подсказка 3
Пусть (⋅)A и (⋅)B — центры окружностей. Очевидно, что положение (⋅)H определяется углом ∠HAB, а также через этот угол и радиусы окружностей можно записать функцию, описывающую расстояние, которое пробежит мышка!
Подсказка 4
Запишем эту функцию, затем возьмём её производную и найдём локальный экстремум. Также не забываем, в каком диапазоне у нас может меняться ∠HAB! Проверим, что мы нашли именно минимум и найдём соответствующее ему расстояние.
Пусть радиус полива равен В точках
и
расположены поливалки, нора находится в
Поменяем направление — пусть
мышь выбегает из норы и стремится на сухую землю. Путь мыши может быть какой угодно формы, но, так или иначе,
ей придётся покинуть область двойного полива — пусть это произойдёт в точке
Тогда оптимальный путь до точки
— это отрезок
а оптимальный путь от
до сухой земли — это
где
лежит на радиусе
Значит,
кандидаты на оптимальный путь — ломаные вида
и определяются они одним параметром — положением точки
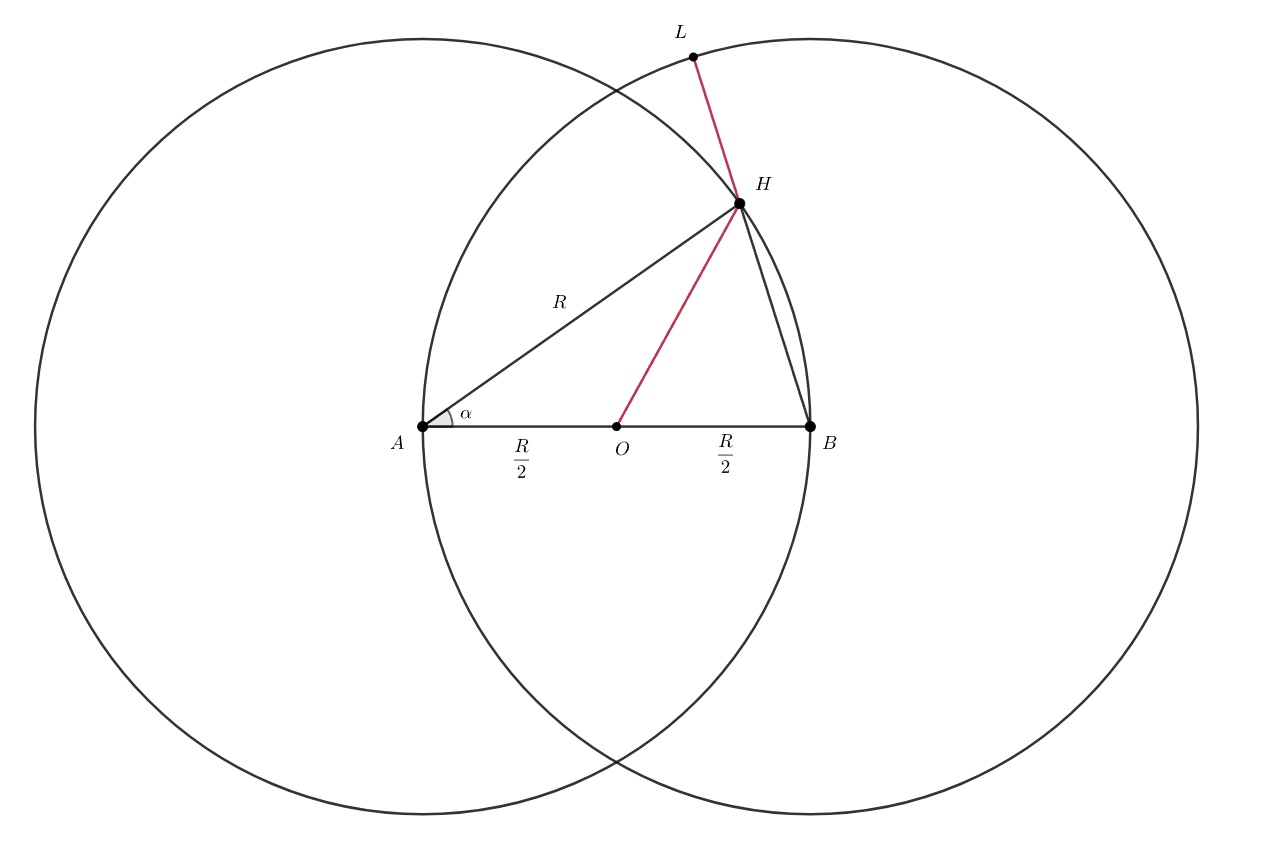
Мышь мокнет от каждой поливалки, поэтому нужно минимизировать сумму расстояний, пройденных под каждой поливалкой. Путь под
поливалкой равен
путь под поливалкой
равен
поэтому нужно найти минимально возможное значение
Опишем положение через угол
где
Тогда:
По теореме косинусов:
Далее, а
найдём как основание равнобедренного треугольника с боковыми сторонами
и известным углом
между ними:
Значит:
Нужно найти минимум функции которая характеризует степень намокания — берём производную:
Нулю может равняться только скобка (угол меняется в таких пределах, что
в ноль не обращается). Решаем
уравнение:
Если то
Значит, экстремум равен:
На всякий случай проверим, точно ли это точка минимума. Если бы мышь взяла курс ровно наверх, то приняла бы значение
что больше, чем
Если бы побежала направо —
равнялось бы
Так что мы действительно нашли
минимум.
Длина пути при этом равна:
Ошибка.
Попробуйте повторить позже
В прямоугольной трапеции меньшая диагональ равна большей боковой стороне. Найдите большую диагональ, если большая боковая сторона
равна а меньшее основание равно
Пусть — большая боковая сторона трапеции
— меньшее основание,
— большая диагональ.
Опустим перпендикуляр
на большее основание
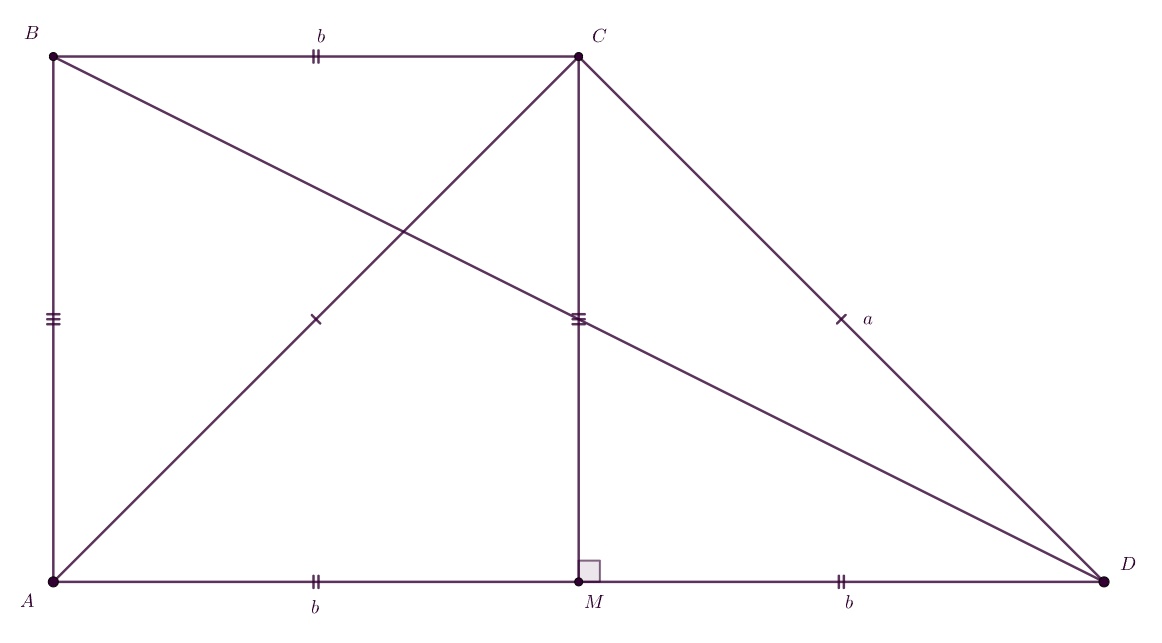
Поскольку то
а так как
то
Значит,
Следовательно,
Ошибка.
Попробуйте повторить позже
Дизайнер спроектировал офисное помещение с основанием в виде прямоугольного треугольника угол
прямой. С помощью
потолочного освещения помещение разбито на зоны следующим образом: большой светильник
освещает площадь
ограниченную
окружностью, которая вписана в треугольник
Если к этой окружности провести внутри треугольника
касательные,
параллельные сторонам комнаты, то получатся еще три треугольника при вершинах
и
в которые можно вписать
маленькие окружности, ограничивающие площади
Эти площади освещаются дополнительными светильниками
Найдите, радиусы всех окружностей и освещенность каждой зоны, если площадь треугольника равна кв.м,
гипотенуза
м, величина угла
меньше величины угла
а показатели световой отдачи (яркости)
светильника
составляет
лм, светильника
лм, светильника
лм и светильника
лм.
Освещенность площади
светильником
с показателем световой отдачи
рассчитывается по формуле
(лк),
где
поправочный коэффициент, лк — люкс, лм — люмен.
Источники:
Подсказка 1
Вообще вся задача про счёт, бояться его не нужно. Вспомните формулу площади, в которой фигурирует радиус.
Подсказка 2
Не забывайте, что напротив меньшего угла лежит меньшая сторона.
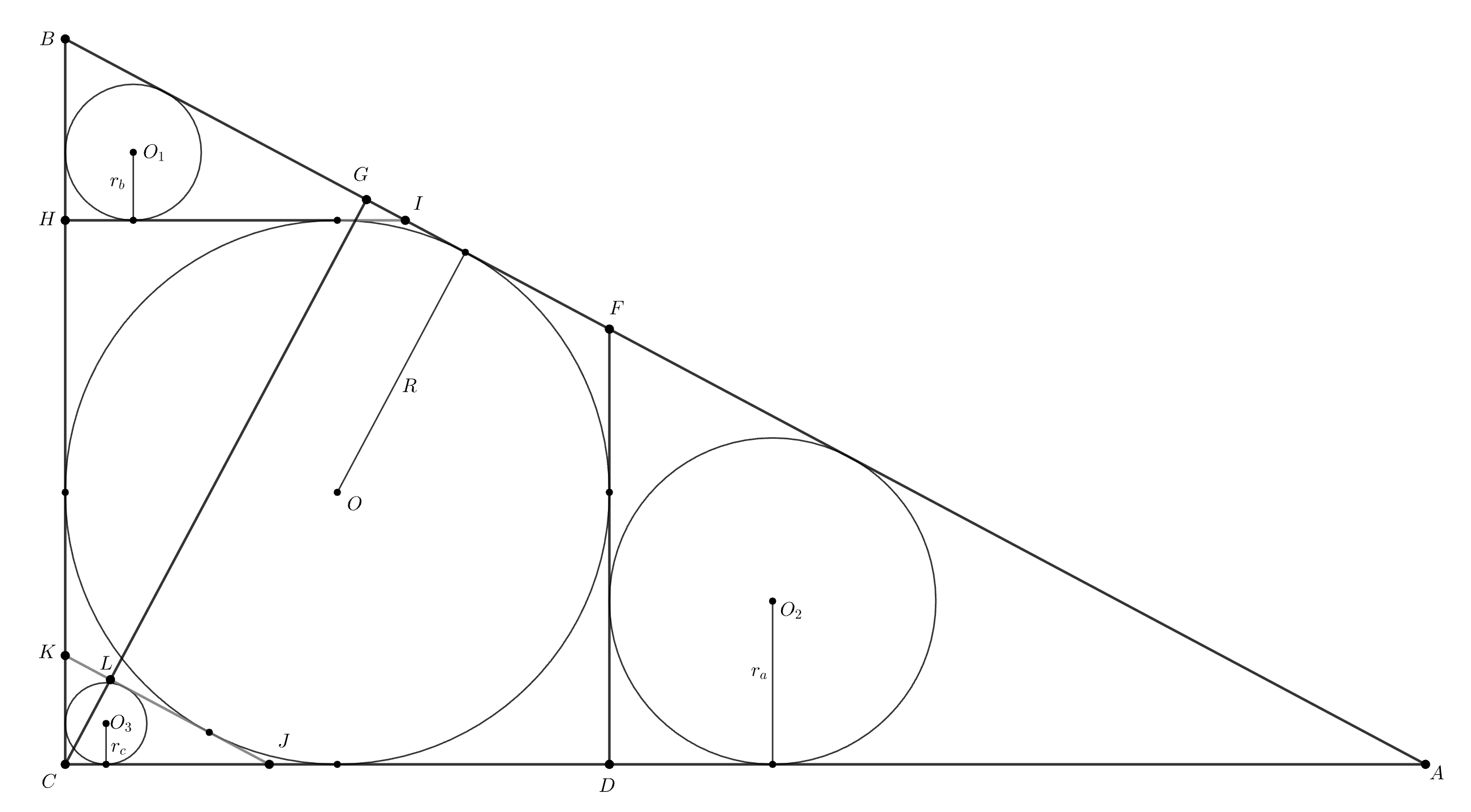
В треугольник вписана окружность с центром
пусть ее радиус равен
пересекается с
в точке
Центрами вписанных окружностей треугольников
и
будут
и
их
радиусы —
и
С другой стороны, если и
— катеты, а
— гипотенуза треугольника
то
Тогда
Теперь
Тогда и
или
и
Напротив меньшего угла лежит меньшая сторона, поэтому
Маленькие треугольники подобны большому треугольнику, т.к. стороны параллельны. Расстояние между проведенными параллельными
прямыми и соответствующими им сторонами равно диаметру большого круга. Поэтому
Площади меньших кругов равны
Вычислим освещенность:
Ошибка.
Попробуйте повторить позже
В треугольник вписана окружность радиуса
касающаяся стороны
в точке
причём
a) Докажите, что треугольник прямоугольный.
б) Вписанная окружность касается сторон и
в точках
и
Найдите площадь треугольника
если известно, что
и
а)Пусть точка — центр вписанной окружности, а точка
— точка, в которой эта окружность касается стороны
Заметим, что как радиусы окружности, и
по условию. С другой стороны,
как отрезки
касательных. Получается,
Отсюда, четырёхугольник
— ромб.
Так как касательная к окружности перпендикулярна радиусу, проведённому в точку касания, то Итак,
четырёхугольник
— ромб, у которого один из углов равен
то есть
— квадрат, откуда
и
прямоугольный.
б) Пусть Так как отрезки касательных равны, то
и
Тогда
Распишем теорему Пифагора для
Итак, Рассмотрим угол, лежащий между сторонами
и
в треугольнике
Заметим, что его синус равен
:
По формуле площади:
б) 40
Ошибка.
Попробуйте повторить позже
Все три плоских угла при вершине тетраэдра
равны
Найдите
если известно, что
и
Источники:
Обозначим Выразим
через теорему косинусов для треугольников
и
и приравняем
результаты:
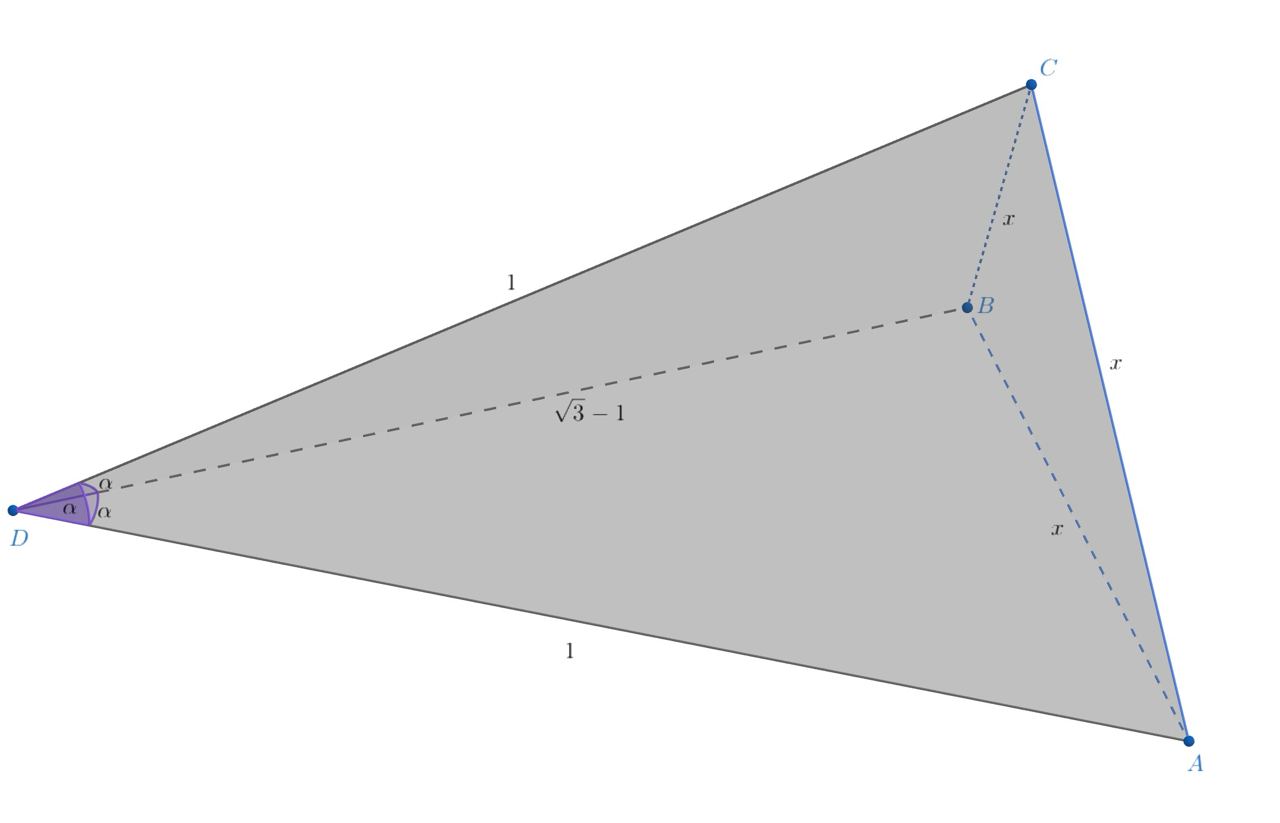
Если тогда треугольник
равнобедренный с углами
при основании. По теореме синусов
для треугольника
Отсюда получаем:
Запишем теорему косинусов для треугольника
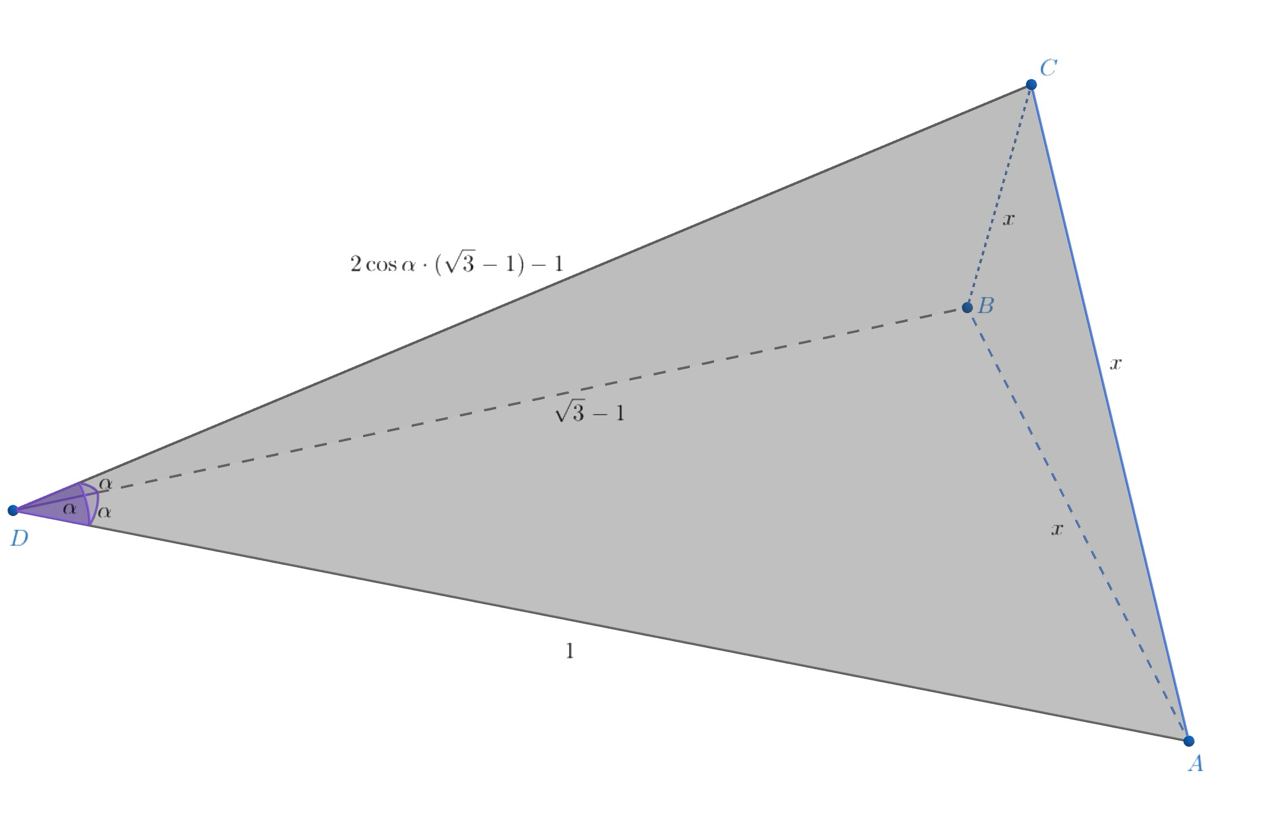
Если то
Выразим через теорему косинусов для треугольников
и
приравняем результаты:
Так как
этот корень убираем из рассмотрения.
Если
то
Сравним полученный косинус с единицей:
Так как
Это невозможно, следовательно, единственным ответом к задаче является
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике выполняются равенства:
и
Докажите, что из отрезков
и
можно сложить прямоугольный треугольник.
Пусть — точка пересечения диагоналей.
.png)
Пары треугольников и
и
подобны, поскольку каждая пара имеет общую вершину и еще один равный по
условию угол. Подобия влекут соответственно равенства
то есть
Складывая, имеем что в силу теоремы Пифагора влечет требуемое.
Ошибка.
Попробуйте повторить позже
Внутри окружности радиуса 5 отмечена точка
через которую проведены хорды
и
перпендикулярные друг другу.
Найдите все возможные значения расстояния от вершины
прямоугольника
до центра
окружности
если известно, что
Источники:
Подсказка 1
Нам ведь не просто так дана перпендикулярность, мы определенно воспользуемся ей в будущем, но как это сделать?
Подсказка 2
Скорее всего, перпендикулярность пригодится нам для теоремы Пифагора. Найти мы хотим FO, какие отрезки можно посчитать для этого?
Подсказка 3
Давайте проведем через точку O прямую, параллельную AB, тогда на этой прямой и прямой FA образуется прямоугольный треугольник с гипотенузой FO!
Подсказка 4
Все равно пока не очень понятно, как считать... Нам даны радиус и отрезок OE, но для чего?
Подсказка 5
А можно ли получить где-то равные им отрезки?
Подсказка 6
Пусть прямая, проведенная через O параллельно AB, пересекается с FA в точке X, с CE — в точке K. Обозначим KO за x, продлим KO за точку X на длину x, получим точку O₁.
Подсказка 7
Запишите теорему Пифагора для треугольников XO₁F и XAO. Можно ли выразить их через известные величины?
Подсказка 8
Сложите полученные выражения и перегруппируйте слагаемые.
Пусть расстояние от точки до прямой
равно
Проведем через точку
прямую, параллельную
на этой прямой отметим
точку
находящуюся на расстоянии
от прямой
так, чтобы точки
и
были по разные стороны от прямой
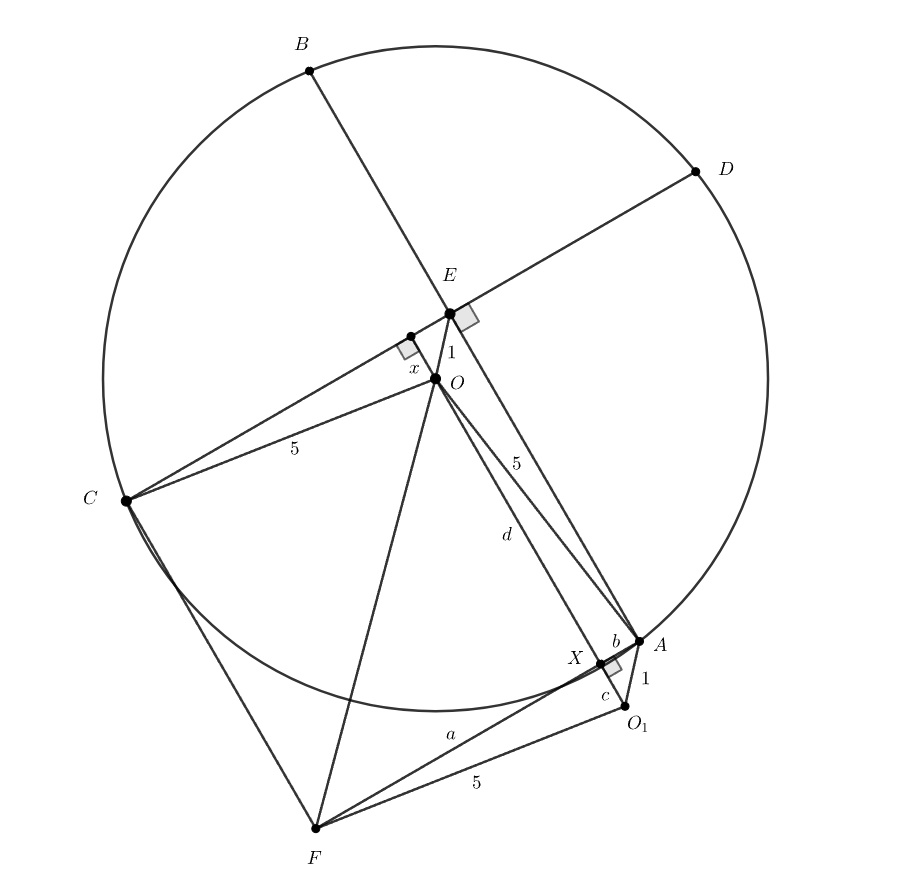
Очевидно, что и
Заметим, что диагонали четырехугольника
перпендикулярны, обозначим
точку пересечения диагоналей за
введем обозначения:
По теореме Пифагора
Отсюда можно вычислить
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике проведена высота
из вершины прямого угла
В треугольники
и
вписаны
окружности с центрами
и
соответственно, касающиеся прямой
в точках
и
соответственно.
a) Докажите, что прямые и
перпендикулярны.
б) Найдите площадь четырёхугольника , если
и
a)
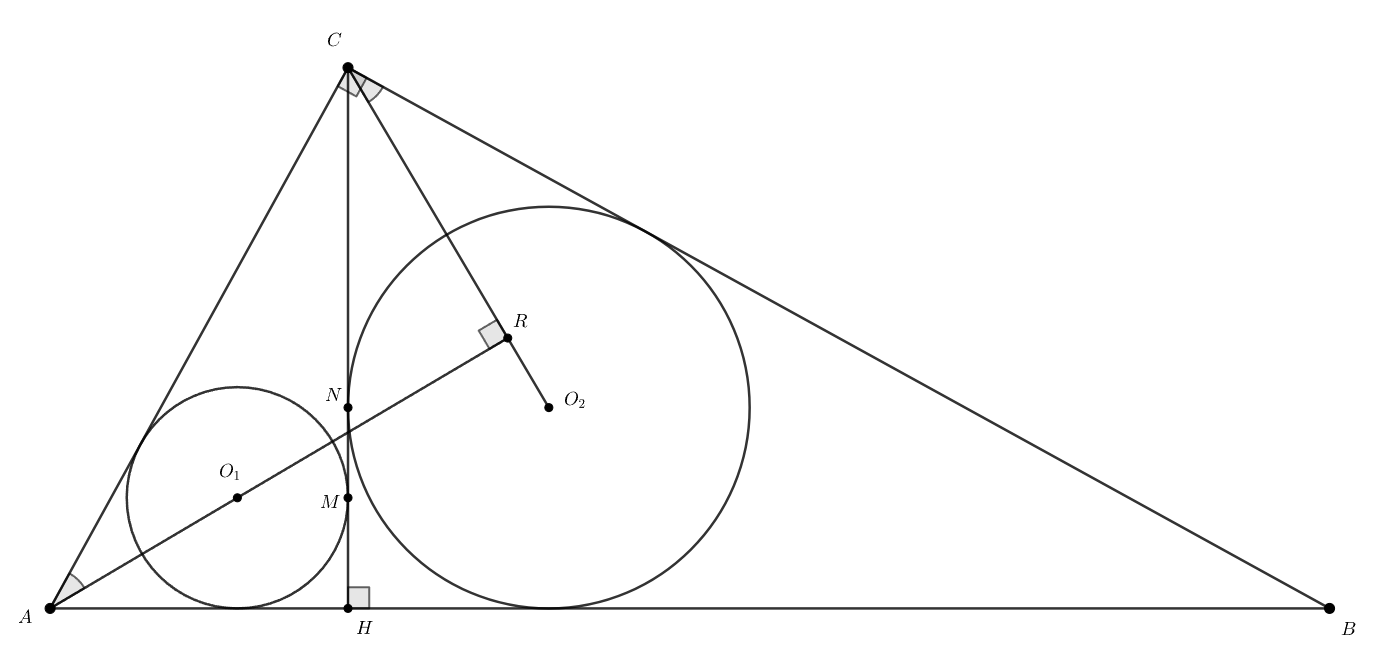
Заметим, равенство углов поэтому
Посчитаем сумму двух углов
где
— это точка
пересечения
и
б) Четырёхугольник состоит из двух прямоугольных треугольников
поэтому его площадь равна сумме
площадей. Найдём катеты этих двух треугольников.
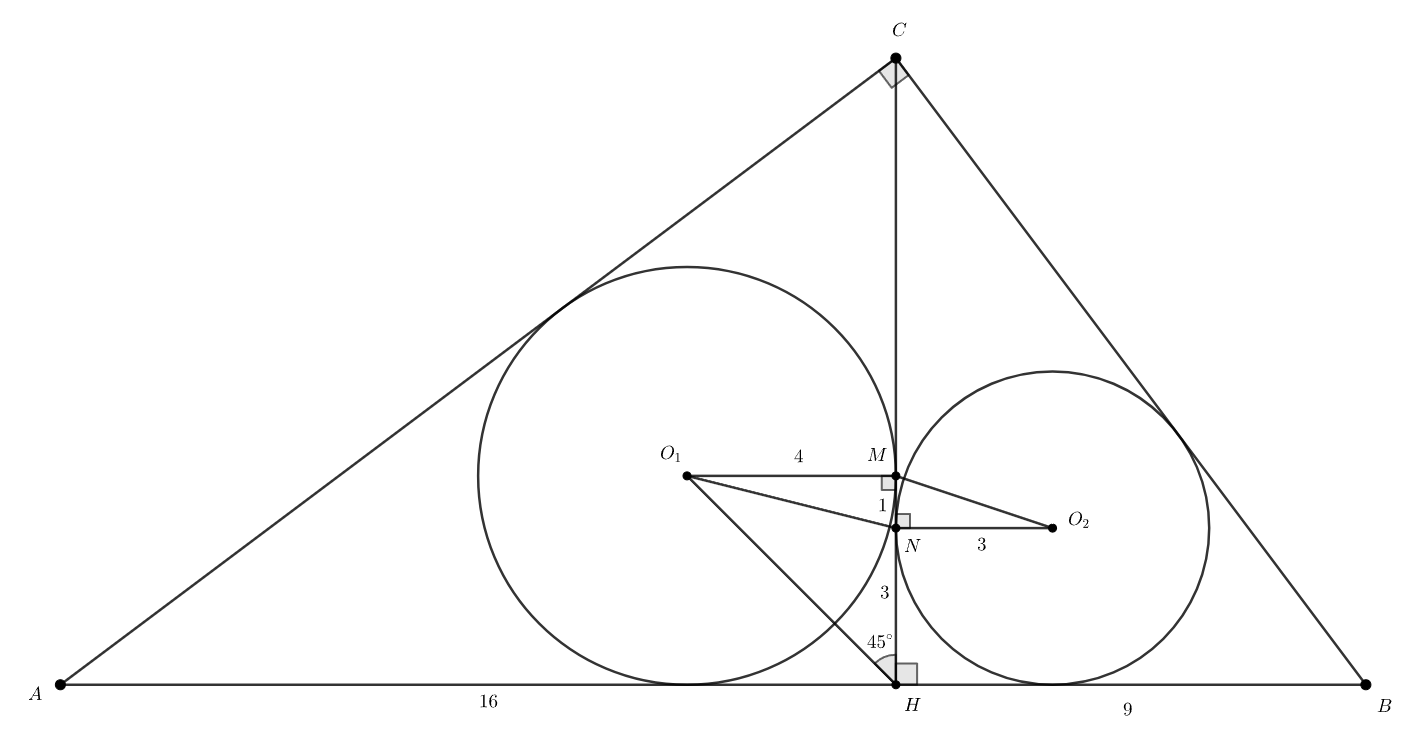
Из теоремы Пифагора для
Из формулы для высоты в прямоугольном треугольнике
Затем находим стороны и
из прямоугольных треугольников
и
Теперь нужно найти отрезки касательных:
Откуда
Осталось найти и
рассмотрим
— он прямоугольный и
таким образом он равнобедренный. Стало
быть
так же получается, что
Осталось только посчитать площадь
Ошибка.
Попробуйте повторить позже
В треугольник со сторонами
,
вписана окружность с центром в точке
, которая касается сторон
и
в точках
и
соответственно. На прямой
отмечена точка
так, что угол
равен
. Найдите длину отрезка
.
Подсказка 1
Во-первых, давайте поймём, что у нас за картинка. А картинка у нас фиксирована, то есть мы можем вычислить (возможно, с большой сердечной болью) любой объект на картинке. А значит, скорее всего, задача на счёт. При этом, если мы уже хотим считать, то давайте посчитаем углы треугольника (возможно, угол OAK равен 60 градусам неспроста, иначе, непонятно как связать его хоть с чем-то)
Подсказка 2
По теореме косинусов угол ABC равен 60 градусам. Значит, угол AOC — 120. То есть, прямые OC и AK параллельны, а где параллельность — там и подобие.
Подсказка 3
Мы знаем, что OC перпендикулярно MN. А значит, и AK перпендикулярно MN. Если OC и MN пересекаются в T, то выходит, что MTC и MAK подобны. При этом мы знаем их коэффициент подобия и сторона MT ищется, так как известен угол и можно найти отрезок касательной MC.
Подсказка 4
Мы знаем KM, а значит, так как знаем KM и MT, то знаем и KN.
Заметим сразу, что , то есть треугольник
— остроугольный. А значит,
и
. Поэтому
точка
лежит снаружи треугольника
Обозначим углы треугольника за По теореме косинусов найдем угол
Проведем . Тогда
Поэтому, так как
по условию,
Пусть — точка пересечения
и
.
— биссектриса, медиана и высота в равнобедренном треугольнике
, поэтому
![]()
Тогда из прямоугольного треугольника получаем
По теореме косинусов найдем угол
По формуле половинного угла
По основному тригонометрическому тождеству
И тогда
А из треугольника находим
В итоге
Ошибка.
Попробуйте повторить позже
В
, биссектриса
Найти длины сторон
и
.
Источники:
Подсказка 1
Обозначим неизвестные стороны за переменные, пусть АВ = с, АС = b. Тогда по свойствам биссектрисы легко посчитать BL и LC.
Подсказка 2
Данный по условию cos∠A намекает нам на теорему косинусов. Но для каких треугольников её лучше записать?
Подсказка 3
Для △ABL и для △ACL! Все стороны для теоремы косинусов посчитаны. Вопрос только с углом. Но посчитать косинусы ∠BAL и∠CAL, зная, что cos∠A = 1/8, несложно!
Подсказка 4
Теперь осталось лишь решить эту не самую красивую систему из двух уравнений. Не забывайте, что b и c не просто переменные, а стороны △ABС, значит, для них должно выполняться неравенство треугольника.
Пусть . Если обозначить
через
, а
через
, то с помощью свойства биссектрисы нетрудно вычислить
.
![]()
Вычислим .
Теперь напишем теоремы косинусов для треугольников и
:
Вычтем одно равенство из другого и получим:
Если , то имеем
Тогда либо , либо
Первый вариант неверен, потому что тогда не будет выполняться неравенство треугольника . При втором варианте не
выполняется теорема косинусов для треугольника
Значит,
Решая это уравнение как квадратное относительно получаем
. Подставляя это в первое уравнение,
получаем
Этим значениям соответствуют
Ошибка.
Попробуйте повторить позже
Меньшая сторона параллелограмма и меньшая его диагональ, соответственно равные и
образуют угол в
Найдите
радиус описанной окружности около четырёхугольника, образованного пересечениями биссектрис внешних углов заданного
параллелограмма.
Источники:
Подсказка 1
С такой информацией в дано грех не найти длину отрезка AD, используя теорему косинусов.
Подсказка 2
Теперь разберёмся с четырёхугольником, образованным пересечениями биссектрис. Для этого стоит вспомнить, чему равен угол между биссектрисами односторонних углов.
Подсказка 3
Пусть MN — внешняя биссектриса угла B (точки M и N на описанной окружности). Аналогично определим прямую NP для угла C. Пересечём эти прямые с AD в точках L и F. Рассмотрите трапецию LBCF. Чем для этой трапеции будет являться отрезок MP? :)
Пусть — заданный параллелограмм. Тогда
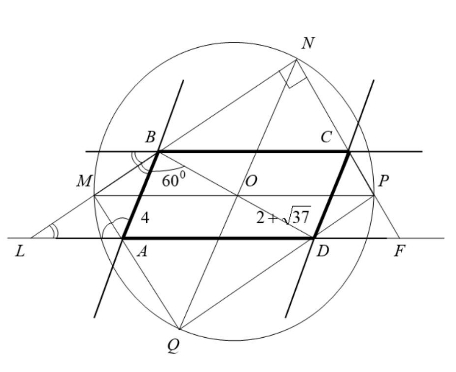
По теореме косинусов в
Пусть биссектрисы внешних углов при вершинах и
параллелограмма
пересекаются в точке
биссектрисы внешних
углов при вершинах
и
— в точке
углов при вершинах
и
— в точке
а углов при вершинах
и
— в точке
Четырехугольник, образованный биссектрисами внешних углов параллелограмма, есть
Биссектрисы односторонних углов при параллельных прямых и секущей пересекаются под прямым углом, а значит, —
прямоугольник
Пусть биссектриса внешнего угла пересекает продолжение стороны
в точке
Рассмотрим
— равнобедренный (так как
— биссектриса и накрест лежащие углы при параллельных прямых
и
и секущей
равны), то
и
биссектриса
является и медианой, то есть
— середина
Аналогично, в равнобедренном и
— середина
Рассмотрим трапецию
в которой MP
является средней линией, а значит, она параллельна основаниям и равна:
По заданным числовым значениям задачи получаем: Итак,
— прямоугольник, где диагонали
и радиус описанной около прямоугольника окружности равен
Ошибка.
Попробуйте повторить позже
В четырехугольнике два противоположных угла прямые, а диагонали перпендикулярны друг другу. Докажите, что одна из них делит другую пополам.
Обозначим наш четырёхугольник Пусть
— точка пересечения диагоналей. Докажем, что
По теореме
Пифагора
Запишем таким образом:
Аналогично Осталось заметить, что по теореме Пифагора
Это даёт
равенство
и
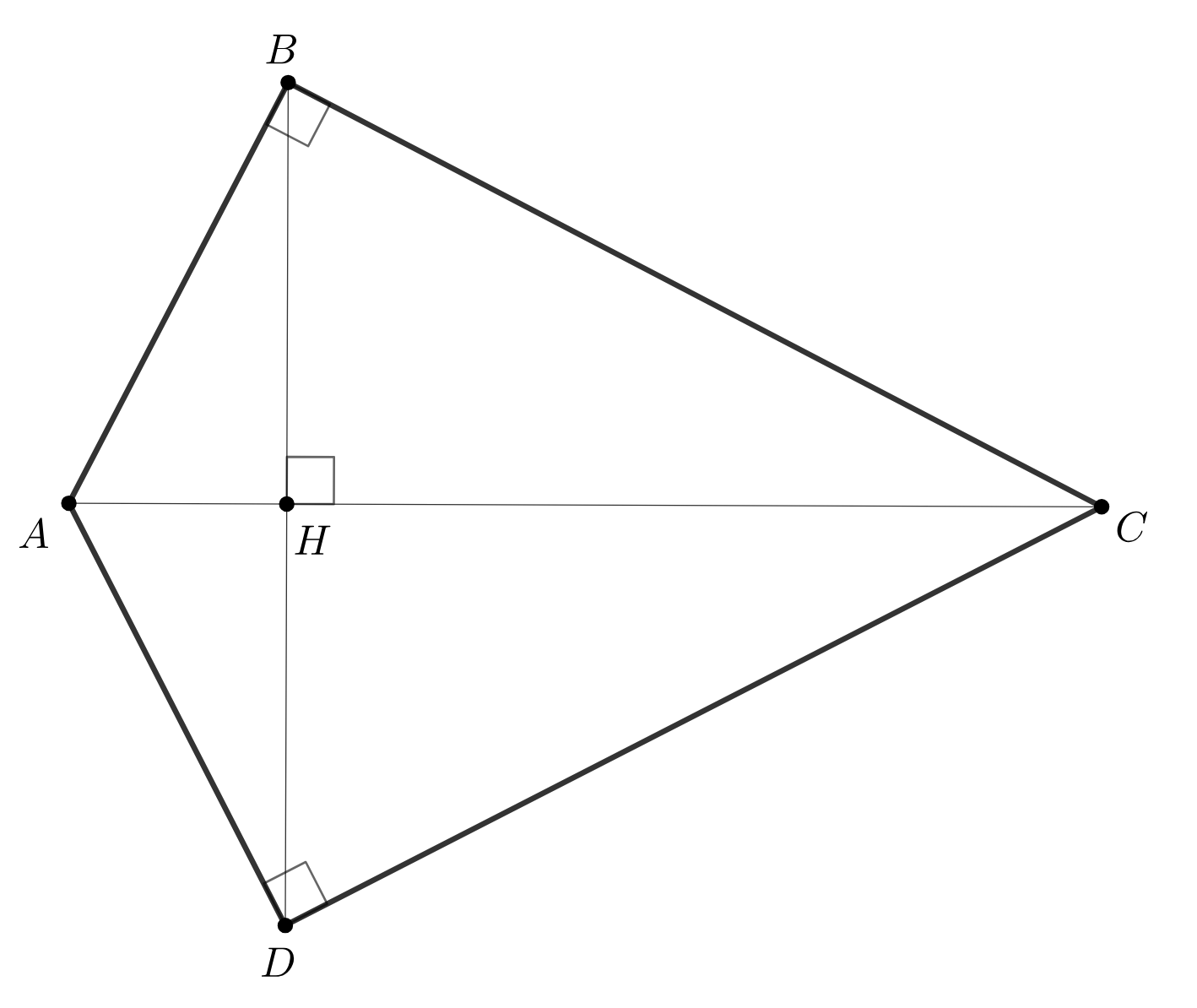
Ошибка.
Попробуйте повторить позже
Прямая, параллельная биссектрисе треугольника
проходящая через середину
его стороны
пересекает
сторону
и продолжение стороны
в точках
и
соответственно. Найдите
если
Источники:
Подсказка 1
Нетрудно заметить, что BC = 2BM = 2CM. Значит, мы можем найти какую-то из сторон BM и CM, а потом и BC. Какое дополнительное построение можно сделать?
Подсказка 2
Попробуем провести среднюю линию MN, параллельную стороне AB. Здесь уже можно заметить подобные треугольники и найти какие-то равные углы или стороны. Какие?
Подсказка 3
Нам интереснее всего посмотреть на равнобедренный треугольник AYZ, подобный YNM, и найти в нем какие-то углы, стороны. А отсюда сможем найти и NM из треугольника YNM.
Подсказка 4
Посмотрим на треугольник CNM: в нем мы знаем две стороны. Что еще мы можем в нем найти?
Подсказка 5
Мы можем выразить косинус угла между найденными сторонами, так как из треугольника AYZ уже знаем косинус половинного угла. Значит, мы можем применить теорему косинусов и найти CM, а это именно то, что нам нужно!
Обозначим Тогда
за счёт параллельности
и
получаем
Пусть — средняя линия треугольника
параллельная стороне
Тогда В треугольниках
и
есть по два угла, равных
Значит, они оба равнобедренные и подобны
друг другу. Из треугольника
находим, что
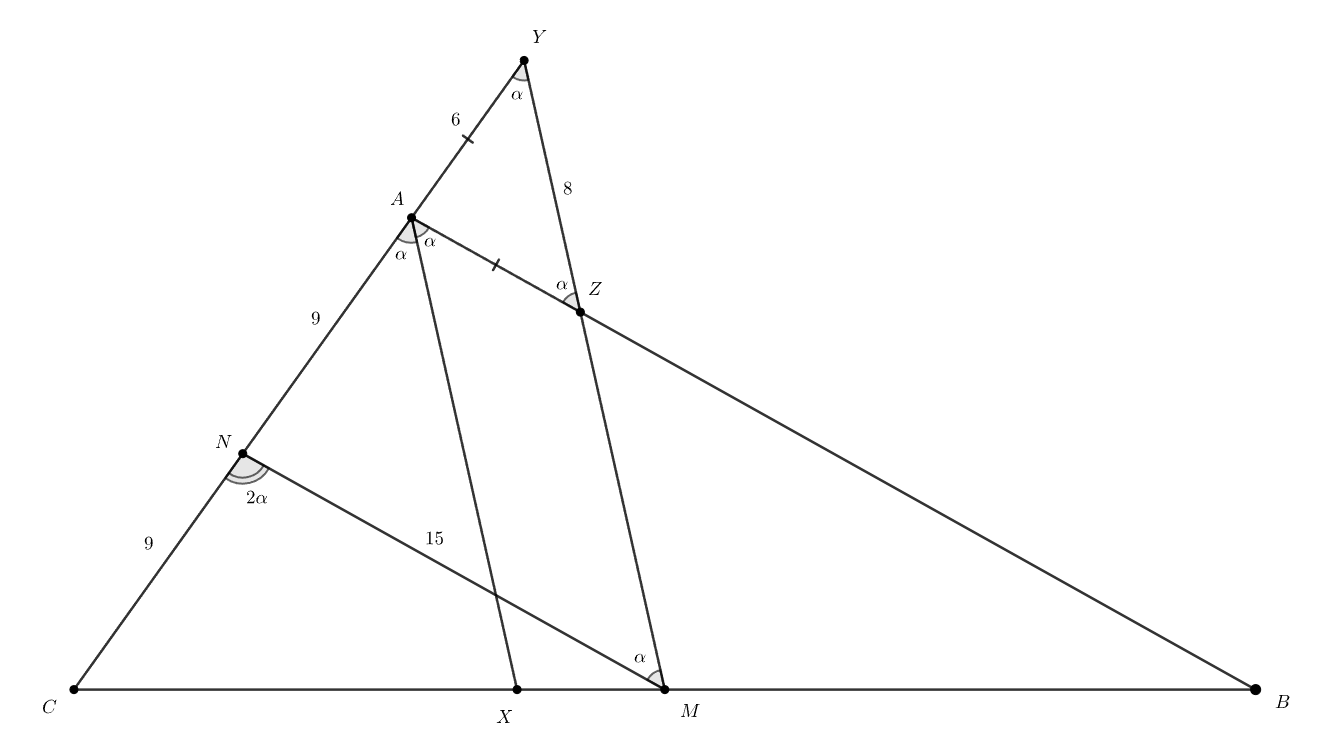
Заметим также, что как внешний угол треугольника
Кроме того,
По теореме косинусов для треугольника получаем:
Ошибка.
Попробуйте повторить позже
Окружность с диаметром касается сторон угла
в точках
и
Её хорда
проходит через середину хорды
а отрезок
пересекает окружность в точке
а) Докажите, что хорды и
параллельны;
б) Найдите отношение если угол
равен
Источники:
Пункт а, подсказка 1
Внимательно посмотрите на чёртеж: что мы могли бы сказать про точки E и F, если бы условие задачи выполнялось?
Пункт а, подсказка 2
Заметим, что вся картинка симметрична относительно прямой AO. Тогда нам нужно доказать, что точки E и F тоже симметричны относительно этой прямой! Но как это сделать?
Пункт а, подсказка 3
Пусть N — точка, диаметрально противоположная точке C. Тогда точки A, E и N должны лежать на одной прямой! Что это говорит нам об углах нашего чертежа?
Пункт а, подсказка 4
Угол CEN прямой, значит, угол CEA тоже должен быть прямым. Чтобы это доказать, найдите вписанный четырёхугольник на чертеже!
Пункт б, подсказка 1
На картинке много равных и прямых углов, что может намекать нам на обилие подобных треугольников! Из какого подобия мы можем достать нужное отношение?
Пункт б, подсказка 2
Пусть M — середина BC. Заметим, что треугольники MFE и MDN подобны! Это подобие даёт нам отношение некоторых сторон.
Пункт б, подсказка 3
Более того, одно из этих отношений — искомое, а второе мы можем найти, используя теорему Пифагора и степень точки M!
а) Пусть середина
точка диаметрально противоположная
Докажем,что точки
и
симметричны относительно
прямой
для этого достаточно чтобы
и
лежали на одной прямой.
Так как, диаметр, то достаточно доказать, что
Но так, как
то хотим доказать, что
лежат на одной окружности, для этого проверим, что
Заметим, что вписанный,
лежит на прямой
и
вписанный, поэтому верны следующие равенства
б) Можно считать, что Заметим,что
Значит,из теоремы косинусов Так же видно, что
Наконец, заметим, что
и
подобен
поэтому
Это отношение и посчитаем. Посчитаем с помощью теоремы Пифагора, для
где
— середина
Воспользуемся степенью точки
Откуда получаем
Посчитаем нужное отношение
Ошибка.
Попробуйте повторить позже
В треугольнике медиана, проведённая из вершины
в четыре раза меньше стороны
и образует с этой стороной угол
Найдите угол
Обозначим медиану из вершины через
Первое решение.
Опустим перпендикуляр на прямую
Тогда в прямоугольном треугольнике
катет
равен половине гипотенузы
так как лежит напротив угла в
градусов. А ещё по условию
Тогда
Получили, что в четырёхугольнике
диагонали точкой пересечения
делятся пополам, а значит, это параллелограмм, так что
В итоге
![]()
Второе решение.
Отметим ещё середину — как
а середину
— как
Тогда
а ещё по условию
Так что
треугольник
— равносторонний (
) с углом при вершине
в
значит, он равносторонний.
Тогда как смежный с углом в
Далее,
поэтому треугольник
— прямоугольный, и
Смежный с ним
С другой стороны, этот же угол равен
так как
— средняя линия
треугольника
— параллельна
![]()
Третье решение.
Не будем думать и просто посчитаем:
1) по теореме косинусов для треугольника
2) по формуле медианы (при удвоение медианы получается параллелограмм, у которого сумма квадратов диагоналей равна сумме квадратов всех сторон)
3) по теореме косинусов для треугольника
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике из вершины прямого угла
проведена биссектриса, которая вторично пересекает описанную
окружность треугольника
в точке
Найдите радиус вписанной в треугольник
окружности, если известно, что
, а
Подсказка 1
Середина дуги и центр вписанной окружности явно на что-то намекают... О каких отрезках и точках мы точно можем что-то сказать?
Подсказка 2
Точка I лежит на BW, а еще можно применить лемму о трезубце! Значит, мы можем посчитать BI, а еще мы знаем угол WBK...как тогда найти радиус?
Подсказка 3
Опустим перпендикуляр из I на BA и в прямоугольном треугольнике найдем один из катетов, который и является радиусом. Осталось лишь найти площадь. Т.к. нам известен радиус вписанной окружности, было бы хорошо найти площадь ровно через него. Но для этого нужен полупериметр. Как будем искать?
Подсказка 4
Вспоминаем связь полупериметра и IA (расстояние от центра вписанной окружности до вершины треугольника), IA = p - AC (p - полупериметр), а найти AC несложно, зная WA и WC.
Первое решение.
Пусть — центр вписанной в
окружности. Тогда по лемме о трезубце
Значит,
Пусть — точка касания вписанной окружности стороны
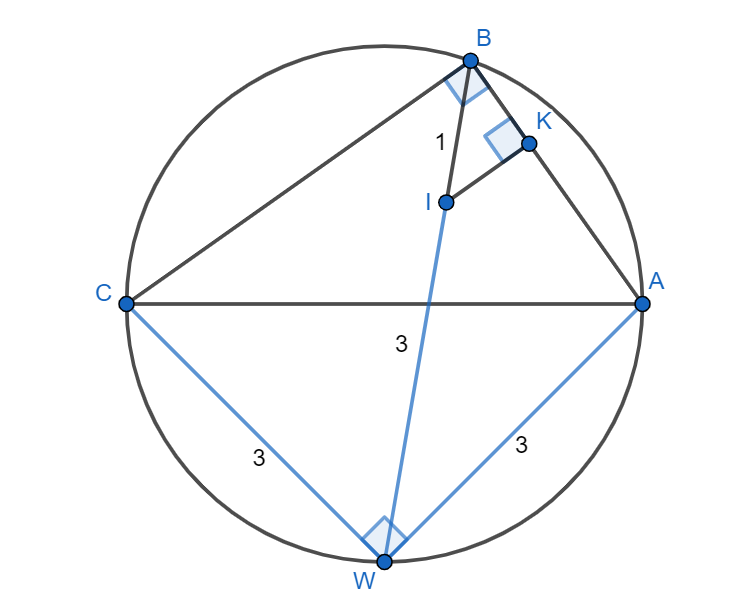
Из прямоугольного треугольника
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
как хорды, опирающиеся на равные углы. Из равнобедренного прямоугольного треугольника
находим
По теореме косинусов для треугольников и
стороны
и
являются корнями уравнения
Отсюда, используя формулу разности квадратов, получаем
В итоге
Ошибка.
Попробуйте повторить позже
Биссектрисы внешних углов треугольника
пересекают продолжения противоположных сторон треугольника в
точках
соответственно. Найдите угол
и длину отрезка
если
а угол
равен
Источники:
Подсказка 1
Мы знаем, что биссектрисы в треугольнике пересекаются в одной точке. Попробуйте провести аналогичное доказательство к тому, что эти три точки на самом деле лежат на одной прямой)
Подсказка 2
Для этого попробуйте также записать всякие отношения и теорему Менелая!
Подсказка 3
Мы поняли, что эти три точки на одной прямой, а значит искомый угол = 180 градусов. Теперь давайте перейдем к отрезку A₁B₁. Для начала можно поискать все что можно в треугольнике ABC, например, недостающую третью сторону)
Подсказка 4
Да, это можно сделать с помощью теоремы косинусов! А теперь попробуйте опять же записать множество отношений и некоторые отрезки представить в виде суммы отрезков. С этой технической работой можно дойти до нужного отрезка!
Обозначим
Треугольники и
имеют общую высоту из общей вершины
следовательно, можем записать следующие соотношения
для их площадей
| (1) |
Пусть — перпендикуляр из
к прямой
— перпендикуляр из
к прямой
Так как
—
биссектриса
значит, точка
равноудалена от прямых
и
Следовательно,
Благодаря этому
получаем
| (2) |
Из соотношений (1) и (2) следует, что
Аналогично получаем
Тогда
Значит, по теореме Менелая точки лежат на одной прямой. Т.е.
и
![]()
По теореме косинусов найдём
Теперь найдём
Аналогично получаем и
Обозначим
Получим значения
и
из двух теорем
косинусов
Запишем теорему косинусов в
Углы и
равны как вертикальные. Запишем теорему косинусов в
Следовательно,



