Теорема косинусов и теорема Пифагора
Ошибка.
Попробуйте повторить позже
Прямая, параллельная биссектрисе треугольника
проходящая через середину
его стороны
пересекает
сторону
и продолжение стороны
в точках
и
соответственно. Найдите
если
Источники:
Подсказка 1
Нетрудно заметить, что BC = 2BM = 2CM. Значит, мы можем найти какую-то из сторон BM и CM, а потом и BC. Какое дополнительное построение можно сделать?
Подсказка 2
Попробуем провести среднюю линию MN, параллельную стороне AB. Здесь уже можно заметить подобные треугольники и найти какие-то равные углы или стороны. Какие?
Подсказка 3
Нам интереснее всего посмотреть на равнобедренный треугольник AYZ, подобный YNM, и найти в нем какие-то углы, стороны. А отсюда сможем найти и NM из треугольника YNM.
Подсказка 4
Посмотрим на треугольник CNM: в нем мы знаем две стороны. Что еще мы можем в нем найти?
Подсказка 5
Мы можем выразить косинус угла между найденными сторонами, так как из треугольника AYZ уже знаем косинус половинного угла. Значит, мы можем применить теорему косинусов и найти CM, а это именно то, что нам нужно!
Обозначим Тогда
за счёт параллельности
и
получаем
Пусть — средняя линия треугольника
параллельная стороне
Тогда В треугольниках
и
есть по два угла, равных
Значит, они оба равнобедренные и подобны
друг другу. Из треугольника
находим, что
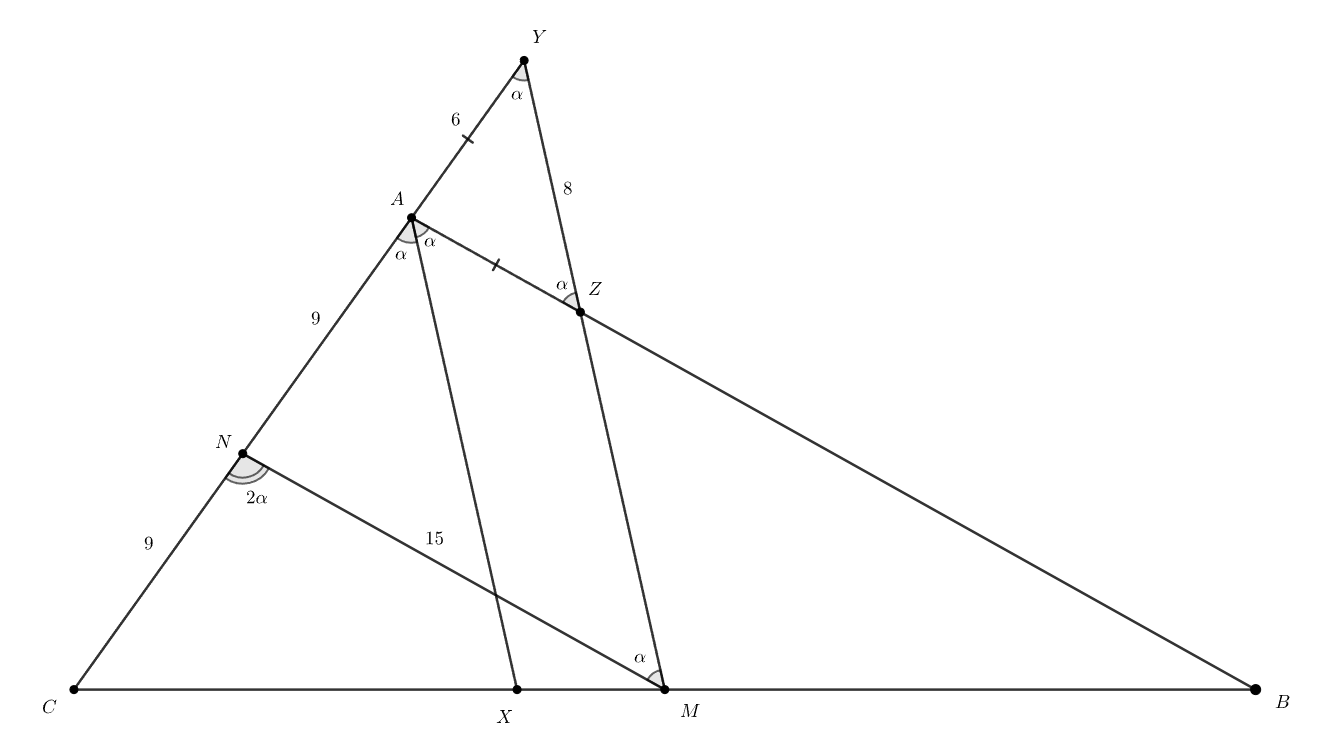
Заметим также, что как внешний угол треугольника
Кроме того,
По теореме косинусов для треугольника получаем:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




