Введение векторов или координат в планиметрии
Ошибка.
Попробуйте повторить позже
На координатной плоскости построена фигура состоящая из всех точек, координаты которых удовлетворяют неравенству
Фигуру
непрерывно повернули вокруг начала координат на угол
против часовой стрелки.
Найдите площадь множества
которое замела фигура
при этом повороте.
Источники:
Подсказка 1
Как можно упросить исходное уравнение?
Подсказка 2
Сделайте замену u = y - 20; v = x / (2√3).
Подсказка 3
Заметьте симметрию в получившемся неравенстве: если пара (u,v) ему удовлетворяет, тогда пары (-u,v), (u,-v), (-u,-v) - тоже подойдут.
Подсказка 4
Окажется, что неравенство определяет квадрат (u,v), в котором -4 ≤ u ≤ 4, -4 ≤ v ≤ 4.
Подсказка 5
После обратной замены окажется, что Ф — прямоугольник с центром в (15/2; 0). Найдите прямые, на котором лежат его стороны.
Подсказка 6
Изобразите множество М, которое заметет фигура Ф. У Вас должны получиться 2 дуги, по большей из которых "едут" точки фигуры Ф. Попробуйте что-нибудь посчитать на рисунке.
Сделаем замену:
Тогда первое неравенство имеет вид
Если пара удовлетворяет данному неравенству, то и пары
ему удовлетворяют, поэтому на
координатной плоскости неравенство задаёт множество, симметричное как относительно обеих координатных осей, так и относительно
начала координат.
Но при положительных неравенство эквивалентно
то есть при
и
при
В итоге получаем, что неравенство определяет квадрат
в котором
Значит, после обратной замены приходим к тому, что фигура — прямоугольник с центром в точке
стороны которого лежат на
прямых
Множество которое замела фигура
изображено на рисунке.
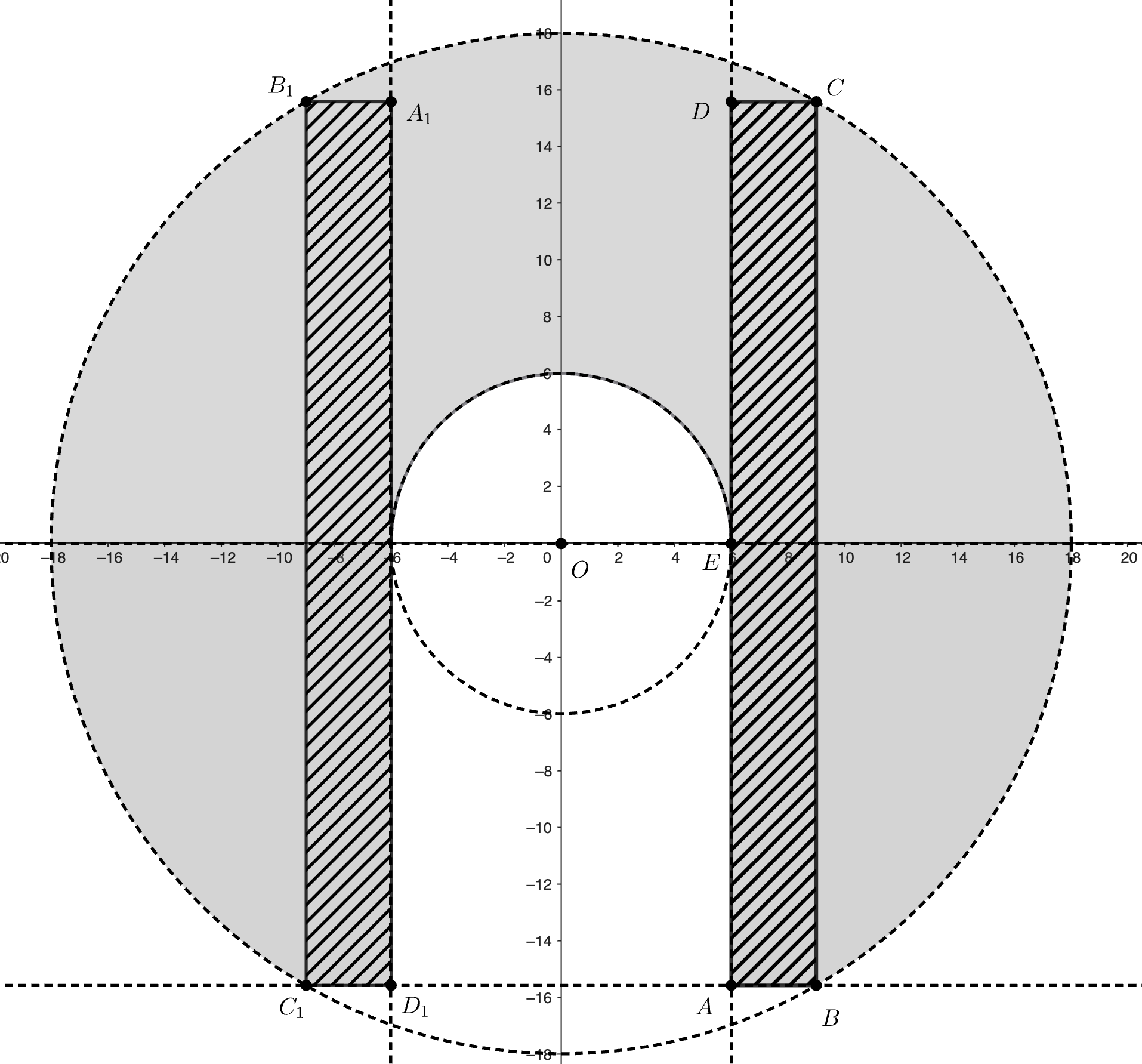
По теореме Пифагора
Тогда
Искомая площадь М складывается из разности площадей двух полукругов (она будет равна площади
прямоугольника
и площади сегмента с меньшей дугой
(две половины равных прямоугольников и равных сегментов не
попадают в разность полукругов).
Получаем
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




