Введение векторов или координат в планиметрии

Подсказка 1

Пусть R = √2 — длина минутных стрелок, d = 5 — расстояние между центрами крепления стрелок. Как связаны эти 2 величины?

Подсказка 2

Можно заметить, что d > 2R. Часы не пересекаются и их стрелки не пересекаются ни в какой момент времени.

Подсказка 3

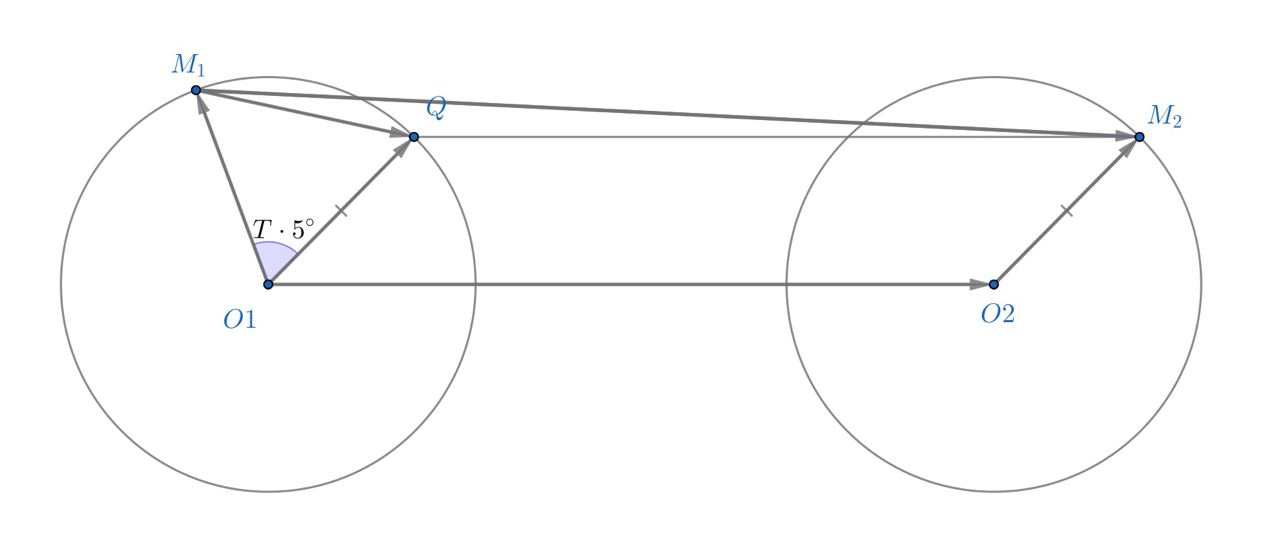
Будем считать вторыми часы, которые идут точно, и первыми — часы, которые отстают от вторых на T = 15 минут. Обозначим как О₁ и О₂ центры первых и вторых часов соответственно, М₁ и М₂ - концы минутных стрелок первых и вторых часов соответственно. Выберем систему координат, в которой ось абсцисс сонаправлена с вектором (O₁O₂). Изобразите часы на картинке и параллельно перенесите вектор (O₂M₂) в точку O₁, получим вектор (О₁Q). Что можно о нем сказать?

Подсказка 4

Можно найти угол между минутными стрелками часов. В задаче просят найти наибольшее и наименьшее расстояние между концами минутных стрелок. Какой это будет вектор?

Подсказка 5

Это (М₁М₂). Выразите его длину через сумму других векторов.

Подсказка 7

(М₁М₂) = (М₁O₁) + (O₁O₂) + (O₂М₂) = ( (М₁O₁) + (O₂М₂) ) + (O₁O₂) = ( (М₁O₁) + (O₁Q) ) + (O₁O₂) = (М₁Q) + (O₁O₂).

Подсказка 8

Найдите (М₁Q), пользуясь теоремой косинусов.

Подсказка 9

(М₁М₂) = (М₁Q) + (O₁O₂), это 2 вектора постоянной длины, при этом угол между ними зависит только от угла между вектором (М₁Q) и положительным направлением оси абсцисс. Этот угол принимает все значения от 0 до 360 градусов, в частности в некоторые два момента времени (М₁Q) сонаправлен и противонаправлен вектору (O₁O₂).

Подсказка 10

Чему равны их длины?

Подсказка 11

Докажите, что длина (O₁O₂) больше длины (М₁Q).

Подсказка 12

Попробуйте применить неравенство треугольника.