Введение векторов или координат в планиметрии

Применяя теорему Менелая к треугольнику и секущим и получаем

Из равенств и следует, что и Подставляя все эти равенства, получаем, что

это означает, что точки и симметричны относительно середины отрезка (см. рис.).

Из условия следует, что лучи и пересекаются в некоторой точке под прямым углом. Тогда в прямоугольном треугольнике медиана равна половине гипотенузы

Обозначим через и середины и соответственно, а через — центр окружности Тогда — точка пересечения серединных перпендикуляров к и которые совпадают с серединными перпендикулярами к и соответственно. Значит, — также центр окружности а — её радиус. Поэтому нам достаточно доказать, что Мы докажем, что — параллелограмм, откуда это и следует.

Поскольку — медиана в треугольнике а — отрезок, соединяющий середины противоположных сторон четырёхугольника имеем

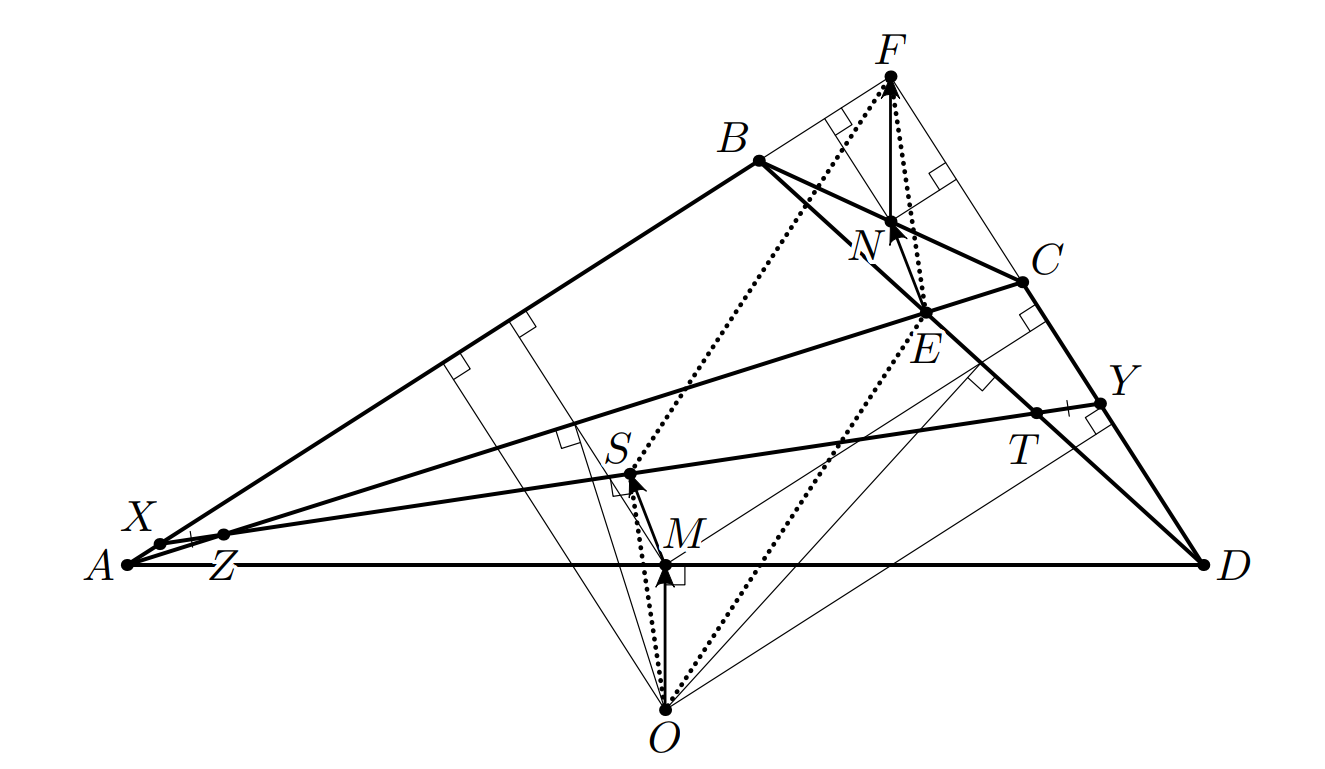
В прямоугольном треугольнике проекции вектора медианы на прямые и равны и соответственно. Поскольку и — центры окружностей и соответственно, при проекции на те же прямые первая попадает в середины отрезков и а вторая — в середины и Поэтому проекции вектора

на эти прямые равны

Значит, проекции векторов и на наши две прямые соответственно равны, откуда

Итак,

откуда и следует, что — параллелограмм.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Есть и другие доказательства того, что — параллелограмм. Например, можно использовать тот факт, что точки и изогонально сопряжены относительно треугольника