.15 Последовательности. Индукция.

Будем доказывать индукцией по количеству прямых.

1. База индукции. При утверждение очевидно. Одна прямая разбивает плоскость на две области, красим одну область в один цвет, другую в другой, и требуемая раскраска получена.

2. Шаг индукции. Пусть наша теорема верна для всевозможных расположений прямых на плоскости. Предположим, что мы провели еще одну, ую прямую. Почему теперь можно покрасить плоскость так, как это требуется в условии задачи? Вообще говоря, даже если по предположению индукции для прямых мы смогли покрасить плоскость нужным нам образом, при случайном проведении -ой прямой, та же самая раскраска может не годиться. Скажем, если при разбиении плоскости прямыми мы покрасили все области вот так

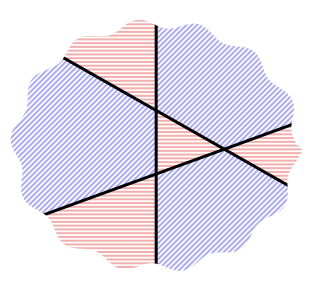
То при проведении новой -ой случайной прямой исходная раскраска уже может не годиться:

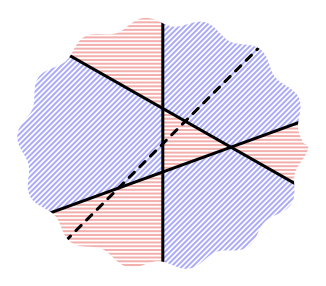
Соседние области здесь уже имеют один и тот же цвет.

Но преобразуем теперь старую раскраску следующим образом: по одну сторону от новой -ой прямой все цвета областей сохраним, а по-другую сторону от нее изменим все цвета областей на противоположные. После такого изменения наша новая раскраска уже заведомо будет подходить под условие задачи.

Действительно, любые две области, не граничащие по -ой прямой либо обе меняют цвет (если находятся по ту сторону от -ой прямой, по которую мы у всех областей сменили цвет), либо обе не меняют цвет.

Но до перекраски они были разноцветными по предположению индукции, значит и останутся таковыми.

А если же две области сейчас стали граничить по -ой прямой, то это значит, что до перекраски они были одного цвета, значит, после нашей перекраски они станут разных цветов.

Следовательно, любые две области с общей границей после этой перекраски будут разноцветными.

Таким образом, если мы верим, что правильная раскраска плоскости существует для любых прямых, то мы можем построить по ней правильную раскраску и для -ой прямой. Что и требовалось доказать.