Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
О треугольнике известно, что длины сторон
и диаметр вписанной окружности являются последовательными членами
арифметической прогрессии. Найдите периметр треугольника, если диаметр вписанной окружности равен 6.
Источники:
Подсказка 1
Не забываем, что диаметр всегда меньше сторон треугольника, так что члены прогрессии можно обозначить за 6, 6 + d, 6 + 2d и 6 + 3d. Нам известен радиус вписанной окружности, мы хотим узнать периметр треугольника, есть ли какие-то формулы, которые связывают эти величины?
Подсказка 2
Есть формула площади S = pr! Но ведь одной формулы недостаточно, надо тогда как-то иначе выразить площадь через d, чтобы мы смогли найти его из полученного уравнения. Какую еще формулу площади можно использовать?
Подсказка 3
Формулу Герона! Теперь у нас есть уравнение, из которого мы сможем найти d, а значит, сможем определить и периметр)
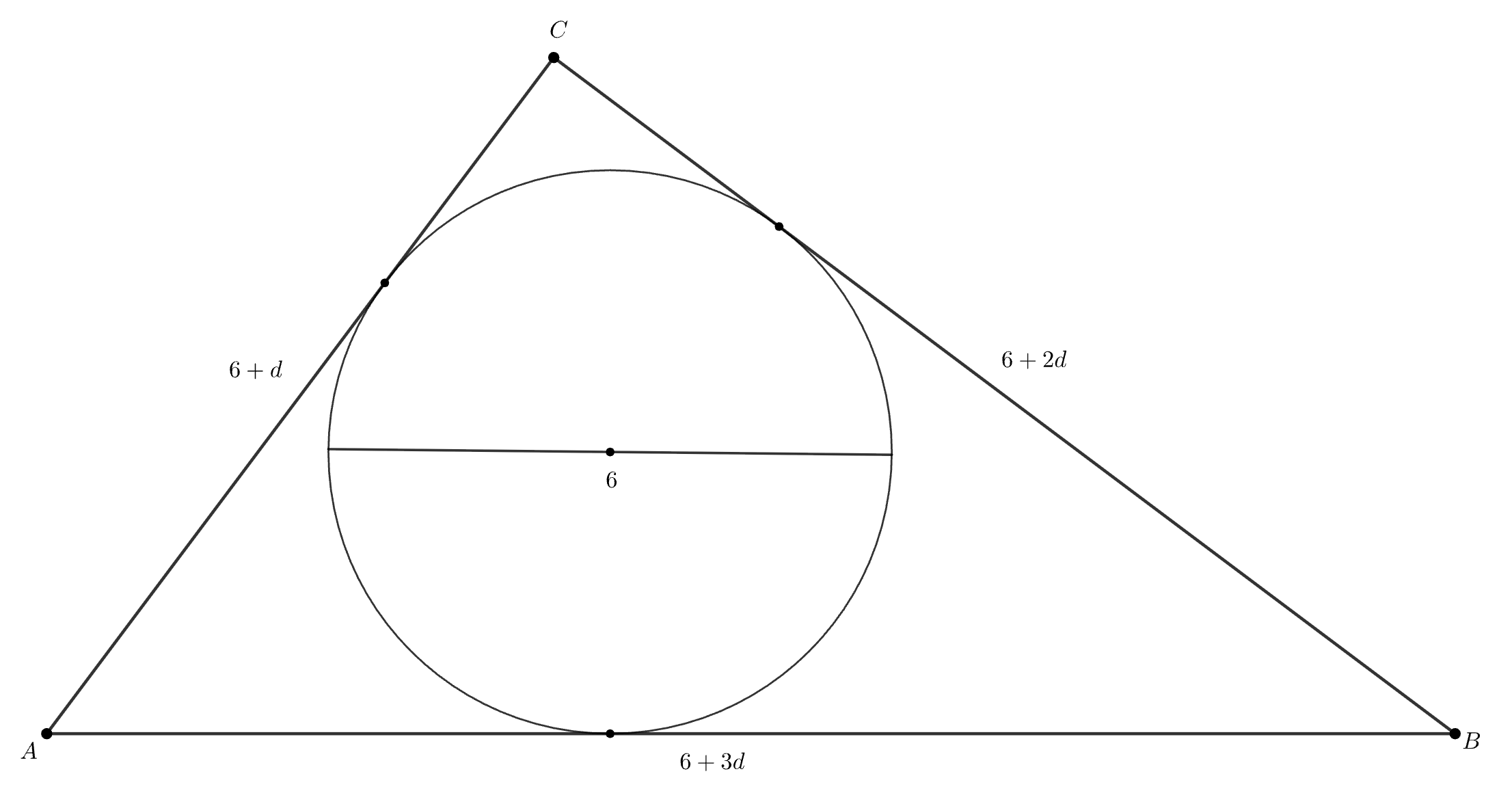
В любом треугольнике диаметр вписанной окружности меньше каждой из сторон треугольника. Пусть
образуют
возрастающую арифметическую прогрессию с разностью
тогда стороны треугольника равны
Тогда полупериметр треугольника равен
Приравняем две формулы для площади треугольника: через радиус вписанной окружности и формулу Герона.
Подставив значения и возведя в квадрат получим,
Так как перепишем левую часть:
Поскольку , то
и мы можем разделить обе части на
Преобразуем:
В итоге периметр треугольника равен
36
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




