Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
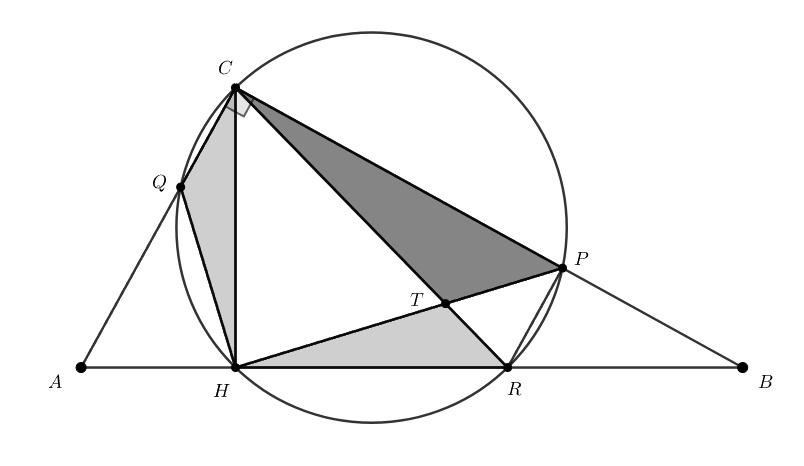
В треугольнике с прямым углом
провели высоту
Окружность, проходящая через точки
и
повторно пересекает
отрезки
и
в точках
и
соответственно. Отрезки
и
пересекаются в точке
Что больше: площадь
треугольника
или сумма площадей треугольников
и
?
Источники:
Подсказка 1
Какие мы знаем стандартные методы для сравнения площадей?
Подсказка 2
Удобно сравнивать площади треугольников с общим основанием, давайте добавим к нашим треугольникам какую-то одинаковую часть.
Подсказка 3
Обратите внимание на треугольник TPR.
Подсказка 4
У нас есть окружность и много прямых углов. На что это намекает?
Подсказка 5
Нетрудно найти на картинке диаметр проведённой окружности. Отметьте прямые углы.
Подсказка 6
Для того, чтобы задача стала совсем простой, нужно провести ещё несколько перпендикуляров. Опустим высоты из точки H на прямые CQ и PR.
Первое решение.
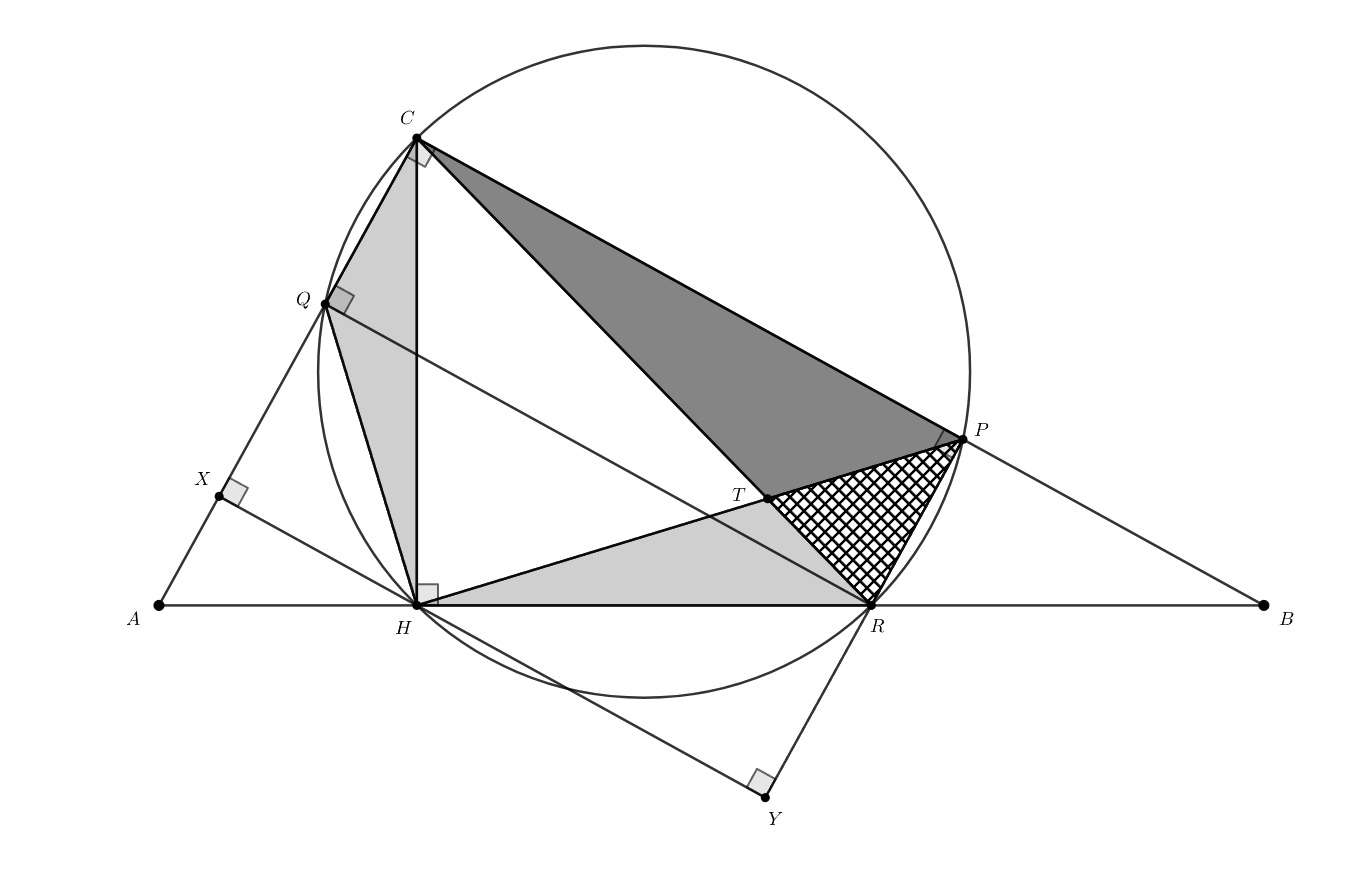
Добавим к рассматриваемым площадям площадь треугольника Получим, что нужно сравнить
Поскольку то
— диаметр проведённой окружности, откуда
В четырёхугольнике
три
угла прямые, поэтому он является прямоугольником. Опустим из точки
перпендикуляры
и
на прямые
и
соответственно. Сумма их длин равна длине стороны
прямоугольника. Следовательно,
___________________________________________________________________________________________________________________________________________________________________
Второе решение.
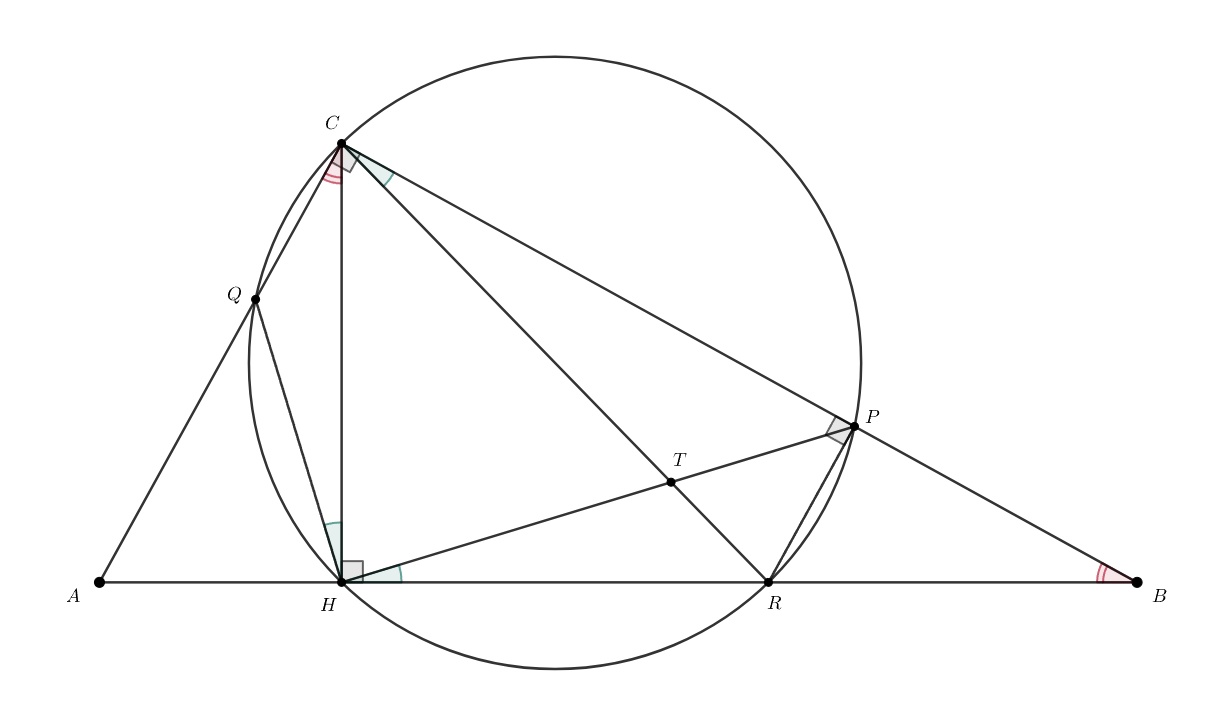
Добавим к рассматриваемым площадям площадь четырёхугольника Получим, что нужно сравнить
Из вписанности следует, что
Поскольку
— диаметр окружности, то
поэтому
Каждый из углов и
дополняет угол
до
поэтому
Следовательно, треугольники
и
подобны по двум углам. Тогда площади этих треугольников относятся как
квадраты коэффициентов подобия, поэтому
Они равны
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




