Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике точка пересечения высот обозначена
Точка
— середина
Через точки
проведена окружность
а через точки
проведена окружность
Прямая
пересекает окружность
в точке
прямая
пересекает окружность
в точке
Прямые
и
пересекают окружности
и
в точках
и
соответственно. Докажите, что
1) точки
лежат на одной прямой;
2) треугольники и
имеют одинаковую площадь.
Источники:
Пункт 1, подсказка 1
Залог успеха любой геометрической задачи — рисунок. Построив рисунок, подумайте, что приблизило бы нас к решению задачи? Может, получится найти какие-то прямые углы?
Пункт 1, подсказка 2
Да, из рисунка похоже, что угол HNS — прямой. Попробуйте подумать, как это можно доказать. Можно ли его выразить через другие углы?
Пункт 1, подсказка 3
Угол HNS можно выразить через углы HSN и SHN. Осталось продолжить цепочку выражений, чтобы упростить задачу. Обратите внимание, какие из углов опираются на одну дугу окружности или являются острыми углами прямоугольного треугольника. Что вы можете сказать об HNR?
Пункт 2, подсказка 1
Обратите внимание на треугольники, которые вместе составляют треугольники ARS и CRS. Может, площади каких-то из них равны?
Проведём высоты треугольника из точек
и
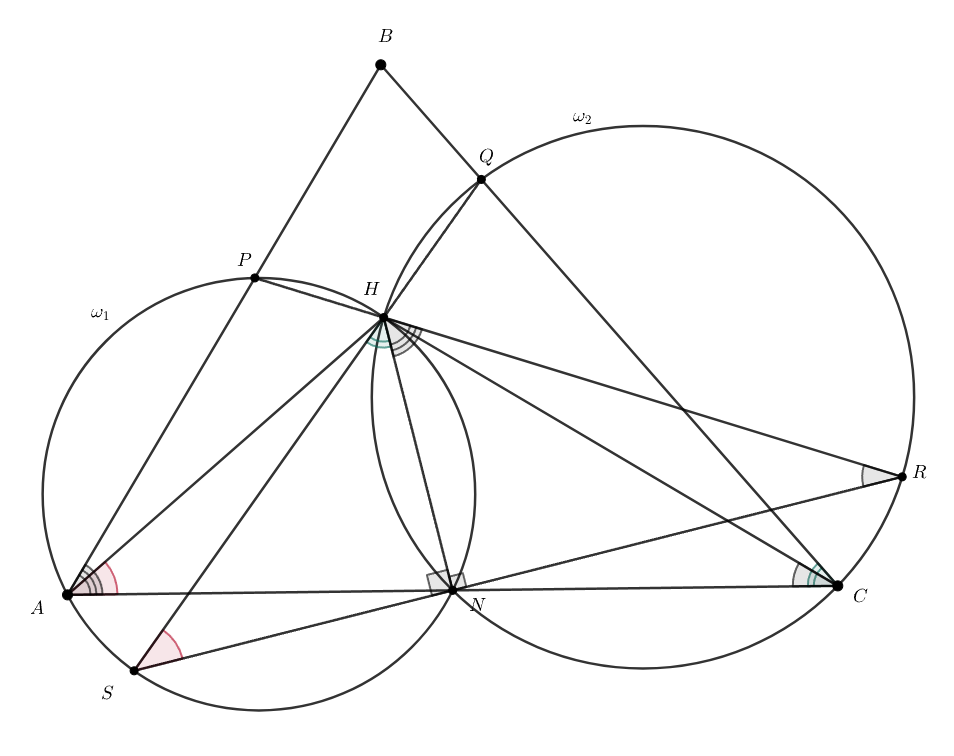
Найдём
Заметим, что как опирающиеся на одну дугу
окружности
Отметим, что так как углы смежные,
то
Итак,
Т.к. по условию
лежат на окружности
то
можно записать как
а
Получаем
Т.к. — острый угол прямоугольного треугольника, то
Но Следовательно,
Аналогично найдём
Итак,
Таким образом, точка принадлежит
2) Заметим, что
Заметим, что
так как в обоих случаях пары треугольников имеют равные высоты и
основания.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




