Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
Внутри прямоугольника выбрана произвольная точка
и проведены отрезки
и
. Площади трёх из
образовавшихся треугольников равны
,
и
(не обязательно в этом порядке). Какие значения может принимать площадь четвёртого
треугольника?
Подсказка 1
Мы знаем площади трёх из четырёх образованных треугольников, можно ли рассматривать какую-то "удобную" пару?
Подсказка 2
Если площади трёх из четырёх треугольников известны, то 2 противолежащие стороны прямоугольника будут принадлежать двум треугольникам с известными площадями!
Подсказка 3
Проведите высоты в треугольниках и выразите с их помощью площадь прямоугольника.
Подсказка 4
Поскольку противоположные стороны прямоугольника равны, можно свести полученное выражение к сумме площадей треугольников. Останется лишь рассмотреть несколько случаев.
Заметим, что нам известны площади треугольников одной из следующих пар: и
и
Рассмотрим первый
случай, второй будет аналогичен.
Опустим перпендикуляры и
на
и
Заметим, что
Рассмотрим возможные величины площади прямоугольника:
1) при
или
тогда площадь четвертого треугольника равна
Это возможно, если точка
лежит на стороне прямоугольника.
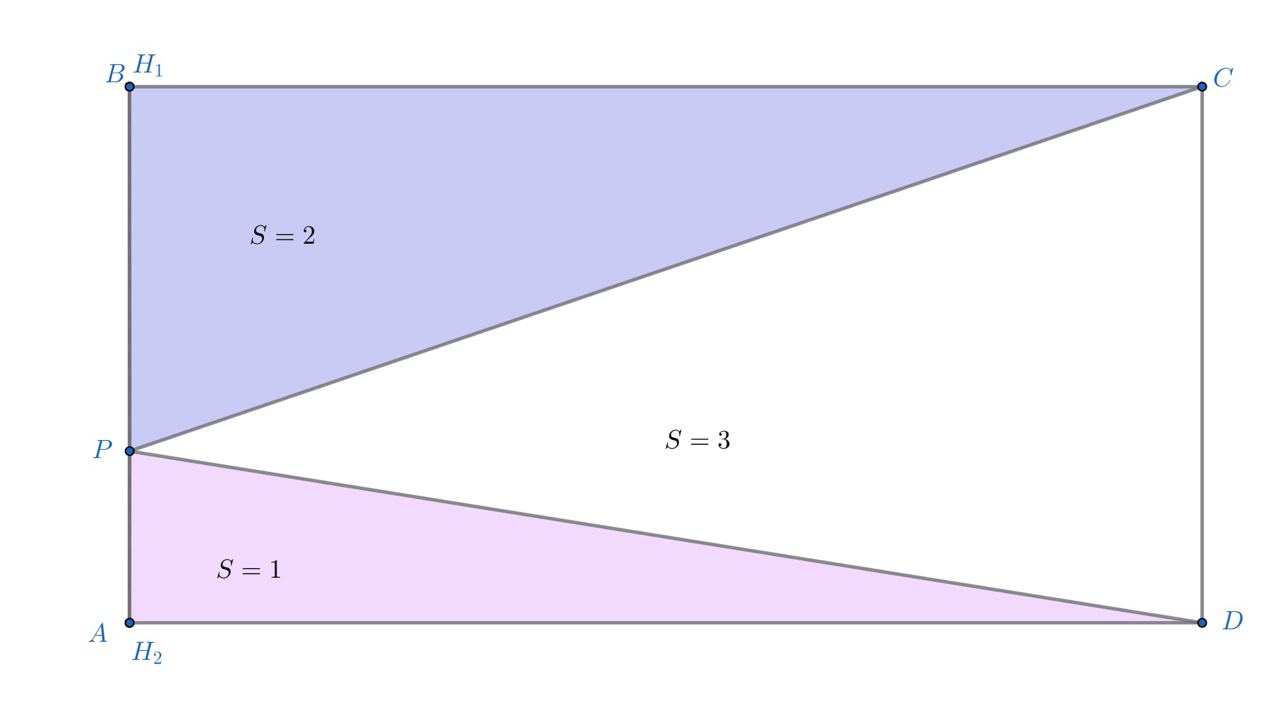
2) при
или
тогда площадь четвертого треугольника равна
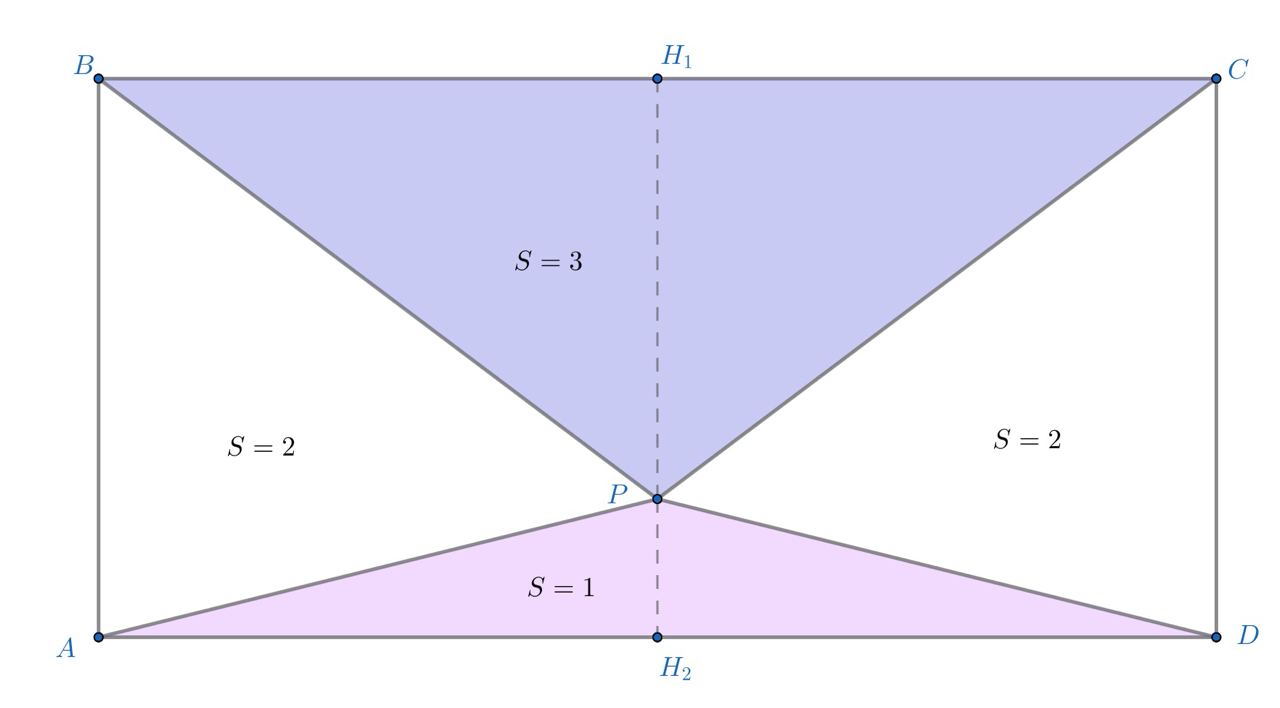
3) при
или
тогда площадь четвертого треугольника равна
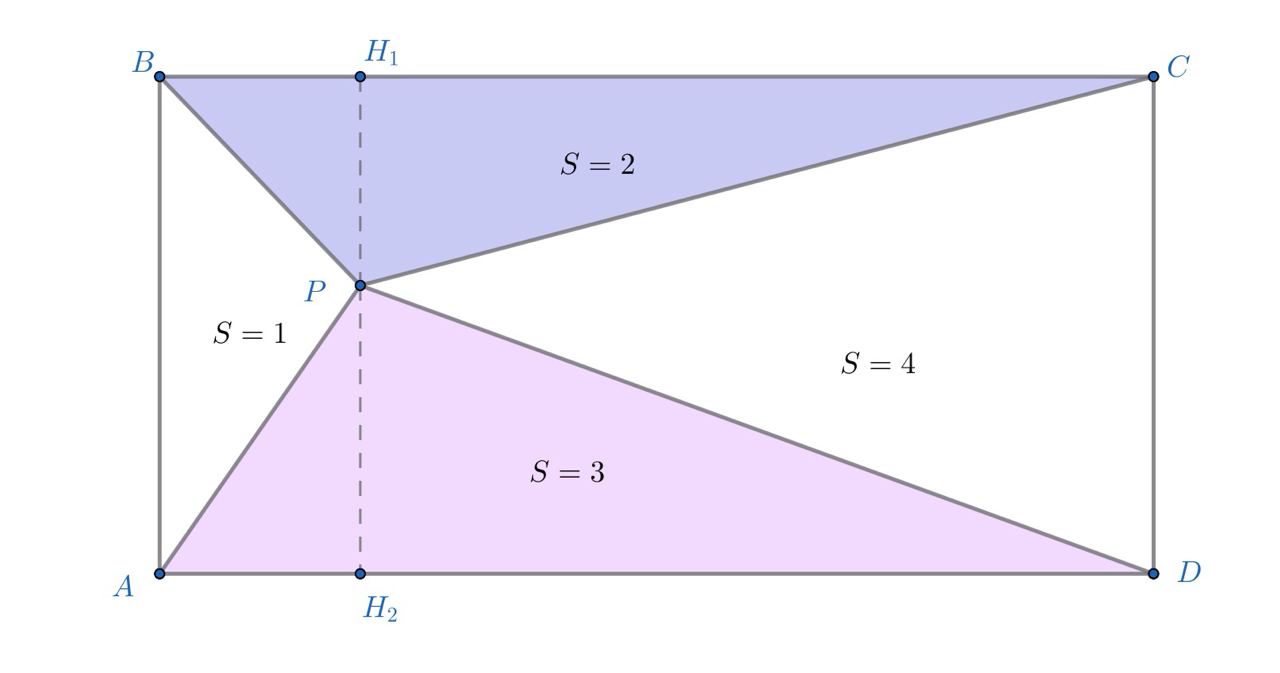
Замечание. В каждой случае приведен рисунок одной конфигурации из двух возможных.
0, 2, 4
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




