Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
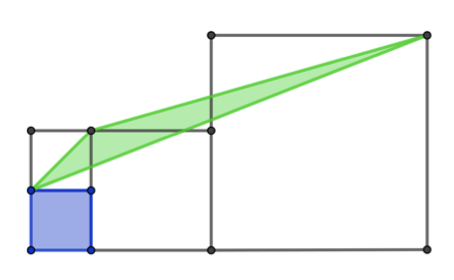
Четыре квадрата расположены как на рисунке справа. Площадь закрашенного квадрата равна 7. Чему равна площадь закрашенного треугольника?
Подсказка 1
Нам дана только площадь синего квадрата. Можно ли получить еще какие-то данные с картинки?
Подсказка 2
Нет ли на картинке равных фигур?
Подсказка 3
Да, 2 малых квадрата будут равными, следовательно, их площади равны. А что можно сказать про средний квадрат?
Подсказка 4
Заметьте, что стороны малых квадратов вместе дают сторону среднего квадрата.
Подсказка 5
Тогда сторона среднего квадрата в 2 раза больше стороны малого квадрата. Выразите площадь среднего квадрата.
Подсказка 6
Пусть сторона меньшего квадрата равна x, тогда сторона среднего — 2x. Заметим, что площадь малого квадрата равна x², а площадь среднего — 4x². Более того, мы знаем, чему равно x².
Подсказка 7
Кажется, все, что можно найти на исходной картинке, мы нашли, но до сих пор не приблизились к площади зеленого треугольника, уж слишком странной он формы. Надо ли вообще искать именно его площадь?
Подсказка 8
А что, если попробовать найти фигуру, площадь которой будет равна площади зеленого треугольника?
Подсказка 9
Из какой конструкции можно получить 2 равновеликих треугольника?
Подсказка 10
Нам могут помочь рельсы Евклида, надо лишь их увидеть. А как именно образуются рельсы Евклида?
Подсказка 11
Основание для треугольников берется на некоторой прямой A, а вершины треугольников — на прямой B, параллельной A! Какой прямой может быть параллельна сторона зеленого треугольника, являющаяся диагональю малого квадрата?
Подсказка 12
Может, вторая прямая — тоже диагональ?
Подсказка 13
Рассмотрите диагональ наибольшего квадрата.
Подсказка 14
Осталось только посчитать площадь нового треугольника. В какой фигуре он находится?
Подсказка 15
На самом деле, это прямоугольник. Можно поступить следующим образом: сначала найдем площадь прямоугольника, а потом вычтем из нее площади треугольников, которые дополняют искомый треугольник до прямоугольника! Давайте назовем в прямоугольнике все отмеченные на рисунке точки, идя слева-направо сверху-вниз, следующими буквами: A, B, C, D, E, F, G, H. Чему будет равна площадь треугольника ADB?
Подсказка 16
Он же составляет половину малого квадрата! Значит, и площадь его в 2 раза меньше.
Подсказка 17
С треугольником BCH все аналогично, осталось лишь разобраться с DFH. Можно ли тоже представить его как часть другой фигуры?
Подсказка 18
А попробуйте провести через точку D прямую, параллельную FG, пусть она пересечет отрезок CH в точке E'. Что можно сказать о четырехугольнике FDE'H?
Подсказка 19
Да это же прямоугольник! Какую часть от него будет составлять DFH? А какую часть от FACH составит FDE'H?
Введём обозначения как показано на рисунке ниже.
Так как
то
Аналогично,
Получим, что в квадратах
и
параллельны
следующие стороны:
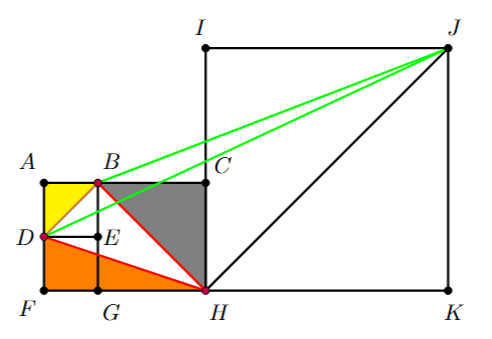
Тогда диагонали и
будут параллельны. Рассмотрим треугольник
Так как точки
и
лежат на
прямой, параллельной
треугольники
и
будут равновеликими. Далее будем искать площадь треугольника
Так как и
равны,
получаем, что квадраты
и
подобны с коэффициентом
тогда
Кроме того,
Чтобы найти площадь треугольника надо отнять от площади прямоугольника
площади треугольников
и
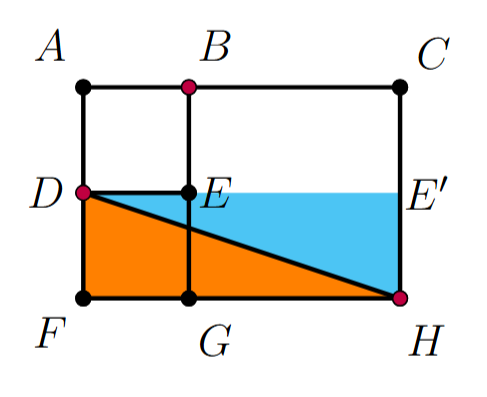
Проведем параллельно
тогда
Прямоугольники
и
равны, так как
Они образуют
прямоугольник
следовательно,
Заметим, что треугольники и
равны, так как являются прямоугольными,
и
— общая сторона.
Следовательно,
Тогда площадь искомого треугольника равна
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




