Счёт площадей, рельсы Евклида, теорема о линолеуме

В точке пересекаются три высоты треугольника. Так как — центр описанной окружности, то в точке пересекаются серединные перпендикуляры треугольника. Так как точка — середина стороны то — медиана. Точка — точка пересечения медианы и прямой

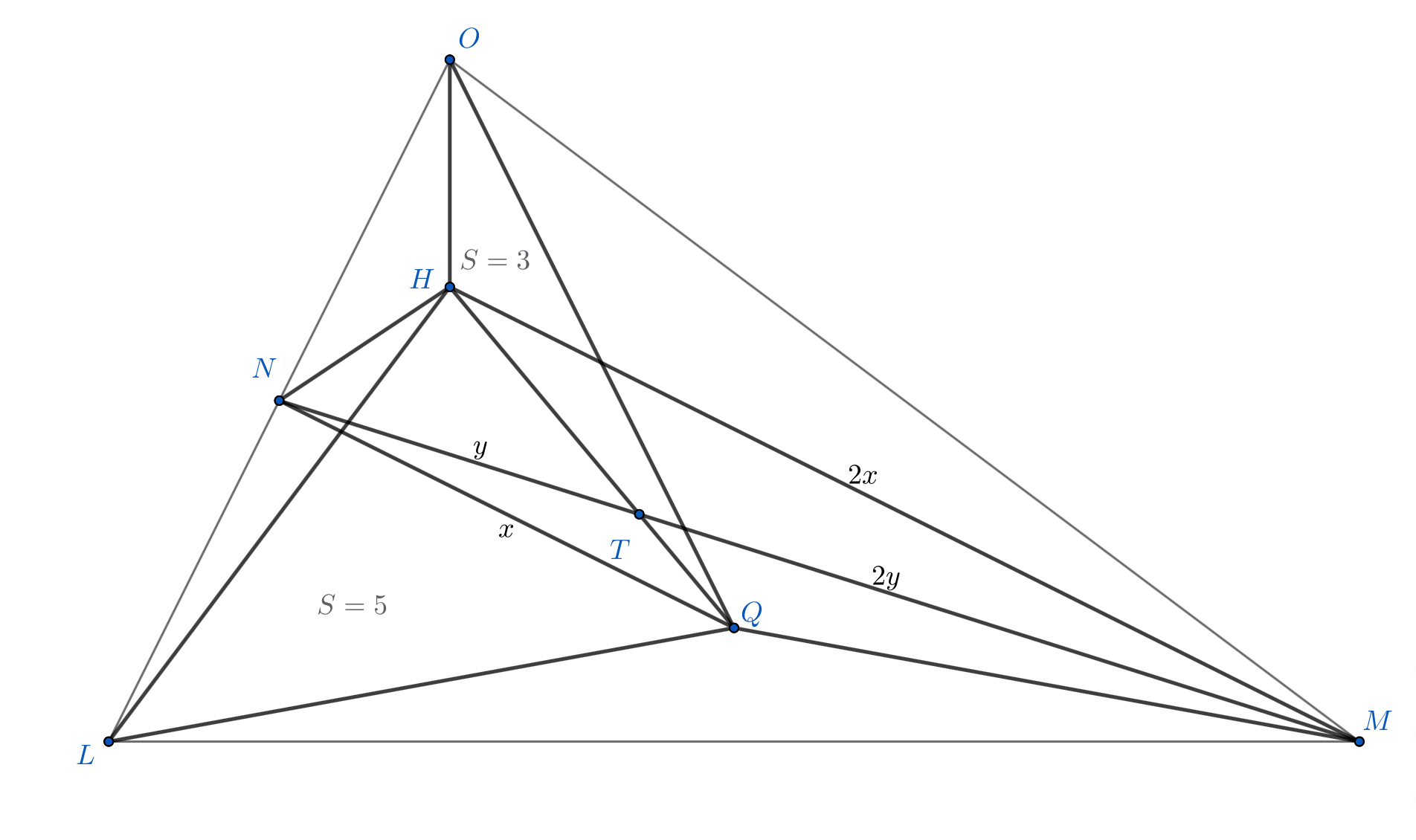
Треугольники и подобны — это следует из параллельности прямых и которые обе перпендикулярны прямой . По теореме о прямой Эйлера , тогда коэффициент подобия равен 2.

Значит, то есть медиана делится точкой в отношении Это означает, что — точка пересечения медиан треугольника

Поэтому площадь в 2 раза больше площади Так как — середина то

Рассмотрим несколько случаев, чтобы определить, какая из площадей является суммой двух других. Для этого нам важно понять, где прямая пересекает стороны треугольника.

Если треугольник правильный, то точки и совпадают и указанные в условии задачи три площади вырождаются. Это здесь невозможно, так как дано, что площади равны 3 и 5.

Если прямая проходит через любую вершину треугольника, то тогда одна из трех площадей равна 0, а две другие — ненулевые, но равны между собой — этот случай нам не подходит.

Если же прямая пересекает две стороны (рассмотренный выше случай), то мы доказали, что одна из этих трех площадей (в первом случае это во втором — в третьем — ) является суммой двух других.

Поэтому получаем либо либо либо что невозможно.