Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
В треугольнике выбрана точка
так, что
Прямая
пересекает
в точке
Докажите, что
— середина
Подсказка 1
В этой задаче нам не даны никакие углы и отрезки, то есть по сути мы можем воспользоваться только площадями, их отношениями и отношениями отрезков.
Подсказка 2
Площади двух треугольников, на которые делится больший треугольник одной чевианой, относятся так же, как как и их основания, лежащие на той стороне, к которой проведена чевиана!
Подсказка 3
Предположим, что M — середина BK. Что тогда можно было бы сказать про площади некоторых треугольников?
Подсказка 4
Площади треугольников △BMA и △MAK были бы равны!
Подсказка 5
Обозначим площадь треугольника △MAK как S и выпишем отношения отрезков ВМ/МК через площади, отсюда несложно найти S!
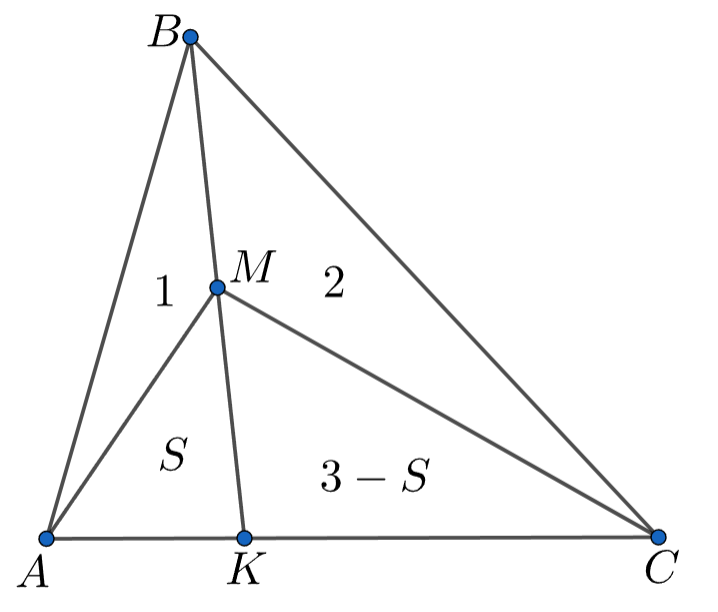
Обозначим площадь треугольника через
тогда площадь треугольника
равна
С одной стороны,
а с другой стороны
Отсюда получаем уравнение
которое имеет решение
Теперь видно, что
делит треугольник
на два равновеликих, а значит, является его медианой. Получили
требуемое.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




