Счёт площадей, рельсы Евклида, теорема о линолеуме
Ошибка.
Попробуйте повторить позже
Внутри стороны выпуклого четырехугольника
нашлась такая точка
что прямая
делит четырёхугольник на две
равные по площади части. Какая из вершин четырехугольника находится дальше всех от прямой
Подсказка 1
Опустим из точек B, C, D перпендикуляры BB₁, CC₁, DD₁ на AE. В самом деле расстояние от A до AC равно нулю, потому нас интересует максимум из трёх проведённых перпендикуляров. У нас есть условие на равенство площадей треугольника ABE и четырёхугольника ADCE. Как отсюда сравнить отрезки BB₁, CC₁, DD₁?
Подсказка 2
Домножив длины отрезков на AE/2, получим площади треугольников ABE, ACE, ADE. Осталось их сравнить.
Подсказка 3
Площади треугольников ACE и ADE строго меньше площади четырёхугольника ADCE (ведь он является выпуклым). А значит, максимум из трёх площадей — площадь треугольника ABC, а максимум из трёх перпендикуляров — BB₁.
Опустим перпендикуляры на прямую
откуда Аналогично из неравенства
получаем, что
Поскольку расстояние от точки
до прямой
равно
получаем, что вершина
удалена от прямой
больше, чем все остальные вершины четырехугольника
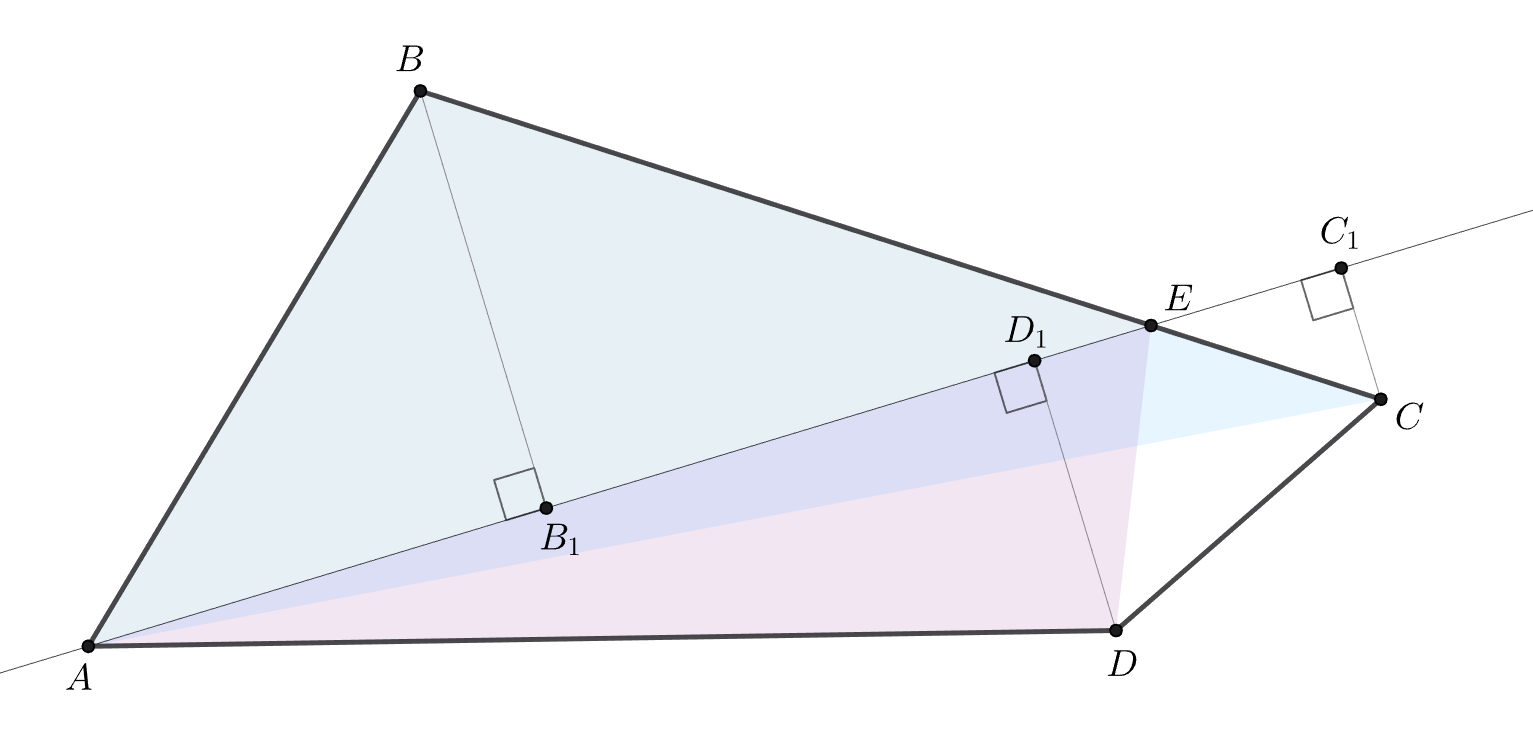
Вершина
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




