Описанная сфера

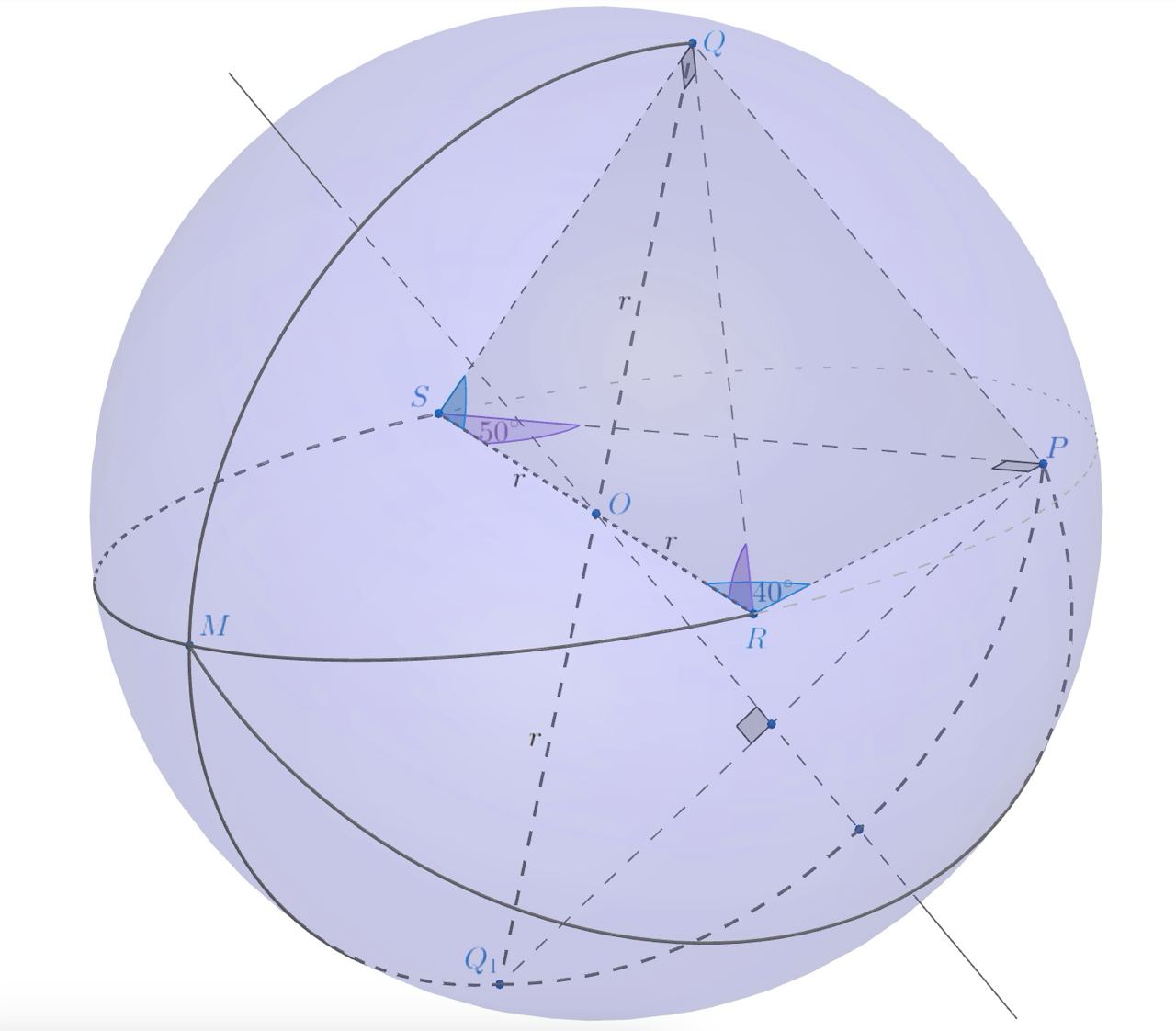
Так как

то треугольники и — прямоугольные с общей гипотенузой . Если — середина отрезка , то по свойству медианы прямоугольного треугольника . Следовательно, радиус описанной сферы равен 3, а точка — её центр.

Обозначим через сферическое расстояние между точками и . По условию задачи необходимо найти площадь множества на сфере, состоящего в точности из точек , для которых

Поскольку — диаметр сферы, то точки и лежат на одной окружности большого круга; следовательно,

Неравенство (1) перепишется в виде

Пусть — точка, симметричная точке относительно центра сферы . Так как и — концы диаметра сферы, то

Подставляя в неравенство (2), получаем

Так как , то не является диаметром, а потому . Итак, есть множество точек на сфере, сферическое расстояние от которых до одной точки на сфере не превосходит сферического расстояни до другой точки на сфере. В силу симметрии (относительно плоскости, проходящей через центр сферы перпендикулярно отрезку , — половина сферы и её площадь равна