Описанная сфера

Плоскости оснований и призмы пересекают сферу по окружностям, описанным около правильных треугольников и пусть их центры — точки и соответственно.

Легко показать, что середина отрезка является центром сферы.

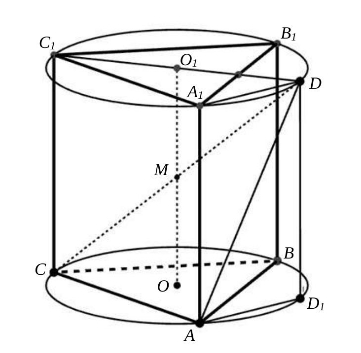
Проведем через точку диаметр окружности с центром в точке Покажем, что — диаметр сферы. Действительно, плоскость перпендикулярна плоскостям основания и, значит, вместе с точкой содержит отрезок Т.к. прямая пересекает отрезок в его середине, т.е. в центре заданной сферы.

Пусть — проекция точки на плоскость основания высота призмы равна а радиусы окружностей с центрами и равны Рассмотрим треугольники и Учитывая, что (треугольник равносторонний), по т. Пифагора получаем систему уравнений:

Решая систему, находим, что Тогда сторона основания равна его площадь и следовательно, объем призмы