Описанная сфера
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде с вершиной
и основанием
дана высота
и
Найти радиус сферы,
описанной около пирамиды.
Пусть точка — основание высоты пирамиды, точка
— центр описанной окружности сферы,
— радиус этой сферы. Тогда
По свойству правильной пирамиды точка
лежит на прямой
являющейся высотой.
Рассмотрим треугольник Он прямоугольный, так как
перпендикулярна плоскости
то есть перпендикулярна и
прямой
лежащей в
как радиус окружности, описанной около правильного треугольника со стороной
Рассмотрим, чему может быть равна длина отрезка
в зависимости от положения точки
относительно точек
и
- 1.
-
Пусть
лежит на отрезке
Тогда

- 2.
-
Пусть
лежит за точкой
то есть точки
и
находятся по разные стороны от точки
Тогда

- 3.
-
Пусть
лежит за точкой
то есть точки
и
находятся по разные стороны от точки
Но тогда
и в прямоугольном треугольнике
катет
больше чем гипотенуза
что не возможно, то есть
не может лежать за
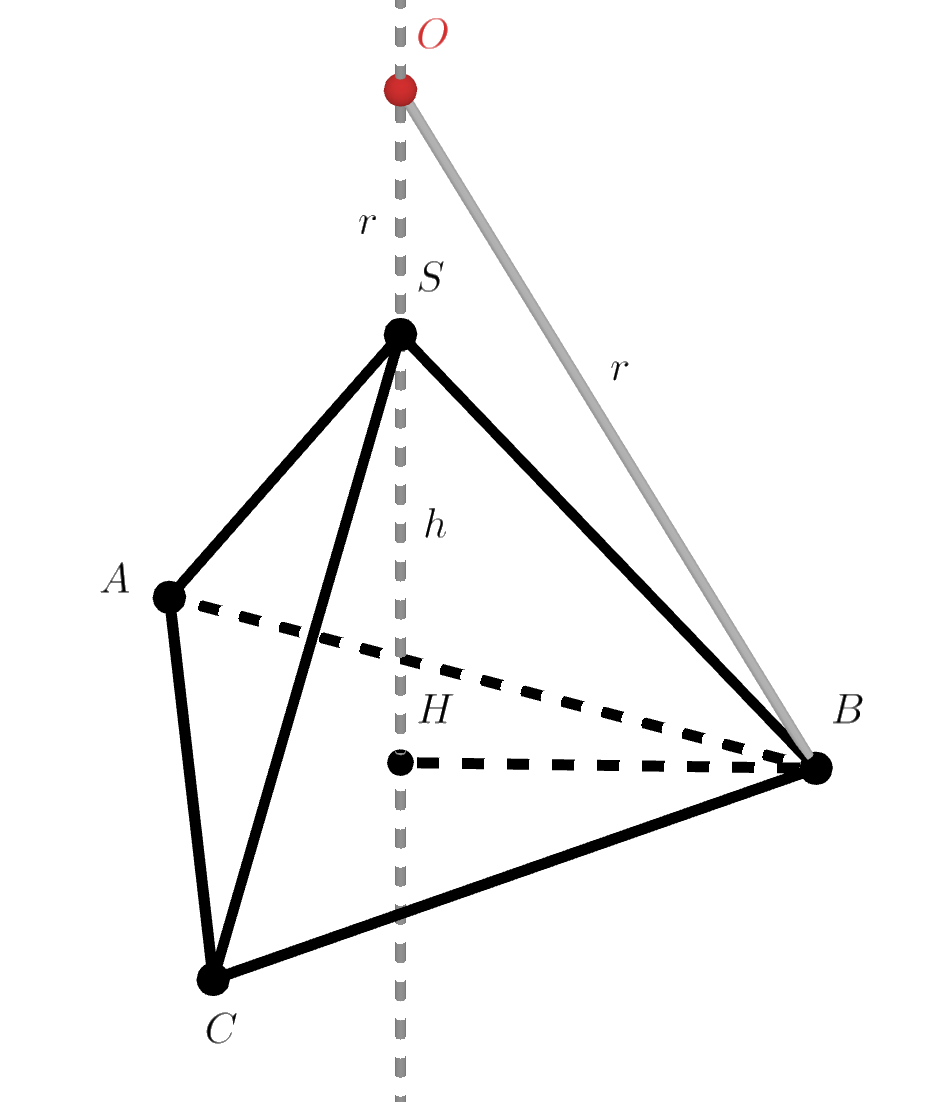
Получается, что По теореме Пифагора:
Ошибка.
Попробуйте повторить позже
Основанием пирамиды служит треугольник со сторонами
Все боковые рёбра равны
Найдите радиус сферы, описанной
около пирамиды.
Пусть — треугольник, который служит основанием пирамиды, при этом
Заметим, что
то
есть
откуда
— прямоугольный треугольник с гипотенузой
Все рёбра пирамиды равны, а значит, точки и
равноудалены от четвёртой вершины пирамиды. Геометрическое место точек,
равноудалённых от
и
— прямая, перпендикулярная плоскости
и проходящая через центр окружности, описанной около
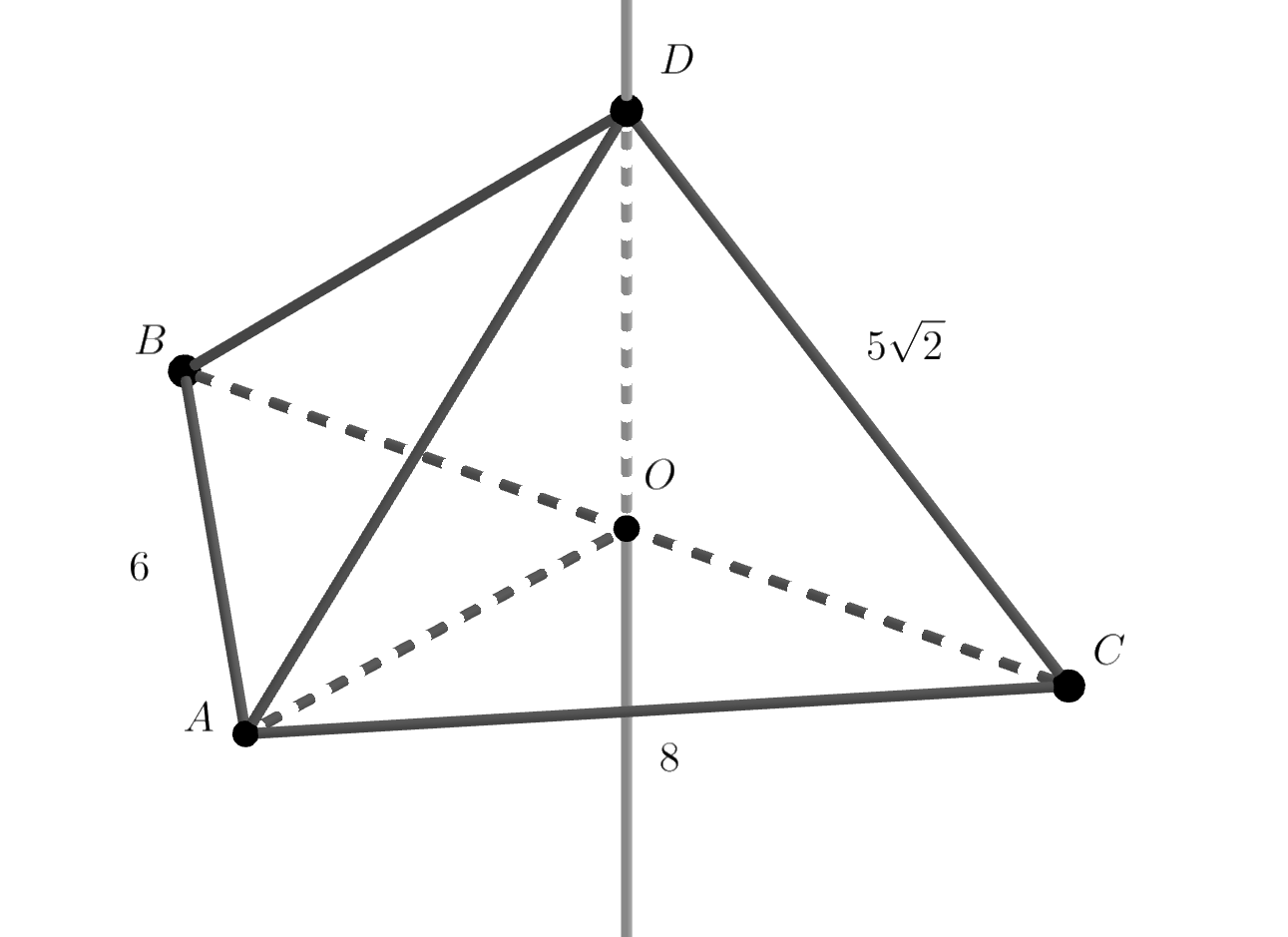
Так как треугольник — прямоугольный, то центр его описанной окружности лежит на середине его гипотенузы. Пусть точка
—
середина
тогда вершина пирамиды
лежит на прямой, перпендикулярной плоскости
и проходящей через точку
а так
же
Треугольник — прямоугольный, так как прямая
перпендикулярна плоскости
то есть перпендикулярна и прямой
лежащей в
как ребро пирамиды,
отсюда
Получается, то есть точка
равноудалена от всех вершин пирамиды, откуда точка
— центр описанной
сферы. Значит, радиус описанной сферы равен 5.
5
Ошибка.
Попробуйте повторить позже
Основание высоты
треугольной пирамиды
принадлежит грани
Найти радиус сферы, описанной около пирамиды
Подсказка 1
Давайте обозначим центр нашей сферы за O. Разумно будет опустить перпендикуляры OO₁ и OO₂ на плоскости (ABC) и (ASB) соответственно. Что тогда можно сказать про точки O₁ и O₂?
Подсказка 2
Правильно, это центры описанных окружностей треугольников △ABC и △ASB. Т.к. ∠AO₁B- центральный, то ∠AO₁B=2∠ACB=120°. Заметим, что △ASB- тупоугольный, а это значит, что O₂ лежит вне треугольника △ASB ⇒ ∠AO₂B=120°. Тогда равнобедренные треугольники △AO₂B и△ AO₁B равны. А что можно сказать про треугольники △OO₂M и △OO₁M, где M- середина AB?
Подсказка 3
Они равны! Т.к. OM, O₁M, O₂M ⊥ AB ⇒ O, O₁, O₂, M лежат в одной плоскости. Вот если бы мы знали уголок ∠O₂MO₁, мы бы легко нашли OO₁... Погодите, ведь ∠O₂MO₁ это просто больший из линейных углов двугранного угла между плоскостями (ABC) и (ASB)...
Подсказка 4
Итак, раз уж вы нашли этот уголок, то ∠OMO₁=∠O₂MO₁/2 ⇒ можем вычислить OO₁. Осталось лишь написать теорему Пифагора для треугольника △OBO₁ и найти OB=R!
![]()
По теореме косинусов из треугольника находим, что
Пусть - высота треугольника
. Тогда
С другой стороны,
Из уравнения находим, что
По теореме о трёх перпендикулярах
поэтому
- линейный угол
двугранного угла между плоскостями граней
и
Обозначим
Из прямоугольного треугольника
находим,
что
Тогда
![]()
Пусть и
- проекции центра
сферы, описанной около пирамиды
на плоскости граней
и
соответственно.
Тогда
и
- центры описанных окружностей треугольников
и
Тогда, если
- середина ребра
то
и
Поскольку центр
описанной окружности треугольника
и вершина
лежат по разные стороны от
прямой
значит, центр
сферы лежит внутри тупого двугранного угла, образованного плоскостями граней
и
Рассмотрим сечение пирамиды плоскостью, проходящей через прямые и
Прямая
перпендикулярна этой плоскости, т.к.
она перпендикулярна
то точка
также принадлежит этой плоскости. Заметим, что
поскольку центральный угол вдвое больше соответствующего вписанного. Из равнобедренных треугольников и
находим, что
Прямоугольные треугольники и
равны по гипотенузе и катету, поэтому
а т.к.
то
Тогда
Пусть искомый радиус описанной сферы пирамиды
Из прямоугольного треугольника
находим,
что
Ошибка.
Попробуйте повторить позже
Десять шаров одинакового радиуса сложены в виде треугольной пирамиды так, что каждый шар касается как минимум трёх других. Найти
радиус сферы, в которую вписана пирамида из шаров, если радиус шара, вписанного в центр пирамиды из шаров, касающегося шести
одинаковых шаров, равен
Источники:
При таком расположении десяти одинаковых шаров центры четырёх из них расположены в вершинах правильного тетраэдра, а
точки касания расположены на ребрах этого тетраэдра. Следовательно, ребро тетраэдра равно четырём радиусам этих шаров, радиус
внешней сферы больше радиуса шара, описанного около тетраэдра на четверть длины ребра тетраэдра, а радиус внутреннего
шара меньше расстояния от центра тетраэдра до его грани на эту же величину. Рассмотрим сечение тетраэдра плоскостью
:
Обозначим длину ребра тетраэдра за , радиус сферы, описанной вокруг пирамиды из шаров за
, радиус шара, вписанного в центр
пирамиды из шаров за
.
В треугольнике
следовательно,
Из подобия треугольников и
имеем
В треугольнике :
следовательно,
Тогда
Таким образом,
откуда
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида. Известно, что центр сферы, описанной около этой пирамиды, равноудалён от боковых рёбер и от
плоскости основания пирамиды. Найдите радиус сферы, вписанной в эту пирамиду, если длина ребра её основания равна
Подсказка 1
Назовём нашу пирамиду SABC, где △ABC будет основанием. Попытаемся узнать длину бокового ребра, пользуясь данными о том, что центр описанной около этой пирамиды сферы равноудалён от боковых рёбер и плоскости основания. Где относительно высоты пирамиды будет расположен центр описанной сферы? Пусть Н — основание высоты, а О₁ — центр описанной сферы. Что можно сказать про △ASH, пользуясь тем, что точка О равноудалена от точки Н и прямой AS, а также от точек S и A?
Подсказка 2
Пирамида правильная, значит мы точно знаем положение точки Н, длину АН и отсюда сможем вытащить AS. Теперь мы знаем длины всех рёбер пирамиды! Подумайте, как можно вытащить радиус вписанной сферы?
Подсказка 3
Центр вписанной сферы О₂ также лежит на высоте пирамиды. Нетрудно доказать, что если М — середина АВ, то именно в плоскости (MSH) будут лежать радиусы, проведённые в точки касания сферы с гранями АВС и SAB. Рассмотрите △MSH, как мы можем в нём посчитать O₂H?
Подсказка 4
MH нетрудно ищется из свойств правильного треугольника. Пифагор поможет нам найти SM и SH. О₂, как точка равноудалённая от сторон МН и MS лежит на биссектрисе угла M. Осталось только применить свойство биссектрисы и задача решена!
Пусть — основание пирамиды,
— вершина,
— центр треугольника
— середина
— центр описанной сферы,
— центр вписанной сферы. Поскольку точка
равноудалена от
и
— биссектриса треугольника
Стало быть,
![]()
Поскольку имеем
откуда
Для треугольника
имеем
откуда
Поскольку
— биссектриса,
Стало быть,
откуда
Ошибка.
Попробуйте повторить позже
В сферу радиуса вписана правильная треугольная призма
с основанием
и боковыми ребрами
Отрезок
— диаметр этой сферы. Найти объем призмы, если
Источники:
Подсказка 1
Нам нужно понять, от чего зависит конструкция, то есть какими параметрами задаётся. С учетом того, что нам надо найти объём, то есть найти площадь основания на высоту, какие параметры нам удобно ввести, чтобы через них всё выражалось?
Подсказка 2
Удобно ввести высоту и радиус окружностей, в которые вписано каждое из оснований. Тогда, поскольку в силу симметрии CD — диаметр, то нам известна длина CD, а также известна длина AD. Это значит, что у нас есть два уравнения на две переменных (r и h), поскольку есть два прямоугольных треугольника у которого стороны либо константы, либо выражаются через r и h. Осталось решить такую систему и посчитать объём!
Плоскости оснований и
призмы пересекают сферу по окружностям, описанным около правильных треугольников
и
пусть их центры — точки
и
соответственно.
Легко показать, что середина отрезка
является центром сферы.
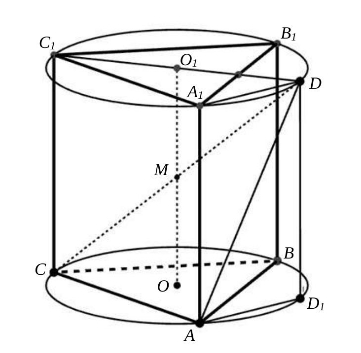
Проведем через точку диаметр
окружности с центром в точке
Покажем, что
— диаметр сферы. Действительно,
плоскость
перпендикулярна плоскостям основания и, значит, вместе с точкой
содержит отрезок
Т.к.
прямая
пересекает отрезок
в его середине, т.е. в центре
заданной сферы.
Пусть — проекция точки
на плоскость основания
высота призмы равна
а радиусы окружностей с центрами
и
равны
Рассмотрим треугольники
и
Учитывая, что
(треугольник
равносторонний),
по т. Пифагора получаем систему уравнений:
Решая систему, находим, что Тогда сторона основания равна
его площадь
и следовательно, объем
призмы
Ошибка.
Попробуйте повторить позже
Дан тетраэдр . Известно, что центр сферы, описанной около этого тетраэдра, лежит на
, что плоскости
и
перпендикулярны и что
. Найдите угол между прямыми
и
Источники:
Подсказка 1
Пусть К — центр описанной сферы. Отметьте равные отрезки-радиусы сферы. Какой вывод можно сделать, смотря на △ADB и его медиану, равную половине стороны? Какой вывод можно сделать о △АВС?
Подсказка 2
Итак, перед нами два прямоугольных треугольника с общей гипотенузой и равными катетами, значит они сами...? Проведите высоту DH в △ADB, что можно сказать об отрезке СН, пользуясь перпендикулярностью плоскостей?
Подсказка 3
Из равенства треугольников можно вывести, что ВН = АН, то есть Н совпадает с К, значит △ADB и △AСB не только прямоугольные, но и...?
Подсказка 4
Отметьте L и M — середины рёбер BD и CD соответственно. Что можно сказать о связи LM и BC? А о LK и AD? Осталось внимательно рассмотреть △MLK и записать ответ!
Сразу отметим, что, поскольку центр сферы, описанной около тетраэдра, лежит на , углы
и
- прямые. Далее, опустим
перпендикуляры
и
на
и
соответственно. Тогда
, ибо
, следовательно,
серединный
перпендикуляр к
в плоскости
и, поскольку
, точка
является серединой
. Значит,
. Аналогично,
Итак, . Пусть
точка, симметричная точке
относительно
. Тогда
и
. Следовательно, треугольник
равносторонний. При этом
.
Стало быть, искомый угол равен углу
и равен
Ошибка.
Попробуйте повторить позже
Дан параллелепипед с основаниями
и боковыми рёбрами
. Все рёбра
параллелепипеда равны. Плоские углы при вершине
также равны. Известно, что центр сферы, описанной около тетраэдра
,
лежит в плоскости
. Радиус этой сферы равен 2. Найдите длину ребра параллелепипеда.
Источники:
Подсказка 1
В вершине В сходятся 3 равных угла, что можно сказать об отрезках-диагоналях граней, лежащих напротив этой вершины? (Строго обосновать этот факт можно через треугольники, равные по 2-м сторонам и углу между ними!)
Подсказка 2
В какой ещё из вершин параллелепипеда сходятся 3 равных угла? Какой вывод можно сделать об отрезках-диагоналях граней, исходящих из этой же вершины?
Подсказка 3
Каким свойством в таком случае обладает тетраэдр D'AB'C: у него равны боковые рёбра и в основании лежит правильный треугольник? Таким образом мы можем вычислить все его стороны!
Подсказка 4
Восстановите длину стороны ромбов-граней по найденным диагоналям и можно записывать ответ!
Грани параллелепипеда являются ромбами. Поскольку плоские углы при вершине равны, равны также и плоские углы при вершине
. Стало быть,
как равные диагонали ромбов и, по той же причине,
. Таким образом, центр
сферы, описанной около тетраэдра
, является центром окружности, описанной около правильного треугольника
, а также
является основанием высоты тетраэдра, опущенной из вершины
. Отсюда получаем
. Итак, диагонали ромба
равны
и
, значит, его сторона равна
Ошибка.
Попробуйте повторить позже
Дана усечённая пирамида с боковыми рёбрами
,
,
, такая, что треугольник
— равносторонний. На ребре
, перпендикулярном основанию
пирамиды, лежит точка
такая, что
Сфера
с радиусом
проходит через вершины треугольника
и касается отрезка
в точке
.
(b) Пусть дополнительно известно, что . Найдите угол между прямой
и плоскостью
, а также
длину ребра
Пункт а), подсказка 1
Введем обозначения: пусть E – вершина пирамиды, O – центр сферы ω, O₁ – центр описанной окружности треугольника BB₁C, а F – середина BC. Если треугольник BB₁C равносторонний, то чем еще будет являться точка O₁? А какие прямые будут проходить через нее?
Пункт а), подсказка 2
Верно, O₁ будет также точкой пересечения медиан, значит через нее пройдет прямая B₁F, Вы даже можете спокойно найти, в каком отношении точка O₁ поделит отрезок B₁F. А что тогда можно будет сказать про взаимное расположение прямой NO₁ и плоскости (ABC)?
Пункт а), подсказка 3
Конечно, прямая NO₁ будет параллельна плоскости (ABC). А теперь поработаем с нашей сферой! Из условия сфера касается AA₁ в точке N, а также проходит через вершины треугольника BB₁C, чему тогда будут перпендикулярны прямые OO₁ и ON?
Пункт а), подсказка 4
OO₁ ⊥ (BB₁C), ON ⊥ AA₁, а еще по условию AA₁ ⊥ (ABC), тогда ON будет параллельна плоскости (ABC)! Остается понять, что точка O₁ совпадает с точкой O. Для этого рассмотрите плоскость α, которая будет проходить через точку N параллельно плоскости (ABC), а также рассмотрите прямую l, которая перпендикулярна (BB₁C) и проходит через точку O₁. Что будет, если прямая l будет лежать в плоскости α?
Пункт а), подсказка 5
Действительно, такой ситуации быть не может, ведь тогда FB₁ ⊥ l, FB₁ ⊥ BC, а это две разные прямые, которые параллельны (ABC), тогда получается, что (BB₁C) ⊥ (ABC), а такого не может быть в нашей пирамиде! Тогда делаем вывод, что l пересекает α в одной точке, поэтому O₁ = O, что и хотелось показать. Теперь вовсе не составит труда найти сторону равностороннего треугольника BB₁C, если известно, что радиус его описанной окружности совпадает с радиусом сферы.
Пункт б), подсказка 1
Пусть O' – проекция O на (ABC), а B₁' – проекция B₁ на (ABC). Какой прямой в плоскости (ABC) будет принадлежать точка B₁'?
Пункт б), подсказка 2
Конечно, B₁' ∈ AB, можем даже узнать, в каком отношении точка O' будет делить отрезок FB₁' (покажите, что оно будет равно FO : OB₁). Тогда теперь можно будет найти длину отрезка B₁'F, нужно всего лишь показать, что треугольник BB₁'C равнобедренный, доказав равенство треугольников B₁B₁'B и B₁B₁'C. И нужный угол легко найдется, если рассмотреть угол между B₁B₁' || A₁A и нужной плоскостью.
Пункт б), подсказка 3
Пусть T – проекция O' на AB. Легко понять, что A₁B₁ = AB₁', тогда задача поиска A₁B₁ сведется к тому, что нужно будет найти AB₁' = AT + TB₁'. Найдите длину O’T, поработав с треугольником BB₁'C, а зная O’T, можно будет легко найти AT и TB₁', используя теорему Пифагора, а также факт, что AO' = ON.
![]()
Отметим точку в качестве вершины пирамиды, точку
в качестве центра
, точку
в качестве центра описанной окружности
треугольника
и
в качестве середины
. Так как
равносторонний, то
это еще и центр пересечения медиан, а
значит,
проходит через
и
и
. Так как
проходит через вершины треугольника
и
касается отрезка
в точке
, то
и
. Мы знаем, что
и поэтому
. Получается, что мы
знаем, что точка
лежит на плоскости
, проходящей через
и параллельной
, и лежит на прямой
, перпендикулярной
и проходящей через
. Значит, либо
принадлежит
, но тогда
перпендикулярна двум разным прямым
параллельным
(
и
) и тогда все три стороны перпендикулярны основанию, а такого не бывает, либо
и
пересекаются в одной точке и
. Тогда
и
(по формуле для равностороннего
треугольника).
![]()
Спроецируем точки и
на плоскость
. Тогда так как проекция
на
это
, то
и поэтому
.
Также можно заметить
.
Прямоугольные треугольники и
равны по катету и гипотенузе, поэтому
. Значит, высота в
равнобедренном треугольнике
равна
, так как
середина
и равна
.
Тогда
Значит, . Тогда
Пусть — проекция
на
. Тогда
и
. С другой стороны, поскольку
, то
. Отсюда
.
Ошибка.
Попробуйте повторить позже
Тетраэдр с остроугольными гранями вписан в сферу с центром
Прямая, проходящая через точку
перпендикулярно
плоскости
, пересекает сферу в точке
такой, что
и
лежат по разные стороны относительно плоскости
Прямая
пересекает плоскость
в точке
, лежащей внутри треугольника
Оказалось, что
и
.
Найдите величину
Первое решение.
Заметим, что точка равноудалена от точек
, так ее проекция на плоскость
совпадает с проекций точки
на эту
плоскость и является центром описанной окружности треугольника
.
Рассмотрим треугольники и
Они имеют пару равных сторон
и
, общую сторону
и равные углы
и
Из теоремы синусов следует, что эти треугольники либо равны, либо углы
и
дополняют друг друга до
Первая
ситуация невозможна, так как в случае равенства треугольников
и
точки
и
равноудалены относительно любой точки
на стороне
, но по условию
Значит,
Рассмотрим точку пересечения луча
со сферой
, описанной около тетраэдра
Заметим, что луч
лежит в
плоскостях
и
, а значит точка
лежит на описанных окружностях треугольников
и
Точка
равноудалена
относительно всех точек описанной окружности треугольника
в частности,
Из вписанности четырехугольника
следует, что
Раз
, то
- середина дуги
описанной окружности треугольника
, и значит
.
Используя выведенные ранее равенства углов, заключаем, что треугольники и
равны по второму признаку:
сторона – общая. Раз треугольники
и
равны, то вершины
и
равноудалены относительно любой точки на
стороне
в частности,
.
Осталось посчитать углы в плоскости Последовательно используя вписанность четырехугольника
, равнобедренность
треугольника
и теорему о внешнем угле для треугольника
, пишем
________________________________________________________________________________________
Второе решение.
Пусть луч пересекает сферу
, описанную около тетраэдра
, в точке
. По построению точки
верно соотношение
, которое влечет за собой равенство
. Аналогичными рассуждениями получаем, что
, и,
следовательно,
.
Обозначим точку пересечения прямой с плоскостью
, являющуюся центром описанной окружности треугольника
,
через
. Тогда
.
Рассмотрим трехгранные углы и
. В них совпадают плоские углы
и
, плоские углы
и
и двугранные углы при ребрах
и
прямые. Следовательно, соответствующие трехгранные углы
равны. А значит равны и плоские углы
. Отметим, что это равенство можно вывести и из теоремы
косинусов для трехгранных углов. Указанное равенство возможно в двух случаях: либо точка
лежит на серединном
перпендикуляре к
(точки
и
симметричны относительно
), либо точка
лежит на описанной окружности
треугольника
. Первый случай запрещен условием
, значит, имеет место второй. Тогда
и является центральным для угла
в описанной окружности треугольника
. В результате заключаем, что
.
Ошибка.
Попробуйте повторить позже
В основании треугольной пирамиды лежит прямоугольный треугольник
с гипотенузой
. Сфера
касается
плоскости основания пирамиды и касается всех трёх её боковых рёбер в их серединах. Пусть
— сфера, описанная около пирамиды
(a) Найдите расстояние между центрами сфер и
.
(b) Найдите отношение радиусов сфер и
.
(c) Пусть дополнительно известно, что Найдите объём пирамиды
.
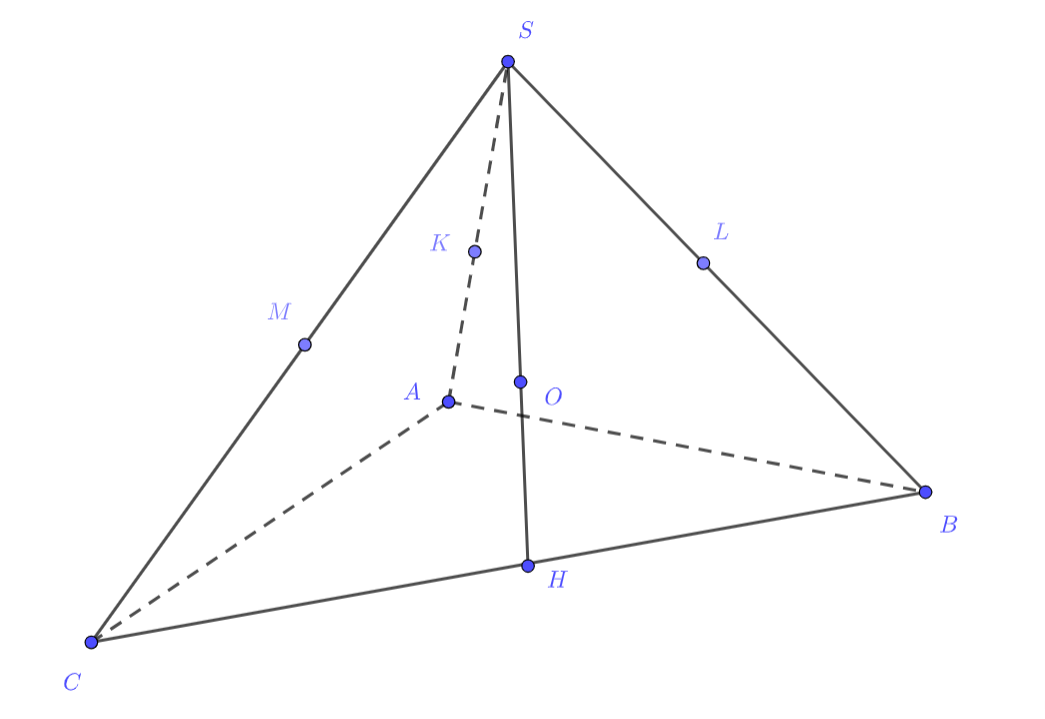
Пусть — центр сферы
— основания перпендикуляров, опущенных из точки
на ребра
соответственно;
—
высота пирамиды
и
— радиусы сфер
и
соответственно.
a) Поскольку точка лежит на серединном перпендикуляре к отрезку
она равноудалена от концов этого отрезка, т.е.
Аналогично
и
Значит,
поэтому точка
является центром сферы
. Следовательно,
расстояние между центрами сфер равно нулю.
b) Из равенства прямоугольных треугольников ,
и
— общая сторона) следует, что
Поскольку точки
— это середины боковых рёбер пирамиды, отсюда получаем, что боковые рёбра
равны между собой. Тогда высота пирамиды проходит через центр окружности, описанной около основания (действительно,
по катету и гипотенузе, откуда
). Но в пирамиде
боковые рёбра
также равны между собой как радиусы сферы
; значит, и её высота, проведённая из вершины
проходит через центр
окружности, описанной около основания. Таким образом, высота пирамиды
проходит через точку
Кроме того, точка
является центром окружности, описанной около основания. Поскольку треугольник
прямоугольный,
—
это середина гипотенузы
Так как отрезок
перпендикулярен плоскости основания, он равен радиусу
сферы
Для нахождения соотношения между радиусами рассмотрим прямоугольный треугольник Точка
— середина гипотенузы
на катете
находится точка
причём
,
Треугольники
,
и
равны по катету
и гипотенузе, следовательно,
Значит,
Тогда из треугольника
находим, что
c) поэтому треугольник
— равносторонний,
B равнобедренном треугольнике
известны боковые стороны
и угол при основании
Отсюда находим, что
.
По теореме Пифагора для треугольника
находим, что
поэтому
объём пирамиды
равен
Ошибка.
Попробуйте повторить позже
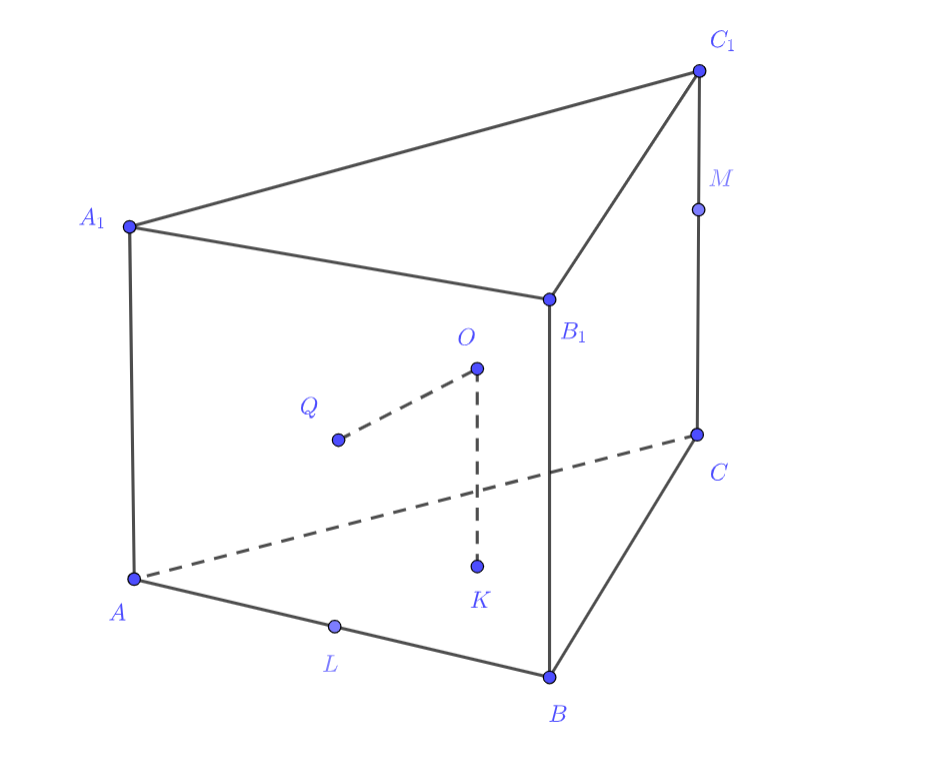
Введём обозначения: — центр грани
середина ребра
— центр сферы, описанной около пирамиды
(т.е.
— центр грани
);
— центр сферы, описанной около пирамиды
.
(a) 3начит, объём пирамиды
составляет две трети объёма призмы.
(b) Сторона равностороннего треугольника равна
, следовательно,
, как радиус описанной
окружности.
Рассмотрим прямоугольную трапецию . В ней известны стороны
и диагональ
По теореме
Пифагора из треугольника
находим, что
Опустим из точки
перпендикуляр
на отрезок
. Тогда
Отрезки и
равны как радиусы сферы. Решая получающееся уравнение, находим, что
Тогда площадь поверхности
призмы
Ошибка.
Попробуйте повторить позже
В сферу радиуса вписан параллелепипед, объём которого равен
Найдите площадь полной поверхности параллелепипеда.
Подсказка 1
У нас в сферу вписан параллелепипед. Тогда, на самом деле, он является прямоугольным. А где лежит центр нашей сферы?
Подсказка 2
Конечно, на главной диагонали d параллелепипеда! Давайте обозначим его ребра за a, b и c. Тогда с одной стороны, d²=a²+b²+c², с другой стороны, d²=12. Т.к. по условию объем равен 8, то abc=8. Хотелось бы найти a,b,c, но мы имеем всего 2 уравнения. Может, можно как-то схитрить?
Подсказка 3
Мы видим, что выражения a²+b²+c²=12 и abc=8 можно связать через неравенства о средних: 12=a²+b²+c²≥3(abc)^(2/3)=12. Подумайте, когда такое может получится, и завершите решение!
![]()
Поскольку около параллелепипеда описана сфера, этот параллелепипед — прямоугольный. Обозначим его рёбра, исходящие из одной
вершины, через ,
и
. Диагонали параллелепипеда равны диаметру описанной сферы, а объём равен
. Из условия задачи следует,
что
.
По неравенству Коши:
Так как равенство достигается только в случае , то
и площадь поверхности:
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде ребро
перпендикулярно плоскости
. Последовательность точек
строится следующим образом: точка
— центр сферы, описанной около пирамиды
, и для каждого натурального
точка
есть центр сферы, описанной около пирамиды
. Какую длину должно иметь ребро
, чтобы множество
состояло ровно из двух различных точек?
Подсказка 1
Т.к. SA ⊥ (ABC), то угол ∠SAB=90⁰. По условию ∠SCB=90⁰. Это означает, что наши точки лежат на сфере, с диаметром SB. А на какой прямой лежат центры O₁, O₂, ...?
Подсказка 2
Правильно, на перпендикуляре к плоскости (ABC), проведенной в точке X- середине AB. Мы хотим, чтобы множество наших центров состояло всего из двух точек. Давайте тогда поймем, когда O₃ совпадает с кем-то из O₁, O₂.
Подсказка 3
Ясно, что с O₂ она совпадать не может. Т.к. O₁- середина SB, то и O₃- середина SB. Т.к. O₃ равноудалена от A, B, C и O₂, а O₂ равноудалена от A, B, C и O₁=O₃, то AO₃BO₂- ромб с углом 60°. Я думаю, что вы сможете закончить решение!
![]()
Применим теорему о трех перпендикулярах. В силу того, что и
, получим, что проекция
на плоскость
перпендикулярна
, то есть
Заметим, что середина гипотенузы - точка
это центр описанной окружности прямоугольного треугольника
.
Аналогично середина гипотенузы
- точка
- центр описанной окружности прямоугольного треугольника
. Тогда если
провести перпендикуляр к плоскости
в точке
и перпендикуляр к плоскости
в точке
, то центр описанной
окружности
пирамиды
- точка пересечения этих перпендикуляров. Но перпендикуляр к плоскости
в точке
совпадает с прямой
. То есть точка
и есть точка
.
При этом на прямой (перпендикуляр к плоскости
в точке
) будут лежать все
в силу того, что
- ГМТ точек
равноудаленных от
То есть точка - центр треугольной пирамиды
- опять-таки должна лежать на прямой
![]()
Хотелось бы добиться того, чтобы (
по очевидным причинам). Но тогда
. То есть середина гипотенузы
равноудалена от точек
. Так же точка
равноудалена от точек
. Но тогда
должен быть ромбом, при
этом его диагональ
должна быть равна стороне. Понятно, что тогда
. Значит, что
, то есть



