Отношение отрезков в стерео: подобие, Фалес, Менелай
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде на ребре
взята точка
так, что
на ребре
взята точка
так, что
и на ребре
точка
такая, что
В каком отношении отрезок
делится плоскостью
Источники:
Подсказка 1
У нас в задачке даны отношения отрезков. В лоб как-то считать не очень хочется... Может, применить метод масс?
Подсказка 2
Мы хотим понять, в каком отношении плоскость CDP делит QR. Если мы добьемся того, чтобы центр масс G тетраэдра лежал одновременно в плоскости CDP и на отрезке QR, то QG/GR- и будет искомым отношением. Теперь надо расставить массы, чтобы эти условия выполнялись...
Подсказка 3
Чтобы G лежал в плоскости CDP достаточно, чтобы центр масс концов отрезка AB совпадал с P. Тогда: m(A)/m(B)=PB/PA=2. А как сделать так, чтобы G лежал на отрезке QR?
Подсказка 4
Достаточно, чтобы центр масс концов отрезка CB попадал в R, а отрезка AD- в Q. Тогда: m(C)/m(B)=BR/CR=3 и m(A)/m(D)=DQ/AQ=3/2. Какие массы надо взять, чтобы выполнялись все отношения?
Подсказка 5
Можно, например, взять m(A)=6, m(B)=3, m(C)=9 и m(D)=4. Тогда после группировки в Q будет масса 10, а в R- 12. Посчитайте отношение QG/GR и радуйтесь!
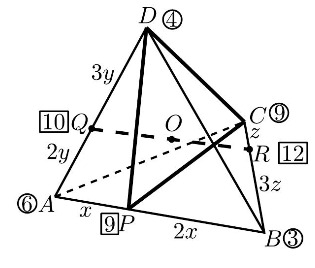
Применим метод масс. Поместим в вершины пирамиды такие массы:
Если из точек и
убрать обе массы и поставить их сумму в точку
то центр тяжести всей системы не изменится, поэтому он
будет лежать в плоскости
С другой стороны, если убрать две массы из точек и
и вместо них поставить суммарную массу
в точку
а вместо
точек
и
поставить суммарную массу
в точку
то центр тяжести также не изменится и значит он будет находиться на
отрезке
Таким образом, центр тяжести данной системы будет расположен в точке пересечения прямой и плоскости
то есть в точке
Значит,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




