Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Отношение отрезков в стерео: подобие, Фалес, Менелай

Тема Счёт отрезков в стерео

Отношение отрезков в стерео: подобие, Фалес, Менелай

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела счёт отрезков в стерео

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83311

Медианы оснований треугольной призмы $ABCA B C 1 1 1$ пересекаются в точках $O$ и $O 1$ соответственно. На отрезке $OO 1$ взята точка $P$ так, что $O1P :PO = 3:5$ . Через точку $P$ проведена прямая параллельная диагонали $A1C$ боковой грани призмы. Найти длину отрезка этой прямой, расположенного внутри призмы, если длина диагонали $A1C$ равна 2.

Источники: Росатом - 2024, региональный вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Рассмотрим сечение призмы XYZT, проходящее через OO₁ и параллельное грани ACC₁A₁. Прямая, проходящая через точку Р и параллельная А₁С, будет лежать как раз в этом сечении. А искомый отрезок - это часть этой прямой, ограниченная четырехугольником XYZT. А какой фигурой является XYZT? Как относятся ее стороны к сторонам призмы?

Подсказка 2

Верно, XYZT - параллелограмм. ZT = XY = A₁A, XT = YZ = 2/3 * AC, так как точка пересечения медиан делит медианы в отношении 2 к 1. Теперь нужно подумать, с помощью чего мы можем "перенести" плоскость ACC₁A₁ на плоскость XYZT?

Подсказка 3

С помощью гомотетии! Сделаем гомотетию в точке В₁ с коэффициентом 2/3. Подумайте, куда перейдут точки, лежащие в плоскости ACC₁A₁.

Подсказка 4

Например, точка А₁ перейдет в точку Х. Постройте прямые, параллельные А1С, через точки Х и Z. Чему будут равны отрезки этих прямых, отграниченные параллелограммом XYZT? Равна ли искомая прямая этим отрезкам?

Показать ответ и решение

Рассмотрим сечение призмы $XY ZT$ , проходящее через $OO 1$ и параллельное грани $ACC A 1 1$ . Это параллелограмм, а $OO 1$ — его средняя линия.

Сделаем гомотетию в точке $B1$ с коэффициентом $2 3$ . Тогда точки $A1$ и $C1$ перейдут в $X$ и $T$ , потому что точка пересечения медиан делит медиану в отношении $2$ к $1$ . Точка $Q$ перейдёт в точку $Q1$ , делящую отрезок $OO1$ в отношении $2$ к $1$ (до гомотетии отрезок $P Q$ был половиной $PR$ , а после он перешёл в $XQ1$ , который равен $1 3PR$ ). При этом прямая $XQ1$ будет пересекать отрезок $TZ$ в точке $W$ , поскольку в параллелограмме $ACC1A1$ прямая $A1C$ пересекает вершину $C$ , а в параллелограмм $XYZT$ отличается от $ACC1A1$ лишь тем, что длины сторон $YZ$ и $XT$ короче, а значит, точка пересечения прямой $XQ1$ с прямой $TZ$ будет лежать ниже точки $Z$ .

$PIC$

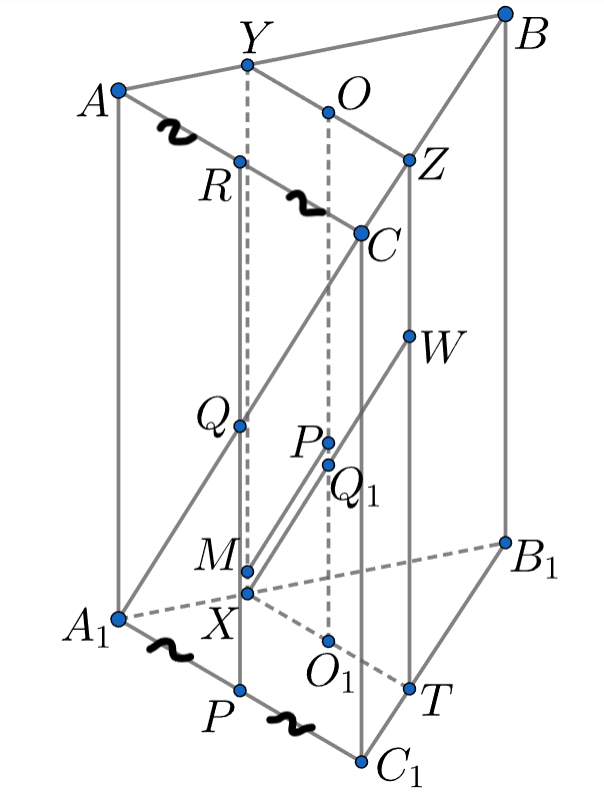
Аналогично, прямая, проходящая через $Z$ параллельно прямой $A1C$ будет делить $OO1$ в отношении $2$ к $1$ , но уже считая от точки $O$ , и она будет проходить через отрезок $XY$ . Значит, прямая $MP$ будет лежать между этими двумя прямыми и также проходить через отрезок $TZ$ . Значит, отрезок нужной прямой — это отрезок прямой $MP$ , содержащийся в параллелограмме $XY ZT$ .

Поскольку $MP ∥ XW$ , длина этого отрезка будет равна $XW$ . Отрезок $XQ1$ — образ $AQ$ при гомотетии, значит, он равен $23AQ = 23$ .

Также $XQ1 = Q1W$ , то есть искомая длина — $43$ .

Ответ:

$4 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#83740

Параллелограмм $ABCD$ является основанием пирамиды $SABCD.$ Точки $M,N$ и $P$ лежат на рёбрах $SA,SD$ и $SC$ соответственно, причём

SM :MA = 1:2, SN :ND = 1:3, SP :PC =1 :4

В каком отношении плоскость $MNP$ делит ребро $SB?$

Источники: Звезда - 2024, 11.1 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Построить точку пересечения плоскости MNP и ребра SB сразу так сложно. Кажется, не хватает какой-нибудь точки на MP, чтобы провести через неё и N прямую, пересекающую ребро SB в искомой точке (пусть K).

Подсказка 2

Да это же точка, получаемая пересечение MP и SO, где SO — пересечение плоскостей BSD и ASC, назовём её Т. Точку ввели, а как она делит SO — не узнали. А хотелось бы, потому что её можно рассмотреть и для △ASC (а мы знаем про то как делят его стороны M и P), и для △BSD (содержащий интересующую нас точку K).

Подсказка 3

Отношение ST : NO можно найти, рассмотрев △ASC. А ещё же у нас есть отношение AO : OC (подумайте, чем является точка O для основания). Часто, когда мы видим отношения отрезков, хочется применить теорему Фалеса, только вот нам не хватает несколько параллельных прямых... Какие можно провести, чтобы использовать оба упомянутых отношения на сторонах SA и AC?

Подсказка 4

В предыдущей подсказке попробуйте провести прямые из A и O параллельно MP. С помощью теоремы Фалеса можно найти отношение ST : NO. Если Вы всё правильно посчитали, то не составит труда, используя уже упомянутую теорему, найти отношение SK : KB.

Показать ответ и решение

Пусть плоскости $BSD$ и $ASC$ пересекаются по прямой $SO.$ Рассмотрим треугольник $ASC.$ Пусть $T = MP ∩ SO.$

$PIC$

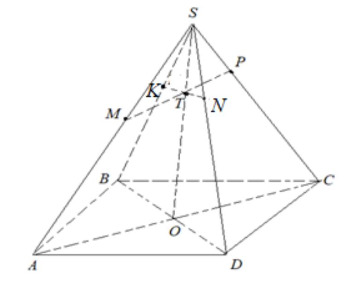
В треугольнике $ASC$ проведём прямые $AL$ и $OQ$ параллельные $MP.$

$PIC$

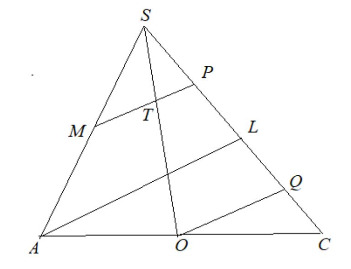
По теореме Фалеса имеем

SPPL-= SMMA- = 12, LQQC-= AOOC- =1

Учитывая, что $SP :PC =1 :4,$ получаем, что

ST-= 1 TO 3

Пусть $K = NT ∩ SB.$ Так как

SN :ND = ST :TO =1 :3,

то в силу теоремы Фалеса прямые $BD$ и $NK$ параллельны, и, следовательно,

SK :KB =1 :3

Ответ: 1:3

Ошибка.
Попробуйте повторить позже

Задача 3#86474

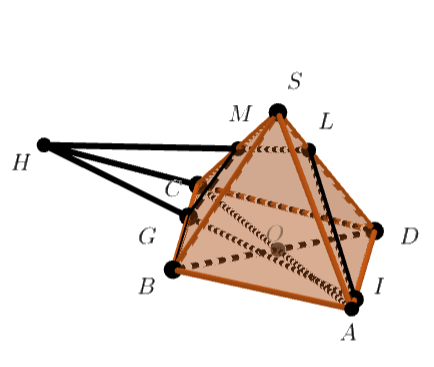
Основанием четырехугольной пирамиды $SABCD$ является параллелограмм $ABCD$ со сторонами $AB =2√3,AD = 4√3$ и углом $A$ , равным $∘ 60$ . Высотой пирамиды $SABCD$ является отрезок $SO$ , где $O$ - точка пересечения диагоналей параллелограмма $ABCD, SO = 1$ . Найдите площадь сечения пирамиды $SABCD$ плоскостью, параллельной медиане $SE$ боковой грани $SAB$ и проходящей через середину ребра $SC$ и середину отрезка $AO$ .

Источники: ШВБ - 2024, 11.5 (см. olymp.bmstu.ru)

Подсказки к задаче

Подсказка 1

То, что в условии нам даны все длины, может подтолкнуть к тому, что это очень техническая задача. Здесь придется много считать и не бояться больших и страшных дробей. Первым делом нужно построить сечение. Поищите точку, принадлежащую сечению, на плоскости ABCD.

Подсказка 2

Теперь рассмотрим саму плоскость ABCD. У нас есть прямая, лежащая в этой плоскости и принадлежащая сечению. Где эта прямая пересекает прямые, содержащие стороны параллелограмма ABCD? Найдите отношения с помощью теоремы Менелая и подобия.

Подсказка 3

Пусть эта прямая пересекает прямые AB,BC,CD, AD в точках F,G,H,I соответственно. Пусть L - точка, в которой прямая HM пересекает ребро SD. Тогда искомое сечение это LMGI. Найдем его площадь как разность площадей треугольников LHI и MGH. А как найти их площади? Много считать длины сторон и отношения, используя теоремы Менелая, Герона, Пифагора, косинусов.

Показать ответ и решение

Пусть $M$ — середина ребра $SC,$ а точка $K$ - середина отрезка $AO$ . Рассмотрим плоскость $(CSE)$ . Так как плоскость сечения параллельна медиане $SE$ и проходит через точку $M$ , построим прямую $MT ||SE$ в плоскости $(CSE )$ . Тогда $MT$ - средняя линия в $CSE$ , а $T$ середина $CE$ .

Теперь нам известны три точки сечения: $T,M, K$ . Рассмотрим основание пирамиды $ABCD$ и посмотрим, как прямая $TK$ пересекает стороны основания. Пусть эта прямая пересекает прямые $AB,BC,CD, AD$ в точках $F,G,H,I$ .

$PIC$

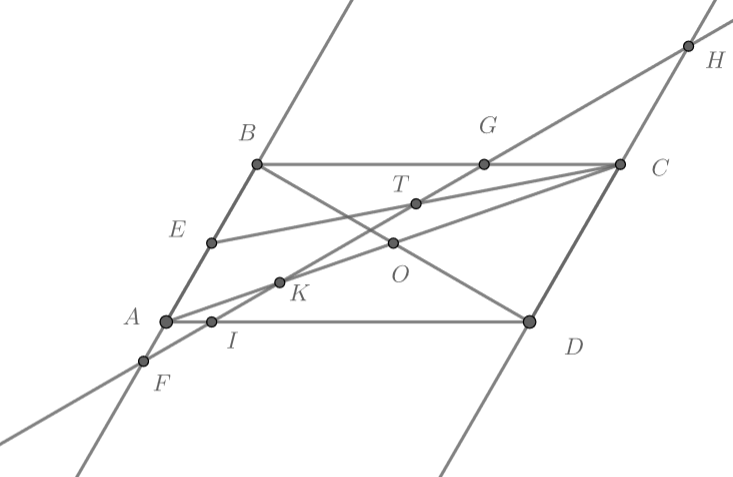
Из теоремы Менелая для треугольника $ACE$ получаем, что

EF-= CK-⋅ TE-= 3 FA AK CT 1

Так как $EA = 1AB 2$ , то $FA = 1AB 4$ .

Далее замечаем, что $△F AK ∼ △HCK$ . Тогда

AF- AK- 1 HC = CK = 3

Откуда $3 HC =3AF = 4AB$ .

Из подобия $△FAI ∼△HDI$ получаем

AI AF 1 ID-= DH-= 7

То есть $AI = 18AD$ .

Аналогично из подобия $△FBG ∼ △HCG$ получаем

BG-= FB-= 5 GC CH 3

То есть $BG = 58BC$ .

Проведем $GG ′||CD$ , где $G′$ - точка на $AD$ . Тогда

GG ′ =AD = 2√3;G′I =AD − 3BC − 1BC = BC-= 2√3 8 8 2

И $∠GG ′I =180∘− ∠A= 120∘$ . Тогда из теоремы косинусов для треугольника $GG ′I$ получим $IG = 6$ .

$PIC$

Пусть $L$ - точка, в которой прямая $HM$ пересекает ребро $SD$ . Тогда из теоремы Менелая для $△CSD$ и прямой $HM$ получим:

7 DL-= CM- ⋅ DH =1⋅-4CD = 7 SL SM CH 34CD 3

Далее из теоремы Менелая для $△DHL$ имеем:

HM CH SD 5 ML--= DC-⋅-SL = 2.

В силу параллельности прямых $BC$ и $AD$ имеем $HHGI-= 37$ , откуда $HG = 92,HI = 212$ . По теореме косинусов для $△ABD$ имеем $BD = 6$ , то есть $OD = 3$ . Из теоремы Пифагора для треугольника $SOD$ получаем $SD =√10-$ , откуда $7√10 DL = 10$ . По теореме косинусов для $△ADC$ имеем $√-- 2 21$ , а значит $√ -- TC = 21$ . По теореме Пифагора для $△SOC$ вычислим $√-- SC = 22$ . Заметим, что для треугольника $SDC$ выполняется теорема Пифагора, то есть угол $SDC$ прямой. С помощью теоремы косинусов для треугольника $SAD$ вычислим $3√30 cosSDA = 20$ . Теперь через теоремы косинусов для треугольников $LDI$ и $LDH$ вычислим длины отрезков $7√10- 7√85- IL = 5 ,LH = 10$ . Далее по теореме Герона получаем $147- S△ILH = 20$ .

Заметим, что $1 1 5 3 15 S△MHG = 2sin∠MHG ⋅MH ⋅GH = 2sin∠MHG ⋅7HL⋅ 7HI = 49S△HLI$ . Значит, $34 34 147 51 SLMGI = S△LHI − S△MHG = 49S△LHI = 49-⋅20 = 10$ .

Ответ: 5.1

Ошибка.
Попробуйте повторить позже

Задача 4#91958

Плоскость $π$ перпендикулярна ребру $SA$ правильной треугольной пирамиды $ABCS$ с вершиной $S$ и основанием $ABC$ , делит это ребро в отношении $1:2$ (считая от вершины $S$ ) и проходит через середину ребра $SB$ . Найдите угол между плоскостью $π$ и плоскостью основания пирамиды.

Источники: ДВИ - 2024, вариант 241, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте построим сечение MNK (M∈AS, N∈SB, K∈SC) пирамиды SABC плоскостью π. Обозначим AS = 6х и попробуем выразить все отрезки на рисунке через х (для этого можно воспользоваться теоремой косинусов для треугольника △ASB, ведь cos∠ASB мы можем без проблем найти, так как на рисунке есть очень много прямоугольных треугольников)

Подсказка 2

Проведём LN — среднюю линию треугольника △ASB, обозначим за Р середину NK. Какой угол требуется найти в задаче?

Подсказка 3

Конечно, угол ∠MPL! Так как мы уже знаем соотношение практически всех отрезков, мы можем без труда найти значение синуса этого угла)

Показать ответ и решение

Первое решение.

Пусть $π$ пересекает $AS,$ $BS$ и $CS$ в точках $P,$ $R$ и $Q$ соответственно (то есть $π = (PQR )).$ Тогда по условию $SR = RB$ и $AP = 2PS.$ Пусть $M$ — середина $BC.$ Тогда пирамида $SABC$ симметрична относительно плоскости $(SAM ).$ Поскольку $π$ пересекает ребро $SB$ в середине, то в силу симметрии эта плоскость пересекает $CS$ тоже в середине, поэтому $QC = QS.$

$PIC$

Пусть $K$ — середина $AP.$ Тогда $PS =P K = AK,$ так как $AP = 2P S.$ Тогда, поскольку $SP :PK = SR :RB,$ то $PR$ и $KB$ параллельны. Аналогично можно доказать, что $RQ$ и $BC$ параллельны. Таким образом, $π$ и $(KBC )$ — параллельные плоскости, поэтому требуемый в задаче угол равен углу между $(KBC )$ и $(ABC ).$

Так как по условию $π$ и $AS$ перпендикулярны, то $(KBC )$ и $AS$ перпендикулярны, то есть $BK$ и $CK$ перпендикулярны $AS.$ Снова применив соображение симметрии, получаем, что $KB = KC,$ то есть $△KBC$ — равнобедренный, и $KM$ — его высота, поскольку $M$ является серединой $BC.$ Так как $ABC$ — правильный треугольник (по условию $SABC$ — правильная пирамида), то $AM$ — тоже высота в треугольнике $ABC.$ Таким образом, $KM$ лежит в плоскости $(KBC )$ и перпендикулярно $BC,$ а $AM$ лежит в плоскости $ABC$ и перпендикулярно $BC.$ Эти плоскости пересекаются по прямой $BC.$ Таким образом, нужный угол по определению равен $∠KMA.$

Пусть $AB = BC = AC = 2a.$ Тогда $BM =MC =a,$ так как $M$ — середина $BC.$ По теореме Пифагора из треугольника $ABM$ получаем $AM = √3a.$ По теореме Пифагора из треугольника $KSB$ получаем $KB2 = 5x2.$ С другой стороны, по теореме Пифагора из треугольника $AKB$ имеем $KB2 = 4a2− x2.$ Таким образом, $4a2 − x2 = 5x2,$ то есть $∘ -- x = 23a.$

Так как $KBC$ и $AS$ перпендикулярны, то $KM$ и $AS$ перпендикулярны. Из прямоугольного треугольника $AKM :$

∘ -- x 2a √2- sin ∠AMK = √3a-= √33a-= -3-

Таким образом, $√- ∠AMK = arcsin-23 .$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Пусть $π$ пересекает $AS$ в точке $H,$ $BS$ — в точке $M.$ Пусть $AS = CS =BS = 6x.$ Тогда из условия следует, что $SH =2x,$ $AH = 4x,$ так как $SH :AH = 1:2.$ $M$ — середина $SB,$ поэтому $SM = SB =3x.$

$PIC$

По теореме Менелая для треугольника $ASC$ и прямой $HT :$

4x 3x CT- 2x ⋅3x ⋅TA = 1

Таким образом, $TA =2CT,$ поэтому $AC = CT.$ Пусть $AC = y.$ По теореме Менелая для треугольника $AHT$ и прямой $SC :$

y TM 2x y ⋅MH--⋅6x = 1

Таким образом, $TM = 3MH.$ Так как $AS$ по условию является перпендикуляром к плоскости $π,$ то $T H$ и $AS$ перпендикулярны. Тогда по теореме Пифагора из треугольника $SMH$ получаем $√- HM = 5x.$ То есть $√- TM = 3 5x.$ По теореме Пифагора для треугольника $AHT :$

16x2 +80x2 = 4y2

Таким образом, $√- y = 2 6x.$ Пусть $O$ — основание высоты пирамиды $SABC.$ Углы между плоскостями равны углам между перпендикулярами к ним, поэтому

∠(π,(ABC )) =∠(SA,OS)

Из прямоугольного треугольника $ASO$ получаем $sin∠ASO = AAOS-.$ Так как $O$ — точка пересечения медиан правильного треугольника $ABC,$ то $√- √- AO = -33 y = 2 2x.$ Тогда

√- √- sin∠ASO = AO-= 2-2x = -2- AS 6x 3

Таким образом, $∠ASO = arcsin√2. 3$

______________________________________________________________________________________________________________________________________________________

Третье решение.

Пусть искомый угол это $φ.$ Обозначим пересечение плоскости $π$ с ребрами $SA, SB, SC$ точками $M, N, K$ соответственно. $N$ — середина ребра $SB,$ следовательно, $K$ тоже середина ребра, так как пирамида правильная. По условию $NM ⊥ SA, KM ⊥ SA.$ Обозначим длину $SA$ как $6x,$ тогда получаем, что

SM = 2x, AM = 4x, SN = NB = SK =KC =3x

$PIC$

В треугольнике $MSN :$

2x 2 cos∠MSN = 3x = 3

Тогда по теореме косинусов для треугольника $ASB$ получаем

2 2 2 2 2 2 2 AB = AS + SB − 2⋅AS⋅SB ⋅cos∠MSN = (6x) +(6x) − 2⋅6x⋅6x⋅3 =24x

√- AB = 2x 6

Обозначим середину ребра $SA$ точкой $L.$ Тогда треугольник $LNK$ правильный, так как треугольник $ABC$ правильный, а также плоскость $(LNK )$ параллельна плоскости основания. $LN$ — средняя линия в треугольнике $ASB,$ следовательно, $LN =x√6.$ Обозначим точкой $P$ середину $NK.$ В треугольнике $LNK :$

LN √3 3x√2- LP = --2-- =--2-

так как треугольник $LNK$ правильный.

Так как плоскость $(LNK )$ параллельна плоскости основания, то найдем угол между этой плоскости и плоскости $π.$

MP ⊥ NK, LP ⊥ NK =⇒ ∠LPM = φ

Так как $L$ — середина, то $LM =x.$ В прямоугольном треугольнике $LP M (MP ⊥SA )$ находим, что

LM x √2 sin∠LPM = -LP = 3x√2-= -3- 2

Тогда

√- ∠LMP = φ =arcsin -2- 3

Ответ:

$arcsin√2 3$

Ошибка.
Попробуйте повторить позже

Задача 5#69437

В параллелепипеде $ABCDA B C D 1 1 1 1$ точка $T−$ середина ребра $BB ,P 1$ лежит на ребре $AD$ так, что $AP :PD = 1:4.$

(a) Постройте сечение параллелепипеда плоскостью $C1TP.$

(b) Найдите отношение, в котором секущая плоскость делит ребро $DD1.$

Подсказки к задаче

Подсказка 1

Для того, чтобы построить сечение, нужно пересечь наш параллелепипед плоскостью. Давайте вспомним, что плоскость пересекает другую плоскость по прямой. А прямая строится по двум точкам. Как мы это можем использовать?

Подсказка 2

Давайте попробуем пересечь нашей плоскостью грань C₁B₁BC. Наша плоскость и данная грань пересекаются по прямой, а еще мы уже знаем две точки - C₁ и T, лежащие в пересечении. Значит, наша плоскость пересекает эту грань по какой прямой?

Подсказка 3

Верно, по прямой через точки C₁ и T! Проведем ее до пересечения с ребром CB (точка L) и попробуем найти пересечение нашей плоскости со следующей гранью - ABCD. Мы снова уже знаем две точки, которые точно лежат в пересечении - L и P! Значит, можно проделать тот же самый трюк. Осталось доделать сечение теми же методами!

Подсказка 4

Для того, чтобы найти отношение, было бы здорово использовать утверждения о том, как точки T и P делят стороны, а еще - найти подобных треугольников, чтобы эти знания использовать.

Подсказка 5

Например, треугольники LBT и LCC₁ - подобны, и мы даже знаем, с каким коэффициентом (вспомните, как точка T делит отрезок BB₁). Для удобства можно за х обозначить BB₁, и за y обозначить DA. После этого мы можем рассмотреть подобие треугольников MPA и MBL. И у нас еще есть подобие ODP, PAM. Пользуясь ими тремя и аккуратным счетом, можно достигнуть успеха!

Показать ответ и решение

(a) Проведем прямую $C T 1$ , пусть она пересечет $CB$ в точке $L$ . Далее проведем прямую $LP$ , пусть она пересечет $BA$ в точке $M$ и прямую $CD$ в точке $O$ . Затем проведем отрезок $OC1$ , пусть он пересечет $DD1$ в точке $N$ . Плоскость $C1TMP N$ и будет искомым сечением

$PIC$

(b) Пусть отрезки $B1T$ и $TB$ равны $y$ , а отрезок $CB =x$ . Тогда $CC1 = 2y$ . Заметим, что

△CC1L ∼ △BT L =⇒ C1C-= CL- =⇒ T B BL

=⇒ x-+BL-= 2 =⇒ BL= x BL

Так как $DP- 4x x P A =4 =⇒ DP = 5 , PA = 5.$

Пусть $AM = z$ . Заметим, что

BL MB △PAM ∼△MBL =⇒ PA-= AM--=5 =⇒

=⇒ MB = 5AM =5z =⇒ AB =DC =6z

Заметим, что $DP- OD- △ODP ∼△P AM =⇒ PA = AM = 4 =⇒ OD = 4AM = 4z$ .

Далее воспользуемся тем, что $△ODN ∼ △OCC1$

OD ND 4 ND 4y OC- =CC1- =⇒ 10 =-2y- =⇒ ND = -5

Тогда

D1N =2y− 4y= 6y =⇒ D1N-= 3 5 5 ND 2

Ответ: 3:2

Ошибка.
Попробуйте повторить позже

Задача 6#69820

В треугольной пирамиде $ABCD$ на ребре $AB$ взята точка $P$ так, что $AP :P B =$ $1 :2,$ на ребре $AD$ взята точка $Q$ так, что $AQ :QD = 2:3$ и на ребре $BC$ точка $R$ такая, что $BR :RC =3 :1.$ В каком отношении отрезок $QR$ делится плоскостью $CDP ?$

Источники: САММАТ-2023, 11.1 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

У нас в задачке даны отношения отрезков. В лоб как-то считать не очень хочется... Может, применить метод масс?

Подсказка 2

Мы хотим понять, в каком отношении плоскость CDP делит QR. Если мы добьемся того, чтобы центр масс G тетраэдра лежал одновременно в плоскости CDP и на отрезке QR, то QG/GR- и будет искомым отношением. Теперь надо расставить массы, чтобы эти условия выполнялись...

Подсказка 3

Чтобы G лежал в плоскости CDP достаточно, чтобы центр масс концов отрезка AB совпадал с P. Тогда: m(A)/m(B)=PB/PA=2. А как сделать так, чтобы G лежал на отрезке QR?

Подсказка 4

Достаточно, чтобы центр масс концов отрезка CB попадал в R, а отрезка AD- в Q. Тогда: m(C)/m(B)=BR/CR=3 и m(A)/m(D)=DQ/AQ=3/2. Какие массы надо взять, чтобы выполнялись все отношения?

Подсказка 5

Можно, например, взять m(A)=6, m(B)=3, m(C)=9 и m(D)=4. Тогда после группировки в Q будет масса 10, а в R- 12. Посчитайте отношение QG/GR и радуйтесь!

Показать ответ и решение

$PIC$

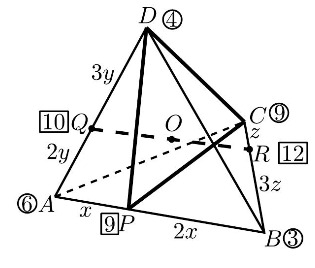
Применим метод масс. Поместим в вершины пирамиды такие массы: $A − 6,B − 3,C − 9,D− 4.$

Если из точек $A$ и $B$ убрать обе массы и поставить их сумму в точку $P,$ то центр тяжести всей системы не изменится, поэтому он будет лежать в плоскости $CDP.$

С другой стороны, если убрать две массы из точек $A$ и $D$ и вместо них поставить суммарную массу $6+4 =10$ в точку $Q,$ а вместо точек $B$ и $C$ поставить суммарную массу $3+9 =12$ в точку $R,$ то центр тяжести также не изменится и значит он будет находиться на отрезке $QR.$

Таким образом, центр тяжести данной системы будет расположен в точке пересечения прямой $QR$ и плоскости $CDP,$ то есть в точке $O.$

Значит, $QO :OR =12:10= 6:5.$

Ответ:

$6 :5$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#64686

Дан куб $ABCDA ′B′C′D ′.$ Через середины его ребер $AA′,C′D ′$ и через центр грани $BCC ′B′$ проведена плоскость, пересекающая диагональ $′ DB$ куба в точке $O$ . Найдите отношение $DO$ : $′ OB .$

Источники: Вместо ЕГЭ - 2022, вариант ЕМ222, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Построение этого сечения не выглядит тривиальной задачей. Разберёмся для начала, какие точки этой плоскости нам нужны, чтобы отыскать искомое соотношение. Удобно будет работать с пересечением этой плоскости (назовем ее π) и диагональной (BDD'). Значит нам точно понадобится пересечение π c рёбрами BB' и DD'.

Подсказка 2

Можно заметить, что середина ребра C'D' и центр грани BCC'B' лежат в плоскости диагонального сечения (ABC'). Рассмотрите эту плоскость и поработайте с подобными треугольниками, чтобы определить точку пересечения плоскости π с прямой АВ — зная её, мы сможем посчитать и положение точки пересечения π с ребром BB'.

Подсказка 3

Определить точку пересечения π и DD' тоже не получится в один шаг: удобно это сделать сначала рассматривая всё ту же плоскость (ABC') и прямую AD' в ней. А потом можно будет высчитать и положение точки на DD'.

Подсказка 4

Осталось рассмотреть плоскость (BDD') и имеющуюся у нас теперь прямую её пересечения с π. Поработайте с подобными треугольниками, чтобы отыскать то самое соотношение DO:OB'

Показать ответ и решение

$PIC$

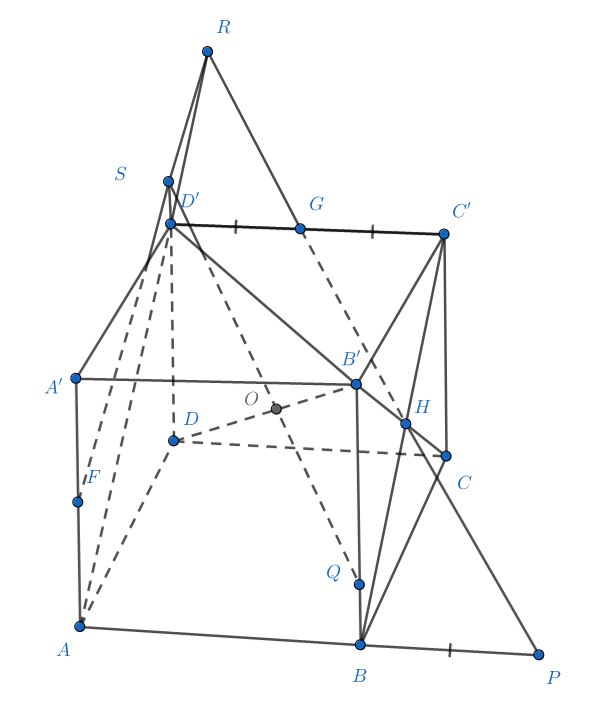
Обозначим середины ребер $AA′,C′D ′$ и центр грани $BCC ′B′$ через $F,G,H$ , соответственно. Обозначим также через $π$ плоскость $FGH$ .

Найдем точку $Q$ пересечения плоскости $π$ и прямой $BB′$ . Точки $G,H,A,B$ лежат в плоскости $ABC ′$ , следовательно прямые $GH$ и $AB$ пересекаются. Пусть $P$ - точка их пересечения. Тогда $BP = C′G= 12AB$ , поскольку треугольники $HC′G$ и $HBP$ равны. Точки $P$ и $F$ принадлежат $π$ , следовательно, прямая $FP$ есть прямая пересечения плоскости $ABB ′$ с $π$ . То есть $Q$ лежит на отрезке $BB ′$ . Из подобия треугольников $APF$ и $BPQ$ следует, что $BQ = 13AF = 16BB ′$ . Следовательно, $QB ′ = 56BB′$ .

Найдем теперь точку $S$ пересечения плоскости $π$ и прямой $DD ′$ . Прямая $GH$ лежит в плоскости $ABC ′$ , равно как и прямая $AD′$ . Обозначим через $R$ точку пересечения этих прямых. Из подобия треугольников $RAP$ и $RD ′G$ следует, что $RD ′ = 13RA$ . Точки $R$ и $F$ принадлежат $π$ , следовательно, прямая $F R$ есть прямая пересечения плоскости $ADD ′$ с $π$ . То есть $S$ лежит на продолжении отрезка $DD ′$ за точку $D ′$ . Из подобия треугольников $ARF$ и $D′RS$ следует, что $D′S = 1AF = 1DD ′ 3 6$ . Следовательно, $SD = 7DD ′ 6$ .

Прямая $SQ$ есть прямая пересечения плоскости $DBB ′$ с $π$ , то есть она проходит через $O$ . Треугольники $SDO$ и $QB′O$ подобны с коэффициентом подобия $7 5$ . Следовательно, $DO :OB′ =$ $7:5$ .

Ответ:

$7 5$

Ошибка.
Попробуйте повторить позже

Задача 8#63813

Дана треугольная призма $ABCA ′B ′C′$ с основанием $ABC$ и боковыми рёбрами $AA′,BB′,CC ′$ . На диагоналях $AB′,BC′,CA ′$ отмечены точки $D,E,F$ соответственно. Найдите отношение, в котором плоскость $DEF$ делит отрезок $′ AA$ , если $′ ′ AD :DB =1 :1,BE :EC = 1:2$ , $′ CF :FA =1 :3.$

Источники: ДВИ - 2020, вариант 201, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Надо как-то разобраться с плоскостью DEF и отрезком AA'. Для этого можно, например, отыскать какую-нибудь плоскость, в которой будут две точки нашей плоскости DEF и отрезок AA'. Потенциально это могут быть плоскости ABB'A' и ACC'A', в которых есть по одной точке из плоскости DEF. Как бы нам найти еще какую-нибудь точку?

Подсказка 2

Грани нашей призмы являются параллелограммами, поэтому D- не только середина AB', но и A'B. Стало быть точка D лежит еще и в плоскости BA'C', в которой лежит еще и точка E. Тогда если провести прямую ED, она пересечет луч C'A' в какой-то точке P. Ураааа! Вторая точка найдена. Осталось только понять в каком отношении FP делит A'A. Для начала поймите, как относятся PA' и A'C'...

Подсказка 3

С помощью теоремы Менелая вы легко убедились, что PA'=A'C'. У нас осталась совсем простая задачка: В параллелограмме ACA'P точка F делит A'C в отношении 3:1, а нужно найти как PF делит AA'.

Подсказка 4

Если вы еще не решили ее, то советую продлить отрезок PF до пересечения с AC в точке Q и посмотреть, как относятся PA' и AQ.

Показать ответ и решение

Точки $D$ и $F$ лежат в плоскости $BCA ′$ . Обозначим через $G$ точку пересечения прямой $DF$ с прямой $BC$ .

$PIC$

Из того, что $AD :DB ′ =1 :1,CF :FA ′= 1:3$ , следует, что $GC = 12BC$ . Обозначим через $H$ точку пересечения прямой $GE$ с прямой $CC ′$ . Из того, что $GC = 12BC$ и $BE :EC ′ = 1:2$ , следует, что $CH = 17CC ′$ . Обозначая через $K$ точку пересечения прямой $HF$ с прямой $AA′$ , получаем $KA ′ = 37AA′$ . Стало быть, $A ′K :KA = 3:4.$

Ответ:

$3 :4$

Ошибка.
Попробуйте повторить позже

Задача 9#91453

В пирамиде $ABCD$ проведено сечение $KMLN$ так, что точка $K$ лежит на ребре $AD,$ точка $M$ — на ребре $DC,$ точка $N$ — на ребре $AB,$ точка $L$ на ребре $BC,$ и $O$ — точка пересечения диагоналей $KL$ и $MN$ четырехугольника $KMLN.$ Сечение $KMLN$ делит пирамиду на две части. Найти отношение объемов этих частей, если известны следующие соотношения между длинами отрезков:

4⋅OL = 3⋅OK,25⋅ON = 24⋅OM,DK ⋅NA − KA ⋅BN = KA ⋅NA.

Источники: Вступительные на ВМК МГУ - 1987 (pk.cs.msu.ru)

Показать ответ и решение

$PIC$

Запишем теорему Менелая для треугольника $KLP$ и секущей $MN$ :

KO-⋅ LN-⋅ P-M-= 1⇐⇒ 4⋅ LN-⋅ PM-= 1 (1) OL NP MK 3 NP MK

Пусть $NLLP-=a, PMMK =b$ . Тогда

P-K-= PM-+-MK--= PM-+ 1= b+ 1 и LN-=--LN--- = -a-- (2) KM KM MK NP LN + LP a+1

Подставив найденные значения отношений, получим систему

{ -a-⋅b= 3 aa+(b1+1)=424 , 25

которая легко решается: $a =3∕25,b =7$ . Пишем теорему Менелая для треугольника $AKP$ и прямой $DC$ :

PM-⋅ KD ⋅ AC-= 1⇔ KD ⋅ AC-= 1 (3) MK DA CP DA CP 7

А теперь - теорему Менелая для треугольника $ANP$ и прямой $BC$ :

NL- PC- AB- P-C -AB 25 LP ⋅CA ⋅BN =1 ⇐⇒ CA ⋅BN = 3 (4)

Перемножим равенства (3) и (4):

KD AB 25 DA-⋅BN- = 21 (5)

Соотношение $DK ⋅NA − KA ⋅BN =KA ⋅NA$ , данное в условии, можно переписать в виде $DKKA-− BNNA-= 1$ .

Пусть $DKKA-= x,BNNA-= y$ . Тогда

KD- = -x--и AB-= 1 +1 DA x+ 1 BN y

Подставляя в (5) найденные значения отношений, получаем систему

{ x − y =1 x+x1-⋅ y+y1= 2251

из которой находим, что $y = 32,x = 52$ . Итак, $DKKA-= 52$ и $BNNA-= 32$ . Тогда $ABBN-= ANNB-+1 = 53$ . Подставив это значение $ANBB-$ в (4), найдем, что $PCCA-=5$ и $CPPA-= 56$ .