Цилиндр

Используя скалярное произведение, легко показать, что косинус угла между главной диагональю (осью луча) и любым ребром куба равен . Такое же значение имеет косинус угла между осью луча и нормалью к любой грани куба.

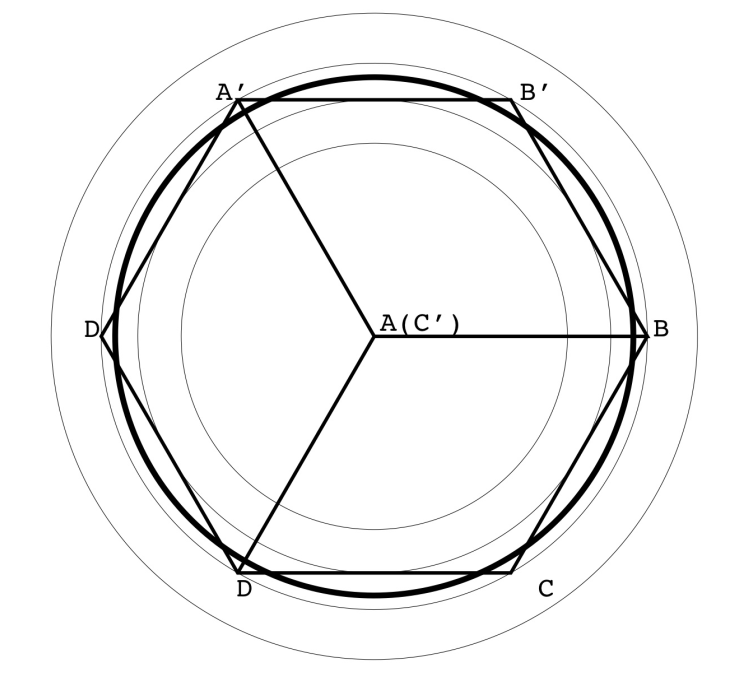
Изобразим проекцию куба на плоскость, перпендикулярную оси луча. Площадь проекции на эту плоскость любой плоской фигуры, расположенной на какой-либо грани куба, равна площади самой фигуры, умноженной на косинус угла между гранью и плоскостью проекции, т. е. на . Поэтому, вычислив площадь проекции освещённого участка куба и умножив её на , мы получим требуемый ответ.

Длина проекции любого ребра равна произведению длины ребра на косинус угла между ребром и плоскостью проекции или на синус угла между реброми осью луча, т. е. В случае, когда радиус луча не превышает радиуса вписанного в изображённый правильный шестиугольник окружности, проекция освещённого участка имеет площадь, равную Радиус вписанной в шестиугольник окружности равен Таким образом, при площадь освёщенного участка равна Если радиус больше или равен радиусу описанной около шестиугольника окружности, то полностью освещены три грани куба, т. е. при площадь освещенного участка равна Рассмотрим случай Площадь проекции освещённого участка получается вычитанием из шести площадей сегментов, вылезающих за шестиугольник. Площадь каждого такого сегмента равна разности площадей соответствующих сектора и треугольника. Угол сектора равен Поэтому площадь сегмента равна

где а площадь освещённого участка равна

Отметим, что соотношение равносильно неравенству определяющему -й рассматриваемый случай. По условию имеем имеем