Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
Основанием пирамиды является ромб
Высота пирамиды
равна 1, точка
лежит на прямой, содержащей
диагональ основания
причем
Боковое ребро
равно
а боковые грани наклонены к плоскости основания
под углами
и
Найдите длину стороны основания и угол между боковым ребром
и плоскостью боковой грани
Источники:
Подсказка 1
Чтобы найти сторону основания, нужно собрать про него побольше информации. Нам даны углы наклона боковых плоскостей к основанию, а также длина высоты. С помощью этого можно найти длины некоторых отрезков в основании, используя теорему о трёх перпендикулярах.
Подсказка 2
Проведите перпендикуляр из K к прямым AB и DC. Обозначьте точки пересечения с ними M и N. Как раз там и будут углы между боковыми плоскостями и основанием. Теперь вы можете легко посчитать KM, KN, CK. А дальше небольшой счёт в ромбе даст вам длину стороны.
Подсказка 3
Давайте теперь построим угол между TA и TCD. Для этого нам нужен перпендикуляр из точки A на плоскость TCD. Пусть FA || TK и F лежит на TC, а AL || DC и L лежит на MC. Может поискать его в плоскости AFL?
Обозначим точки пересечения прямых и
с перпендикуляром из точки
к этим прямым за
и
соответственно.
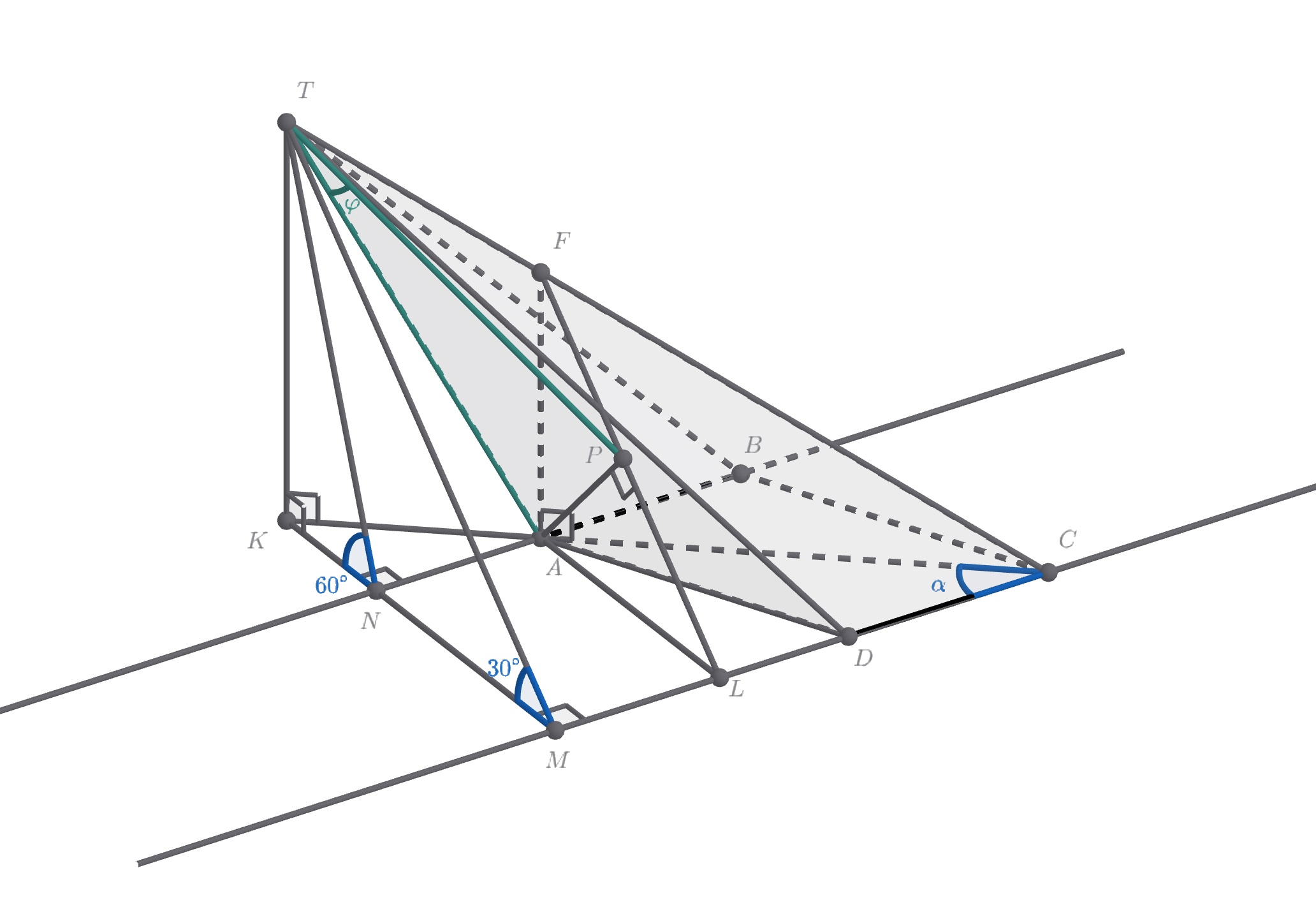
Тогда, так как угол и
— перпендикуляр к плоскости основания, получаем. что
Аналогично для угла
Так как треугольник прямоугольный с гипотенузой
то по теореме Пифагора
Аналогично для треугольника
Пусть тогда
По формуле синуса двойного угла получим
Тогда сторона основания равна
Откуда получаем
Так как то
Проведем так как
то
откуда получим
Построим перпендикуляр Так как
— прямоугольник, то
Из прямоугольного треугольника получаем
Построим — проекция
на плоскость
угол
— искомый угол.
тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




