Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
Сфера проходит через вершины
и
и середины рёбер
и
тетраэдра
Высота тетраэдра, опущенная из
точки
имеет длину
а радиус описанной окружности треугольника
составляет
Найдите радиус сферы
Источники:
Подсказка 1
С первого взгляда непонятно, а что это вообще за сфера? Давайте подумаем, как она связана с пирамидой. Например, что является пересечением сферы и треугольников ABC, A₁B₁C₁?
Подсказка 2
Верно, это описанные окружности этих треугольников! А как относятся друг к другу центры этих окружностей и центр сферы?
Подсказка 3
Они лежат на одиной прямой! Пусть R — искомый радиус, а x — расстояние между центром одной из окружностей и центром сферы. Попробуйте связать эти значения, расписав какую-нибудь теорему.
Подсказка 4
Если O', O и O₁ — центры сферы и окружностей, описанных около ABC и A₁B₁C₁ соответственно, то треугольники O'O₁A и O'OA — прямоугольные. Распишите для них теорему Пифагора) Не забудьте рассмотреть случай разного расположения точек O', O и O₁ относительно друг друга на прямой!
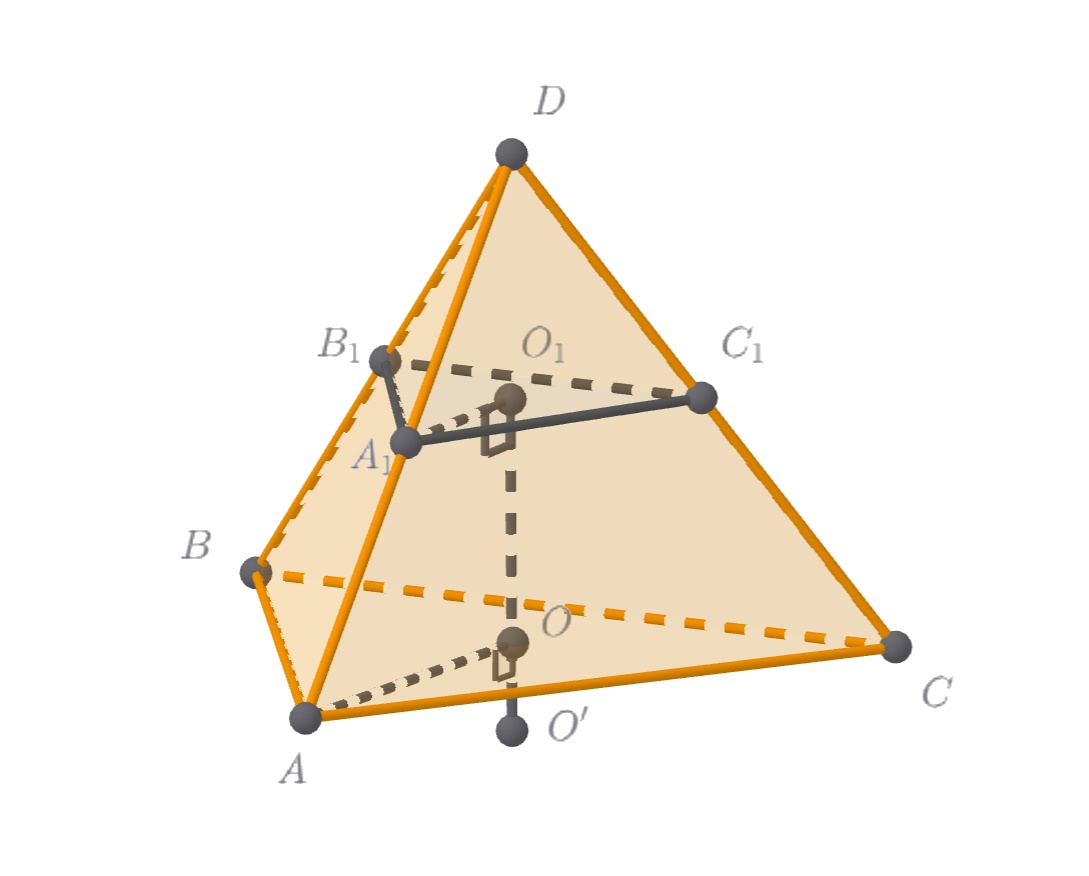
Заметим, что треугольник, образованный указанными серединами рёбер (назовём его подобен треугольнику
с
коэффициентом
Значит, и радиус его описанной окружности в два раза меньше, и составляет
Центры описанных окружностей этих треугольников назовём и
соответственно, центр сферы назовём
Плоскости
и
параллельны, и их пересечения со сферой — это описанные окружности треугольников, поэтому точки
и
лежат на
одной прямой, перпендикулярной этим плоскостям. Значит,
(расстояние между плоскостями, равное половине высоты
тетраэдра).
Пусть — искомый радиус сферы,
где
будем считать отрицательным, если точка
лежит по ту же сторону, что и
Тогда из теоремы Пифагора для треугольников
и
получим следующие равенства:
Приравняв их правые части, раскрыв скобки и сократив получаем
Отсюда
Теперь подставив в равенство
найдём
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




