Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
В каком отношении точка
делит сторону
основания правильной четырехугольной пирамиды
боковое ребро которой наклонено к основанию под углом
если известно, что площадь треугольника
минимально
возможная?
Источники:
Подсказка 1
Введем обозначения: сторона основания равна a, ∠SBO = β, OM ⊥ BE, ∠CBE = α (это будет переменная величина), ∠EBD = 45° - α, высота пирамиды SO = H, ∠SMO = γ. Попробуйте выразить рёбра.
Подсказка 2
Заметим, что BO = a/√2, OM = a ⋅ sin(45° - α)/√2, BE = a/cos(α). Посмотрим на треугольник SBE. Какие способы нахождения площади в пространстве Вы знаете?
Подсказка 3
Например, отношение площади и ее проекции можно связать с углом наклона.
Подсказка 4
Вычислим площадь треугольника SBE через площадь треугольника BOE, являющегося его проекцией, и cos(γ).
Подсказка 5
Площадь должна быть наименьшей. Возьмите производную и определите, каким условиям должна удовлетворять точка минимума.
Подсказка 6
cos не обращается в 0 на отрезке [0;π/4]. Какому условию тогда должна удовлетворять точка экстремума?
Подсказка 7
Единственный экстремум — это точка a', для которой tg(a') = a² / (4H² + a²). Точкой минимума или максимума будет являться a'?
Подсказка 8
Заметим, что f'(0) = -a² < 0 и f'(π/4) = 8H² > 0, следовательно, a' является точкой минимума. Теперь попробуйте выразить H через угол β.
Подсказка 9
H = arctg(β) / √2, подставьте это в условие для экстремума.
Подсказка 10
CE:CD = CE:BC, а это в точности tg(a').
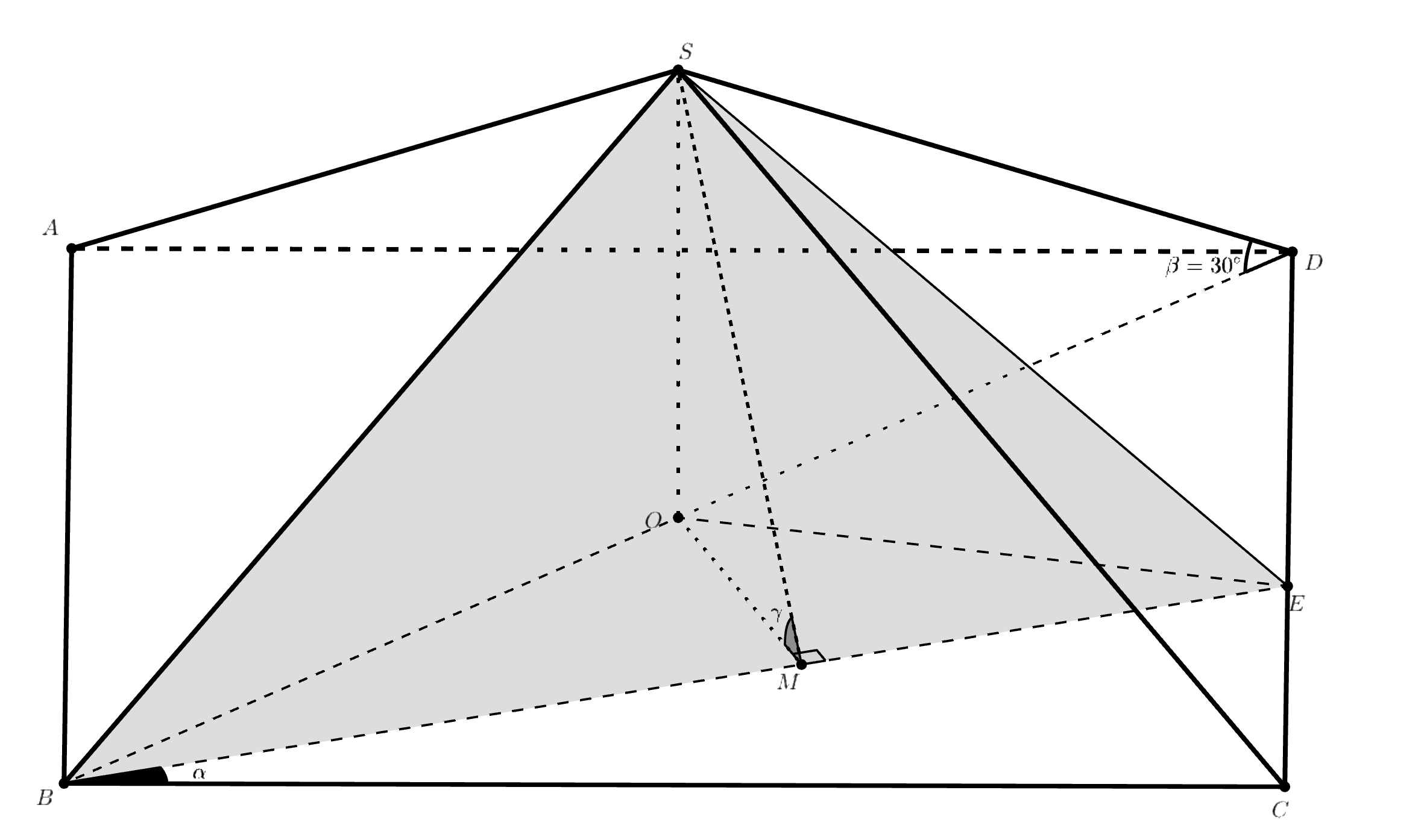
Введем обозначения: сторона основания равна
(переменная величина),
высота
пирамиды
Тогда
Найдем площадь проекции сечения
Вычислим угол наклона сечения
Тогда
Преобразуем полученное выражение:
Наименьшее значение площади соответствует значению
при котором
достигает минимума, где
Найдем экстремумы
На отрезке косинус не обращается в 0, поэтому единственным экстремумом будет точка
для которой
Так как
является точкой минимума.
С учетом того, что
получаем
Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




