Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
Высота правильной треугольной призмы с основанием
и боковыми рёбрами
равна
Найдите длину
ребра основания, если известно, что
Источники:
Подсказка 1
Как мы можем применить данную нам перпендикулярность? Кажется, будет удобно построить из точки B' прямую B'B₁, параллельную BC' и взглянуть, на полученную конструкцию. Обозначьте неизвестную сторону основания какой-нибудь переменной и попробуйте выразить всё что тут можно!
Подсказка 2
В основании правильный треугольник, значит у нас есть угол в 60°. Имея в треугольнике две стороны и угол мы сумеем выразить третью сторону: отрезок, соединяющий А с точкой пересечения B'B₁ и плоскости основания. Эту же сторону мы можем выразить при помощи т. Пифагора.
Подсказка 3
Осталось только решить квадратное уравнение, отсечь лишний корень (сторона ведь не может быть отрицательной!) и задача повержена!
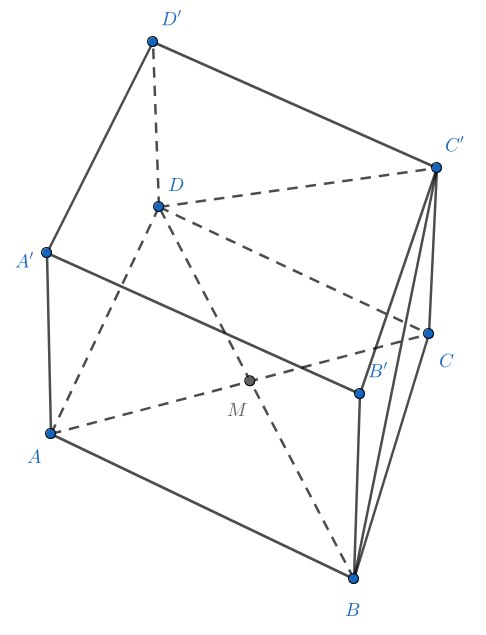
Достроим основания призмы до параллелограммов, получим
. Получится параллелепипед, в котором
и
, отсюда
. Кроме того,
(призма правильная, можно воспользоваться
симметрией. Отсюда
прямоугольный и равнобедренный. Если
, то
будет высотой этого треугольника, если
дополнительно
, то
(используем свойства правильного треугольника). Из условия
, применяя теорему Пифагора:
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




