Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
Точка — начало трех отрезков
и
лежащих в плоскости
и имеющих длины 3,4 и 7 соответственно. На прямой
,
проходящей через точку
и перпендикулярной плоскости
, расположена точка
так, что сумма углов, образуемых прямыми
и
с прямой
, равна
. Найти длину отрезка
.
Источники:
Подсказка 1
Треугольники ODA, ODB и ODC прямоугольные, также они имеют общую сторону OD. Если её обозначить за переменную, как можно будет записать условие на сумму трёх углов?
Подсказка 2
Пусть OD = x, тогда углы выражаются через арктангенсы. Тогда из условия получаем, что сумма трёх арктангенсов равна π. Что же хочется сделать? Взять от обеих частей тангенс! Но для тангенса суммы двух углов мы формулу знаем, чего не скажешь о суммы трёх. А вот π одиноко стоит с правой стороны, тогда можно сначала перенести одно слагаемое на правую часть и потом уже делать махинации со взятием тангенса.
Подсказка 3
Тогда взяв тангенс от обеих частей (но помните, что нужно будет сделать проверку равносильности такого перехода!) и применив формулу тангенса суммы, получаем совсем простое квадратное уравнение для x.
Обозначим через
.
![]()
Из прямоугольных треугольников выражаем углы
По условию нам дано
Преобразуем
Возьмём тангенс от обеих частей (проверку равносильности такого перехода отложим) и применим формулу тангенса суммы
поэтому подходит только
.
Теперь вернёмся к уравнению до взятия тангенсов и подставим туда этот корень. Правая часть лежит на отрезке
Левая тоже, потому что оба арктангенса по определению положительные и меньше
То есть они не могут отличаться на кратное
Так
что раз тангенсы получились равны, то и сами углы равны.
Ошибка.
Попробуйте повторить позже
В пирамиде с вершиной
известно, что
5 и
. Найдите длину ребра
, если вписанная в пирамиду
сфера касается основания в точке пересечения диагоналей четырёхугольника
.
Источники:
Подсказка 1
Сфера даёт очень много точек касания, а значит, очень много равных отрезков касательных. Попробуйте найти пары равных треугольников (их точно больше 5).
Подсказка 2
Вы получили очень много равных углов, но отдельных равенств недостаточно, тогда как бы их объединить? Вспомните, чему равна сумма углов вокруг точки, и посчитайте такие суммы для точек касания сферы боковых сторон.
Подсказка 3
Из полученных равенств попробуйте найти угол между диагоналями основания. Это знание и поможет посчитать искомую сторону:)
Обозначим точки касания сферы с гранью основания и гранями и
буквами
и
соответственно.
По свойству отрезков касательных, соответствующие отрезки касательных к сфере будут равны. Значит, по признаку равенства по трём сторонам будут равны треугольники
а также
Следовательно, будут равны все соответствующие углы этих треугольников.
![]()
Поскольку вертикальные углы между диагоналями равны, то будут равны углы
и
.
Рассматривая суммы углов вокруг точек
и
получаем, что все углы равны:
Так как эти же углы получаются между диагоналями в основании и образуют вокруг точки
в сумме
, то углы прямые
и диагонали
и
перпендикулярны.
Обозначим длины отрезков и
за
и
соответственно. Применяя теорему Пифагора для треугольников
и
получим равенства:
Складывая первое и третье и вычитая второе равенство, получим
. Из теоремы Пифагора для
треугольника
находим отрезок
.
Ошибка.
Попробуйте повторить позже
Найдите синус угла между высотами, опущенными из двух вершин правильного тетраэдра на противоположные грани.
Пусть дан правильный тетраэдр со стороной
в котором проведены высоты
и
пересекающиеся в точки
Отметим
середину
как
и проведём медианы
и

В силу того, что тетраэдр правильный, точки и
будут является центрами соответствующих граней, а значит будут лежать на
и
соответственно. Заметим, что четырёхугольник
вписанный по двух двух прямым противолежащим
углам, следовательно,
поэтому
Так как
и
— медианы в
правильных треугольниках, они равны
Сделаем выносной чертёж треугольника
проведя его медиану
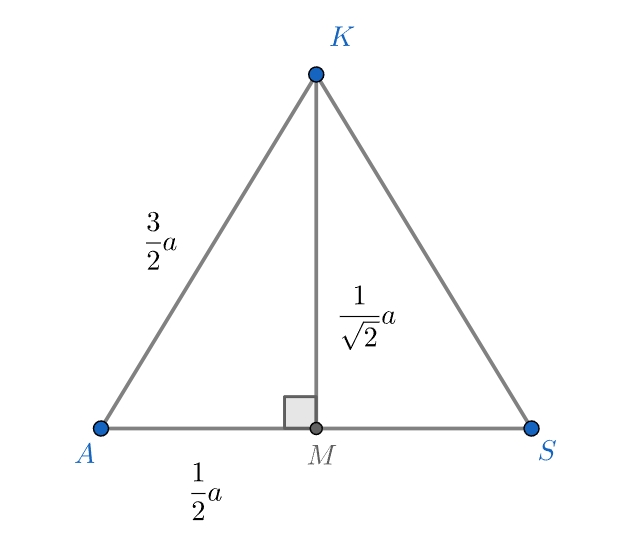
Так как треугольник равнобедренный, то
является биссектрисой и высотой, поэтому
По теореме Пифагора поэтому
В итоге получаем, что
Ошибка.
Попробуйте повторить позже
Для монтажа бурового оборудования в скважину используется подвес, состоящий из металлического каркаса в форме равностороннего
треугольника и трёх регулируемых по длине тросов протянутых через вершины треугольника и соединяющихся на крюке. Расстояние
между тросами на каркасе составляет м, а их первоначальная длина от каркаса до крюка —
м. При спуске оборудования оказалось,
что крюк нужно сместить на
м вдоль медианы каркаса по направлению от вершины. На сколько метров нужно удлинить трос,
проходящий через эту вершину?
Источники:
Подсказка 1
Из условия следует, что у нас изначально есть правильный тетраэдр со стороной 2. После этого мы как-то меняем положение крюка, чтобы точка вершины сдвинулась вдоль медианы в основании на нужную длину. Подумайте, что это значит в терминах геометрии.
Подсказка 2
Это значит, что проекция вершины S на плоскость основания сместилась на нужную длину, но при этом проекция S всё равно лежит на медиане. Если S₁ — новая точка, то мы можем посчитать S₁O₁ как катет прямоугольного треугольника S₁DO₁, где D — середина BC, а O₁ — сдвинутая на нужную длину точка O. Но тогда мы можем найти и S₁A (из какого прямоугольного треугольника?), а значит, и разность длин троса. Ну и всё, идейно задача решена, осталось посчитать!
Пирамида — правильная, тогда медиана
а апофема
Так как — точка пересечения медиан треугольника
, то
При увеличении длины троса проекция вершины пирамиды переместиться в точку
, так что
, тогда
Поскольку, при увеличении длины троса до
длина апофемы треугольника
равна
, то
Следовательно,
Тогда трос нужно удлинить на .
Ошибка.
Попробуйте повторить позже
В правильной треугольной пирамиде дана сторона основания и высота
. Найти длину бокового ребра.
Подсказка 1
По условию нам дана длина высоты и сказано, что пирамида правильная. Давайте проведем эту высоту, тогда в какую точку на основании пирамиды она упадет?
Подсказка 2
Если опустить высоту в правильной пирамиде, то основание высоты совпадёт с центром основания пирамиды.
Подсказка 3
По условию нам дана длина стороны основания, значит, мы можем найти радиус описанной окружности около основания, следовательно, можем найти боковую сторону пирамиды по теореме Пифагора.
.png)
Пусть это пирамида ,
— центр основание. Поскольку основание является правильным треугольником, то
, а
также
, отсюда легко найти
.
Ошибка.
Попробуйте повторить позже
Одна из высот некоторого тетраэдра проходит через точку пересечения высот противоположной грани. Докажите, что все остальные высоты тетраэдра обладают этим же свойством.
Подсказка 1
Нам нужно получить, что все высоты обладают этим свойством. Может, надо найти какие-то связи между ребрами тетраэдра...
Подсказка 2
Пускай для определенности именно высота DH обладает этим свойством. Тогда H- ортоцентр треугольника ABC. На картинке много прямых углов, пора использовать теорему о трех перпендикулярах!
Подсказка 3
Но применять ее нужно хитро: попробуйте провести через точку A прямую, параллельную BC, и использовать нашу любимую теорему!
Подсказка 4
Получается, что AD перпендикулярна прямой, параллельной BC. Но тогда AD перпендикулярна BC. Это мы выяснили, поработав только с точкой A. Может, нужно поработать с точками B и C...
Подсказка 5
Аналогично рассуждая, можно прийти к тому, что BD перпендикулярна AC и CD перпендикулярна AB. Получается, что скрещивающиеся ребра попарно перпендикулярны. Попробуйте теперь провести высоту AN и доказать, что N- ортоцентр BCD.
Подсказка 6
Достаточно доказать, что BN- отрезок высоты треугольника BCD. Попробуйте провести похожие рассуждения с 3 подсказкой, только с обратной теоремой о трех перпендикулярах, и будет вам счастье!
.png)
Пусть это тетраэдр и
— данная в условии высота, откуда
.
Проведём . Используя теорему о трёх перпендикулярах для
, имеем
. Аналогично в силу симметрии можно заключить
. Мы доказали попарную
перпендикулярность противоположных рёбер тетраэдра.
Рассмотрим теперь высоту и проведём
Поскольку
, то по обратной теореме о трёх
перпендикулярах
или
. Значит,
лежит на высоте грани из вершины
. Аналогично показываем, что она
лежит и на других высотах, откуда и получаем требуемое.
Ошибка.
Попробуйте повторить позже
Объём правильной треугольной пирамиды равен одной шестой куба бокового ребра. Найдите плоский угол при вершине.
Подсказка 1
Наверное, вся сложность этой задачи состоит в том, как искать плоский угол. Может попробовать найти его половинку, ведь для этого всего-то надо найти отношение бокового ребра к ребру основания...
Подсказка 2
Пускай ребро основания равно a, боковое ребро- x. Попробуйте расписать объём пирамиды через a и x, тогда мы найдем связь между ними (не забудьте, что по условию объем также равен x³/6)
Подсказка 3
Приравняв объем, выраженный через a и x, к x³/6, можно поделить обе части на a³ и сделать замену t=x/a. Осталось только решить иррациональное уравнение...
Подсказка 4
Можно возвести обе части в квадрат и сделать замену s=t². Подберите корень в кубическом уравнении (подставьте например 1 или -1...) и доведите решение до конца!
Первое решение.
![]()
Так как
то
|
|
Решая данную систему, получаем:
________________________________________________________________________________________
Второе решение. Пусть ребро основания равно , а боковое —
.
.png)
Тогда объём пирамиды можно посчитать по формуле (высоту легко найти из теоремы Пифагора)
Мы составили уравнение, остаётся понять, что искать. Оказывается, нам достаточно найти , проще говоря,
достаточно найти значение
. Зная это, преобразуем уравнение, сделав замену
(для этого поделим обе части на
)
После замены получаем
Сразу несложно увидеть решение Вынося его, получим
Получаем или
откуда
Подойдёт только
, откуда
, значит,
.
Ошибка.
Попробуйте повторить позже
Подсказка 1
Часто, чтобы доказать в стереометрии, что какие-то две прямые перпендикулярны, нужно найти такую плоскость, для которой одна из прямых содержится в этой плоскости, а другая перпендикулярна этой плоскости. Попробуйте сделать то же самое в этой задаче для прямых A₁C₁ и C₁B.
Подсказка 2
Да, во-первых, A₁C₁ перпендикулярна C₁B₁, так как треугольник A₁B₁C₁-прямоугольный, а во-вторых, A₁C₁ перпендикулярна C₁C, в силу того, что перед нами призма. Значит, A₁C₁ перпендикулярна всей плоскости C₁CB. Значит, и прямой C₁B. Также, мы знаем два отрезка в треугольнике A₁C₁B , и знаем, что он прямоугольный. Кажется, теперь задача превратилась в счетную, где можно найти все отрезки(ведь тут одни прямоугольные треугольники). Осталось посчитать!
![]()
Поскольку (
и
), то, в частности,
. По теореме Пифагора для
имеем
. А по той же теореме для
получим
и для
. Теперь мы готовы считать
объём
Ошибка.
Попробуйте повторить позже
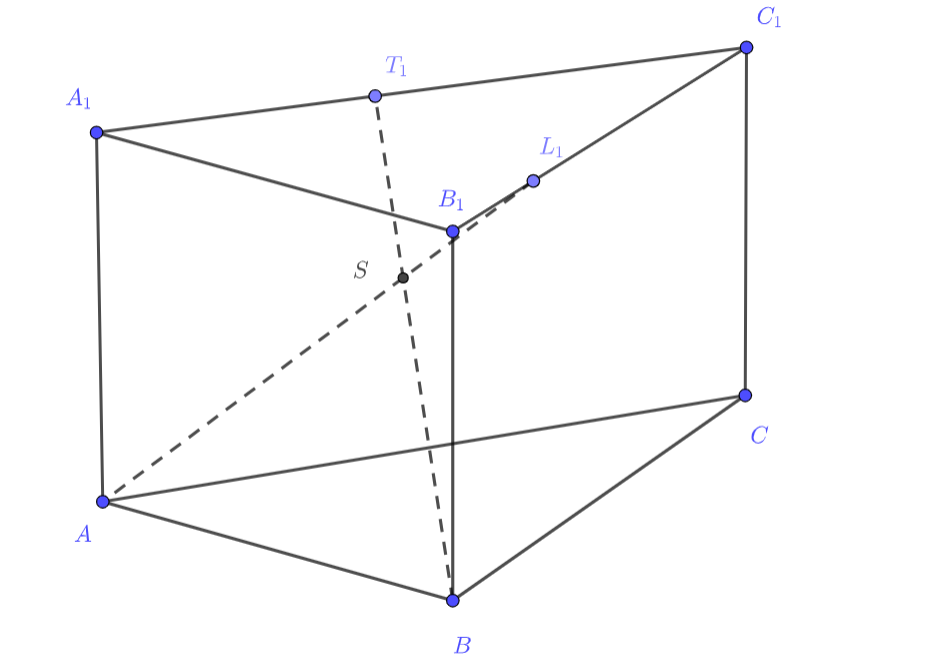
Высота правильной треугольной призмы с основанием
и боковыми рёбрами
равна
Найдите длину
ребра основания, если известно, что
Источники:
Подсказка 1
Как мы можем применить данную нам перпендикулярность? Кажется, будет удобно построить из точки B' прямую B'B₁, параллельную BC' и взглянуть, на полученную конструкцию. Обозначьте неизвестную сторону основания какой-нибудь переменной и попробуйте выразить всё что тут можно!
Подсказка 2
В основании правильный треугольник, значит у нас есть угол в 60°. Имея в треугольнике две стороны и угол мы сумеем выразить третью сторону: отрезок, соединяющий А с точкой пересечения B'B₁ и плоскости основания. Эту же сторону мы можем выразить при помощи т. Пифагора.
Подсказка 3
Осталось только решить квадратное уравнение, отсечь лишний корень (сторона ведь не может быть отрицательной!) и задача повержена!
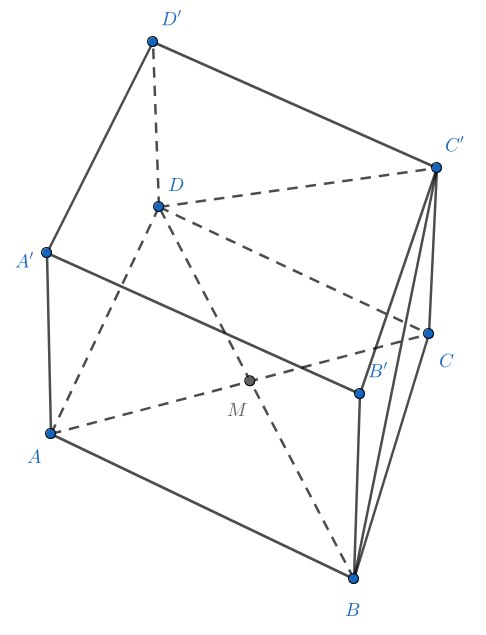
Достроим основания призмы до параллелограммов, получим
. Получится параллелепипед, в котором
и
, отсюда
. Кроме того,
(призма правильная, можно воспользоваться
симметрией. Отсюда
прямоугольный и равнобедренный. Если
, то
будет высотой этого треугольника, если
дополнительно
, то
(используем свойства правильного треугольника). Из условия
, применяя теорему Пифагора:
.
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида с основанием
и вершиной
Плоскость
перпендикулярна ребру
и
пересекает рёбра
в точках
соответственно. Известно, что
и
Найдите косинус угла между ребром
и плоскостью основания
Источники:
Подсказка 1
Пирамида правильная, поэтому мы чётко знаем куда падает её высота и искомый косинус будет легко выражаться, как только мы узнаем отношение её бокового ребра к ребру основания. Плоскость π перпендикулярна AS. Что в таком случае можно сказать о прямой DE пересечения этой плоскости с плоскостью (SAB)?
Подсказка 2
Итак, DE ⊥ AS. Тогда мы можем, зная положения точек D и E выразить косинус угла при вершине S. Рассмотрите теперь равнобедренный треугольник-грань △ASB: теорема косинусов поможет нам связать его боковые стороны со стороной основания.
Подсказка 3
Пирамида правильная, значит её высота падает в центр основания. Воспользуйтесь свойствами правильного треугольника и найденным в предыдущем пункте соотношением, чтобы выразить искомый косинус.
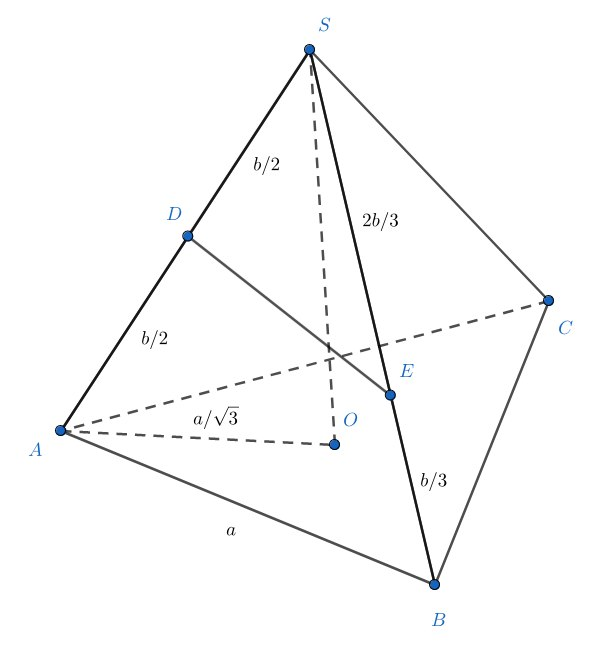
Пусть — длина ребра основания и
— длина бокового ребра. В прямоугольном треугольнике
имеем
и
. Стало
быть,
. Применяя теорему косинусов к треугольнику
, получаем, что
, откуда
. Пусть
— центр основания. Тогда в прямоугольном треугольнике
имеем
и
. Стало быть,
.
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде отметили середину
медианы
треугольника
. Оказалось, что эта точка
удалена от прямых
и от грани
на расстояние 1 . Найдите объём параллелепипеда.
Источники:
Подсказка 1
Давайте для начала попробуем изучить картинку. Наша точка O равноудалена от прямых AD' и AB', следовательно она лежит на биссектрисе угла ∠D'AB'. Но по условию, O- середина медианы. Что мы тогда можем сказать про треугольник △D'AB'?
Подсказка 2
Верно, он равнобедренный! Тогда AD'=AB'. Значит и прямоугольные треугольники △AA'B' и △AA'D' равны по катету и гипотенузе. Нетрудно видеть, что расстояние от M до плоскости (ABCD) равно удвоенному расстоянию от O до этой же плоскости, т.е. 2. Давайте обозначим длину AB за x и попробуем выразить через нее остальные отрезки...
Подсказка 3
AB' и B'D' можно легко найти из теорем Пифагора. Тогда в треугольнике △D'AB' мы знаем все стороны ⇒ можем воспользоваться формулой для нахождения медианы AM. А что можно сказать про треугольники △AOX и △AB'M?
Подсказка 4
Точно, они подобны! Тогда B'M*AO/AB' = OX = 1, где X- основание перпендикуляра из O на AB'. Мы уже умеем выражать B'M, AO и AB' через x, поэтому мы сможем решить уравнение и найти x. Сделайте это и завершите решение!
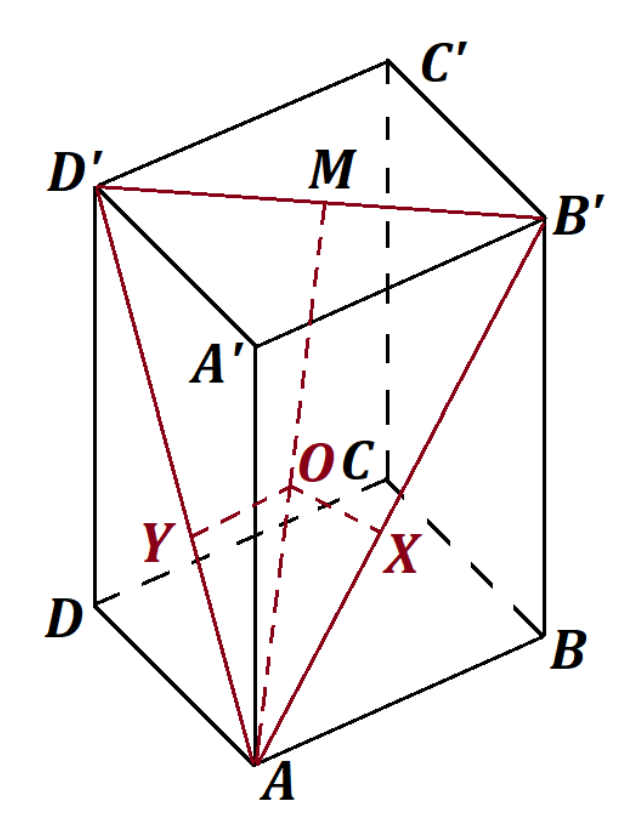
Пусть и
- это основания перпендикуляров, опущенных из
на
и
. Точка
на медиане
равноудалена от
сторон треугольника
, поэтому она лежит также на биссектрисе; значит, медиана является биссектрисой, поэтому
по катету и гипотенузе, тогда
Обозначим длины отрезков
и
через
и
.
Тогда
. Taкжe
Расстояние от точки до основания
в 2 раза меньше, чем расстояние от
до основания
то есть
,
откуда легко получается
и
то есть . Объём равен
.
Ошибка.
Попробуйте повторить позже
Точка лежит на ребре
куба
В квадрат
вписан прямоугольник
так, что одной из его вершин
является точка
а три другие расположены на различных сторонах квадрата основания. Прямоугольник
является
ортогональной проекцией прямоугольника
на плоскость верхнего основания
Диагонали четырехугольника
перпендикулярны. Найти отношение
Источники:
Подсказка 1
Давайте ещё рассмотрим четырёхугольник MK₁L₁N. Что мы можем сказать о параллельности его сторон, углах; в целом, какого рода этот четырёхугольник?
Подсказка 2
Так как его стороны MN и L₁K₁ равны и параллельны, то MK₁L₁N — параллелограмм. Также рассмотрим его углы, воспользовавшись теоремой о трёх перпендикулярах. И о чём в таком случае говорит перпендикулярность диагоналей?..
Подсказка 3
Правильно, MK₁L₁N — квадрат. Обозначим сторону куба за а. Тогда можно выразить из AB отрезки AM и MB (пусть один из отрезков равен λa, где λ - некоторая неизвестная). Теперь, чтобы найти отношение АМ:МВ, нам достаточно просто найти λ.
Подсказка 4
MK₁ и MN равны как стороны квадрата MK₁L₁N и к тому же легко выражаются через длины АМ и МВ с помощью нескольких теорем Пифагора. Осталось только верно выразить эти стороны через λ и а и приравнять, сократив а. И не забудьте, что главный вопрос задачи — найти отношение, а не λ!
и
, поэтому четырехугольник
— параллелограмм. По теореме о трёх перпендикулярах угол
прямой, поэтому
— прямоугольник. Его диагонали по условию перпендикулярны, поэтому
—
квадрат.
Пусть — ребро куба,
с неизвестным
![]()
Тогда и по теореме Пифагора
Стороны и
равны, поэтому
В итоге
так что
Ошибка.
Попробуйте повторить позже
Треугольник со сторонами ,
,
является основанием прямой призмы
. Боковое ребро призмы равно 2.
Найдите расстояние от точки
до прямой
.
Заметим, что по теореме о трех перпендикулярах можно либо сразу опустить перпендикуляр на прямую
, либо сначала
опустить перпендикуляр
на плоскость
, а затем опустить перпендикуляр
на прямую
. Точку
найти легко, так
как призма прямая, и значит,
.
![]()
Тогда лежит в плоскости
и является высотой в треугольнике
. Так как треугольник
равнобедренный,
то
еще и медиана, а значит,
— середина
и
.
Теперь нужно посчитать . Так как
, то треугольники
и
подобны.
Значит,
Тогда так как , то
и значит,
Ошибка.
Попробуйте повторить позже
Пусть и
– площади граней произвольного тетраэдра, прилегающих к ребру
– двугранный угол при этом ребре;
– ребро,
противоположное
– угол между ребрами
и
. Докажите, что верна формула
Пусть нам дан тетраэдр , у которого
и
. Проведем прямую параллельную
через
и
выберем на ней точку
такую, что
параллелограмм. Опустим перпендикуляр
в треугольнике
, высоту
в
тетраэдре и перпендикуляр
в параллелограмме
. Тогда
по параллельности и по теореме о трех
перпендикулярах
. Значит, точки
и
лежат на одной прямой. Тогда опять по теореме о трех перпендикулярах, так
как
, то
высота в треугольнике
.
![]()
Мы знаем, что — двугранный угол при ребре
. Значит,
. Мы знаем, что
— угол между ребрами
и
. Значит,
.
Тогда по определению синуса . С другой стороны, по теореме косинусов
Заметим, что раз — высота в треугольнике
, то
. Так как
высота параллелограмма
, то это и
высота треугольника
. Значит,
. Отсюда
Ошибка.
Попробуйте повторить позже
Тетраэдр называется равногранным, если все его грани равны.
Замечание. Легко проверить, что тетраэдр равногранный тогда и только тогда, когда
В равногранном тетраэдре опущена высота
.
— точка пересечения высот грани
— длины отрезков, на
которые одна из высот грани
делится точкой
.
(a) докажите, что точки и
симметричны относительно центра описанной окружности треугольника
.
(b) докажите, что .
(a) Пусть — высота в треугольнике
— высота в треугольнике
— середина
и
— проекция
на
.
![]()
Заметим, что так как — высота тетраэдра и
высота в треугольнике
, то
. Мы знаем, что
— середина
, поэтому ее проекция
на
это середина
, так как
— проекция
, а
проекция
. Так как треугольники
и
равны, то равны и их соответствующие части, а именно
. Значит,
и поэтому
середина
. Аналогично остальные проекции
на стороны будут серединами. Значит,
— центр описанной
окружности.
(b) Пусть и
. Заметим, что
![]()
Из симметрии и
относительно центра описанной окружности
следует, что
И мы знаем, что
Тогда
Ошибка.
Попробуйте повторить позже
На рёбрах куба
отмечены точки
так, что
. Найдите угол
, если
сторона куба равна 3.
Источники:
Подсказка 1
В таких задачах не нужно ничего говорить, нужно просто написать свой счет отрезков в мексиканской шляпе… А вообще, да, видно, что все отрезки треугольника нашего считаются, так как, к примеру YD1 перпендикулярно A1D1, а значит работает теорема Пифагора, отрезок YD1 также легко ищется, тоже по теореме Пифагора. Попробуйте посчитать и понять, чему равны стороны XYZ.
Подсказка 2
Верно, XY^2 = XB^2 + BC^2 + CY^2 = 4 + 9 + 1. Аналогично, YZ^2 = 14 = XZ^2. Значит, наш треугольник равносторонний, а значит его углы мы точно знаем!
Покажем, что треугольник — равносторонний. Действительно,
Таким образом, и треугольник
— равносторонний, а значит, угол
.
![]()
Ошибка.
Попробуйте повторить позже
Две смежные боковые грани пирамиды, в основании которой лежит квадрат, перпендикулярны плоскости основания. Двугранный угол
между двумя другими боковыми гранями равен . Найдите отношение высоты пирамиды к стороне основания.
Источники:
![]()
Пусть это пирамида , где
(то есть основанию перпендикулярны
и
). Обозначим сторону квадрата из
основания за
.
В силу симметрии высоты и
к
пересекаются в одной точке. Тогда из условия
, как
угол между высотами к общей прямой двух плоскостей. Далее в силу той же симметрии
и
, то есть
и
. Отсюда
. Далее заметим, что
, поскольку
перпендикулярна двум прямым
и
, откуда
. Тогда
. Тогда
. Осталось
найти
То есть высота пирамиды равна стороне основания.
Ошибка.
Попробуйте повторить позже
(a) Точки и
лежат на окружности с диаметром
значит,
(т.е.
и
высоты
треугольника
Прямая
— это проекция прямой
на плоскость основания, при этом
Тогда по теореме
о трёх перпендикулярах
т.e.
(b) Поскольку прямые и
пересекаются, то все четыре точки
и
лежат в одной плоскости (назовём
её
). Значит, прямые
и
лежат в одной плоскости
а так как они не пересекаются (поскольку лежат в
параллельных друг другу основаниях призмы), то
Значит,
Трапеция
вписана в окружность,
следовательно, она равнобокая, тогда углы при её основании
равны, и поэтому треугольник
равнобедренный
Треугольники и
подобны по двум углам. Из равенства треугольников
и
следует,
что
поэтому оба треугольника
и
равнобедренные с основаниями
и
соответственно. Значит,
откуда
(c) Если то
;
. Значит, площадь
основания призмы равна
объём призмы равен
.



