Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная пирамида с основанием
и вершиной
Плоскость
перпендикулярна ребру
и
пересекает рёбра
в точках
соответственно. Известно, что
и
Найдите косинус угла между ребром
и плоскостью основания
Источники:
Подсказка 1
Пирамида правильная, поэтому мы чётко знаем куда падает её высота и искомый косинус будет легко выражаться, как только мы узнаем отношение её бокового ребра к ребру основания. Плоскость π перпендикулярна AS. Что в таком случае можно сказать о прямой DE пересечения этой плоскости с плоскостью (SAB)?
Подсказка 2
Итак, DE ⊥ AS. Тогда мы можем, зная положения точек D и E выразить косинус угла при вершине S. Рассмотрите теперь равнобедренный треугольник-грань △ASB: теорема косинусов поможет нам связать его боковые стороны со стороной основания.
Подсказка 3
Пирамида правильная, значит её высота падает в центр основания. Воспользуйтесь свойствами правильного треугольника и найденным в предыдущем пункте соотношением, чтобы выразить искомый косинус.
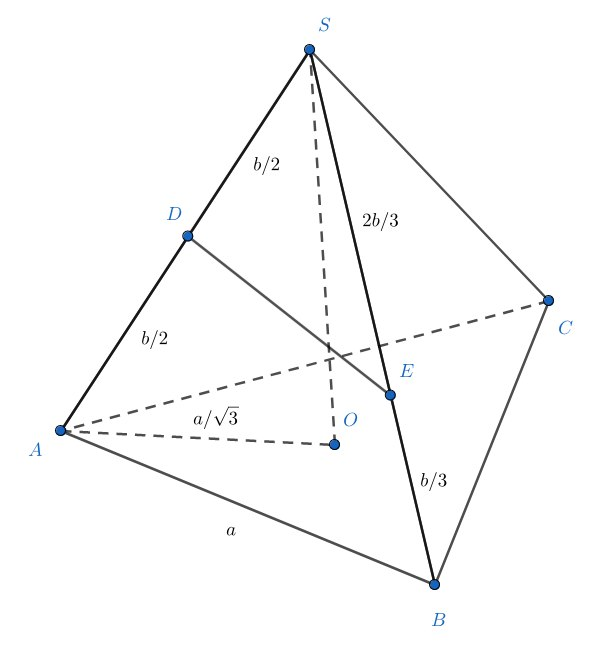
Пусть — длина ребра основания и
— длина бокового ребра. В прямоугольном треугольнике
имеем
и
. Стало
быть,
. Применяя теорему косинусов к треугольнику
, получаем, что
, откуда
. Пусть
— центр основания. Тогда в прямоугольном треугольнике
имеем
и
. Стало быть,
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




