Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде отметили середину
медианы
треугольника
. Оказалось, что эта точка
удалена от прямых
и от грани
на расстояние 1 . Найдите объём параллелепипеда.
Источники:
Подсказка 1
Давайте для начала попробуем изучить картинку. Наша точка O равноудалена от прямых AD' и AB', следовательно она лежит на биссектрисе угла ∠D'AB'. Но по условию, O- середина медианы. Что мы тогда можем сказать про треугольник △D'AB'?
Подсказка 2
Верно, он равнобедренный! Тогда AD'=AB'. Значит и прямоугольные треугольники △AA'B' и △AA'D' равны по катету и гипотенузе. Нетрудно видеть, что расстояние от M до плоскости (ABCD) равно удвоенному расстоянию от O до этой же плоскости, т.е. 2. Давайте обозначим длину AB за x и попробуем выразить через нее остальные отрезки...
Подсказка 3
AB' и B'D' можно легко найти из теорем Пифагора. Тогда в треугольнике △D'AB' мы знаем все стороны ⇒ можем воспользоваться формулой для нахождения медианы AM. А что можно сказать про треугольники △AOX и △AB'M?
Подсказка 4
Точно, они подобны! Тогда B'M*AO/AB' = OX = 1, где X- основание перпендикуляра из O на AB'. Мы уже умеем выражать B'M, AO и AB' через x, поэтому мы сможем решить уравнение и найти x. Сделайте это и завершите решение!
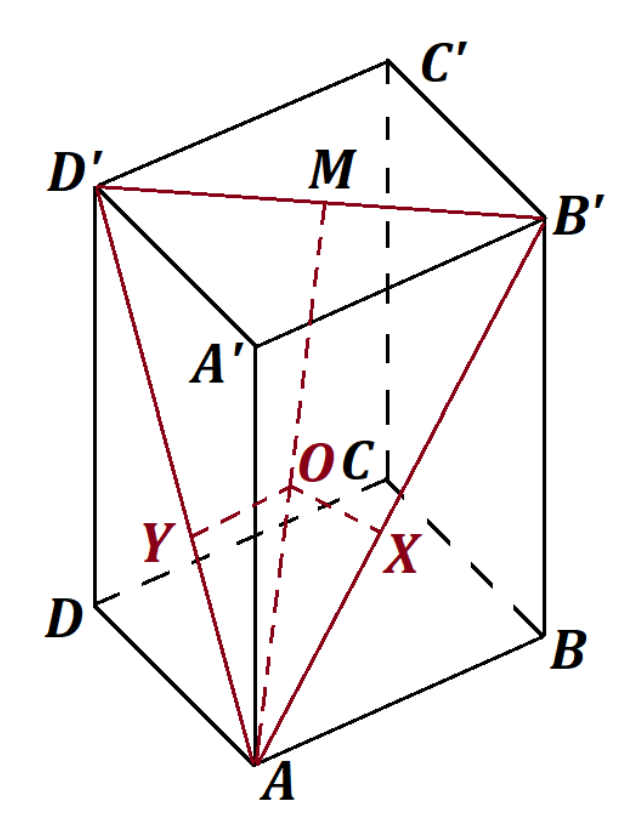
Пусть и
- это основания перпендикуляров, опущенных из
на
и
. Точка
на медиане
равноудалена от
сторон треугольника
, поэтому она лежит также на биссектрисе; значит, медиана является биссектрисой, поэтому
по катету и гипотенузе, тогда
Обозначим длины отрезков
и
через
и
.
Тогда
. Taкжe
Расстояние от точки до основания
в 2 раза меньше, чем расстояние от
до основания
то есть
,
откуда легко получается
и
то есть . Объём равен
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




