Пирамиды и призмы с общим основанием
Ошибка.
Попробуйте повторить позже
Докажите, что биссектор (плоскость, проходящая через ребро двугранного угла и делящая его на два равных двугранных угла) двугранного угла при ребре тетраэдра делит противоположное ребро на части, пропорциональные площадям тех граней тетраэдра, которые лежат на гранях этого двугранного угла.
Подсказка 1
Не правда ли, задача напоминает аналогичную в планиметрии с биссектрисой, только теперь вместо биссектрисы плоскость. Там мы доказывали это, выражая отношение площадей двумя способами и приравнивая их. А через что можно выразить нужные отношения в стереометрии?
Подсказка 2
Верно, можно сделать то же самое через объёмы тетраэдров, на которые разбивает биссектор исходный тетраэдр. Тогда выразим отношение объёмов через нужные площади и отрезки. Сначала давайте сделаем это для площадей, вспомнив, что мы ещё не пользовались равенством углов.
Подсказка 3
Ага, это равенство отношений мы получили. Теперь осталось получить его для отрезков. Давайте попробуем просто опустить высоты на общую грань тетраэдров. Чем тогда можно воспользоваться из планиметрии, чтобы связать высоты и отрезки грани?
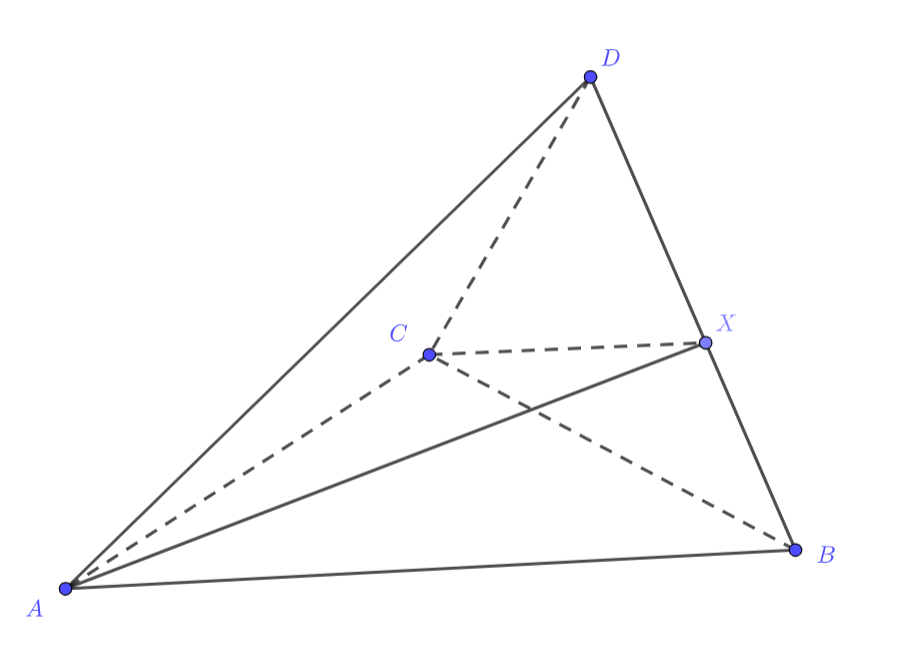
Пусть — высота треугольника
, а угол между плоскостями
и
равен
С одной стороны (расстояние от до грани по следствию из теоремы о трёх перпендикулярах падает на перпендикуляр, восставленный
из точки
в плоскости соответствующей грани):
С другой стороны (отношение расстояний до общей грани переписывается через отношение наклонных из подобия прямоугольных треугольников):
что и требовалось доказать
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




