Тема Счёт площадей и объёмов

Пирамиды и призмы с общим основанием

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела счёт площадей и объёмов

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80774

В основании призмы лежит равносторонний треугольник площади 1. Площади её боковых граней равны 3, 3 и 2. Найдите объём призмы.

Источники: Физтех - 2024, 11.7 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Во-первых, надо осознать картинку. Она, как будто, симметричная, но не стоит так думать сразу. Давайте опустим высоты из точки A_1 на прямые AB, AC, и плоскость ABC. Что тогда можно заметить? Какие принципиально разные случаи есть падения высоты на плоскость ABC?

Подсказка 2

Есть два случая - падение во внутрь призмы и во вне. Однако, при всем этом, у нас расстояния от точки A_1’(основание высоты) до прямых AB и AC равны, в силу равенства прямоугольных треугольников. Как тогда можно равносильно переформулировать случаи, когда высота падает во внутрь, а когда наружу? Как связать это с равноудаленностью от сторон?

Подсказка 3

Все верно, либо точка основания высоты лежит на внешней биссектрисе, либо на внутренней(угла BAC). Давайте посмотрим на второй случай. Мы видим, что прямые AA’ и A_1A’ перпендикулярны BC. Что тогда это значит? Чем это хорошо в нашей картинке?

Подсказка 4

Тем, что тогда BB_1 перпендикулярен BC, а значит BB_1C_1C - прямоугольник. Но тогда, если сторона треугольника в основании равна а, выходит, что a * AA_1 = 2, a * A_1K = 3. Тогда, пришли к противоречию, так как A_1K > AA_1. Значит, остался второй случай. Если прямая внутренней биссектрисы, была перпендикулярна прямой BC, то внешняя биссектриса будет…

Подсказка 5

Параллельна! А тогда, высота в параллелограмме CC_1B_1B - высота призмы. Значит, остается найти C_1H. Ну, а это уже чисто дело техники(и нескольких теорем Пифагора).

Показать ответ и решение

Если бы призма была прямая, то площади боковых граней были бы равны. Значит, призма наклонная.

Обозначим призму $ABCA1B1C1,$ площади из условия $SAA1B1B = SAA1C1C = 3.$

Пусть $A1K, A1M$ — высоты параллелограммов $AA1B1B$ и $AA1C1C.$ Тогда $A1K = A1M,$ т.к. площади равны, а также равны их основания, так как равносторонний треугольник.

Пусть $′ A$ — проекция $A1$ на плоскость $ABC.$ Тогда $′ ′ A K = AM,$ следовательно, точка равноудалена от прямых $AB$ и $AC.$

(a) Рассмотрим случай, когда $′ A$ принадлежит биссектрисе $AL$ угла $∠ABC.$ $AL$ — высота, медиана и биссектриса в равностороннем треугольнике.

$PIC$

AL ⊥ BC } ′ A1A′ ⊥ BC =⇒ BC ⊥(AA1A ) =⇒ BC ⊥ AA1 =⇒ BC ⊥ BB1

Тогда получаем, что $BB1C1C$ — прямоугольник. Пусть сторона треугольника $ABC$ равна $a.$ Посчитаем площадь прямоугольника и параллелограмма.

S1 =a ⋅AA1, S2 = a⋅A1K

2 =a ⋅AA1, 3= a⋅A1K

Но $A1K < AA1,$ тогда

3= a⋅A1K < a⋅AA1 = 2

получаем противоречие.

(b) Рассмотрим случай, когда $A′$ принадлежит внешней биссектрисе $AL$ угла $∠ABC.$

$PIC$

AA′ ∥BC )|} A1A∥BB1 =⇒ (AA1A′) ∥(BB1C ) AA′ ∥BC |)

Но $(AA1A′)⊥(ABC ),$ следовательно, $(BB1C)⊥ (ABC ),$ откуда следует, что высота $CH1$ параллелограмма $CC1B1B$ совпадает с высотой призмы $(C1H = A1A′).$ В итоге

V = SABC ⋅CH1 = 4√3

Ответ:

$√43-$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#37324

Докажите, что биссектор (плоскость, проходящая через ребро двугранного угла и делящая его на два равных двугранных угла) двугранного угла при ребре тетраэдра делит противоположное ребро на части, пропорциональные площадям тех граней тетраэдра, которые лежат на гранях этого двугранного угла.

Подсказки к задаче

Подсказка 1

Не правда ли, задача напоминает аналогичную в планиметрии с биссектрисой, только теперь вместо биссектрисы плоскость. Там мы доказывали это, выражая отношение площадей двумя способами и приравнивая их. А через что можно выразить нужные отношения в стереометрии?

Подсказка 2

Верно, можно сделать то же самое через объёмы тетраэдров, на которые разбивает биссектор исходный тетраэдр. Тогда выразим отношение объёмов через нужные площади и отрезки. Сначала давайте сделаем это для площадей, вспомнив, что мы ещё не пользовались равенством углов.

Подсказка 3

Ага, это равенство отношений мы получили. Теперь осталось получить его для отрезков. Давайте попробуем просто опустить высоты на общую грань тетраэдров. Чем тогда можно воспользоваться из планиметрии, чтобы связать высоты и отрезки грани?

Показать ответ и решение

$PIC$

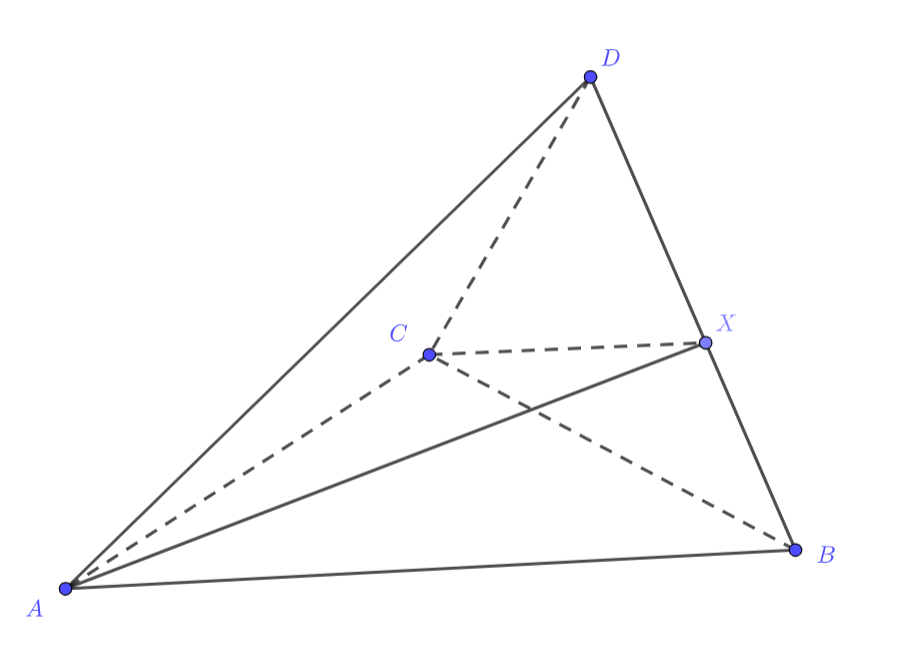
Пусть $XT$ — высота треугольника $ACX$ , а угол между плоскостями $ABC$ и $ACD$ равен $2α.$

С одной стороны (расстояние от $X$ до грани по следствию из теоремы о трёх перпендикулярах падает на перпендикуляр, восставленный из точки $T$ в плоскости соответствующей грани):

VACDX-= h(X,ACD-)⋅SACD-= XT-sinα-⋅SACD = SACD- VACBX h(X,ABC )⋅SABC XT sin α⋅SABC SABC

С другой стороны (отношение расстояний до общей грани переписывается через отношение наклонных из подобия прямоугольных треугольников):

VACDX- h(D,ACX-)⋅SACX- h(D,ACX-) XD- VACBX = h(B,ACX )⋅SACX = h(B,ACX ) = XB

Ответ:

что и требовалось доказать

Ошибка.
Попробуйте повторить позже

Задача 3#63817

В основании четырёхугольной пирамиды $ABCDS$ лежит параллелограмм $ABCD$ . На ребре $SB$ отмечена точка $E$ , так что $SE :EB = 2:1$ . На ребре $SD$ отмечена точка $F$ , так что $SF :FD = 1:2$ . Найдите отношение, в котором плоскость $AEF$ делит объём пирамиды.

Источники: ДВИ - 2020, вариант 205, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Попробуем как-то воспользоваться данными в условии отношениями…быть может, сделаем такое дополнительное построение, чтобы указанные в условии отрезки были в подобных треугольниках?

Подсказка 2

Проведите через точки B, C, D прямые, параллельные AS, и отметьте их точки пересечения B’, C’, D’ соответственно с плоскостью AEF. Что можно сказать о B’B, C’C, D’D?

Подсказка 3

B’B = 1/2 AC, D’D = 2AS, C’C = 5/2AS. Давайте теперь подумаем, как нам было бы удобнее считать объём? Быть может, разбить нашу пирамиду на несколько частей поменьше?

Подсказка 4

Выразите объем пирамиды через объемы ABDS и BCDS

Показать ответ и решение

Проведём через точки $B,C,D$ соответственно прямые $l ,l ,l B C D$ , параллельные $AS$ . Обозначим через $B′,C′,D′$ соответственно точки пересечения плоскости $AEF$ с прямыми $lB,lC$ , $lD$ .

$PIC$

Тогда $BB ′ = 12AS,DD ′ =2AS$ , откуда $CC′ = 52AS$ . Пусть $G−$ точка пересечения плоскости $AEF$ с $CS$ . Тогда $SG :GC = 2:5$ . Далее,

VAEGFS = VAEFS +VEGFS = 2⋅ 1 ⋅VABDS + 2⋅ 1⋅ 2⋅VBCDS = 3 3 3 3 7

= 2⋅ 1+ 2⋅ 1 ⋅ 2⋅ 1V = 1V . 3 3 3 3 7 2 ABCDS 7 ABCDS

Стало быть, искомое отношение равно $1:6.$

Ответ:

$1 :6$

Ошибка.
Попробуйте повторить позже

Задача 4#43960

Основание треугольной пирамиды $ABCD$ — правильный треугольник $ABC.$ Объём пирамиды равен $2√5 3$ , а её высота, проведённая из вершины $D$ , равна $3.$ Точка $M$ — середина ребра $CD.$ Известно, что радиусы сфер, вписанных в пирамиды $ABCM$ и $ABDM$ , равны между собой.

(a) Найдите возможные значения угла между гранями пирамиды при ребре $AB.$

(b) Найдите все возможные значения длины ребра $CD$ , если дополнительно известно, что грани $BCD$ и $ABC$ взаимно перпендикулярны.

Источники: Физтех-2017, 11.7 (см. olymp.mipt.ru)

Подсказки к задаче

Пункт а), подсказка 1

Как можно применить данные о равенстве радиусов сфер, вписанных в пирамиды? В условиях, когда известен объём, хочется подумать о формуле, связывающей радиус с объёмом и площадью поверхности. (Если такая вам неизвестна, попробуйте её вывести по аналогии с планиметрическим S = p*r)

Пункт а), подсказка 2

Итак, что мы видим: одна грань у этих пирамид общая, две другие попарно равновелики, так как М является серединой CD. Что в этом случае можно сказать об оставшейся паре граней?

Пункт а), подсказка 3

У нас появились равные по площади грани! Известный объём пирамиды и высота к одной из них помогут нам отыскать площади этих граней. Нетрудные вычисления откроют нам ещё и длину высоты грани ADB.

Пункт а), подсказка 4

Проведите высоту к основанию АВС Данной пирамиды и её апофему в грани ADB. Какая теорема поможет нам достроить имеющуюся конструкцию до линейного угла двугранного угла? Мы знаем достаточно, чтобы найти триг. функцию от искомого угла! Не забывайте только — нам никто не говорил что искомый уголочек будет острым ;)

Пункт б), подсказка 1

Какой вывод о расположении высоты пирамиды мы можем сделать из перпендикулярности двух её граней?

Пункт б), подсказка 3

Осталось снова применить теорему Пифагора и искомое ребро у нас в кармане :) Только будьте внимательны: совсем не обязательно высота нашей пирамиды будет падать именно на ребро, а не на его продолжение!

Показать ответ и решение

Воспользуемся формулой радиуса вписанной сферы $r= 3V S$ , где $V$ — объём, а $S$ — площадь поверхности пирамиды. Объёмы пирамид $ABCN$ и $ABDM$ равны (грань $ABM$ общая, а вершины $C$ и $D$ равноудалены от плоскости $ABM$ ); кроме того $SADM = SACM$ и $SBDM =SBCM$ (медиана делит площадь треугольника пополам). Значит, равенство сфер, вписанных в пирамиды $ABCN$ и $ABDM$ , эквивалентно условию $SABD = SABC$ или равенству высот, проведённых к стороне $AB$ в треугольниках $ABD$ и $ABC$ .

$PIC$

Пусть $DH$ высота пирамиды, а $DK$ высота в треугольнике $ABC$ . Объём пирамиды равен $√253-$ , а её высота из вершины $D$ равна 3, то есть $DH$ . Значит, площадь основания пирамиды равна $2√53$ . Тогда сторона основания $AB = 1√03$ , а высота треугольника $ABC$ равна 5. Значит, $DK$ также равно 5. Из прямоугольного треугольника $DHK$ находим $KH = √KH2-−-DH2-= 4$ , т.е. точка $H$ находится на расстоянии 4 от прямой $AB$ ( $H$ лежит на одной из двух прямых, параллельных $AB$ , на расстоянии 4 от неё). Тем самым, угол между гранями при ребре $AB$ равен $arccos± 4 5$ .

$PIC$

Из условия, что грани $BCD$ и $ABC$ взаимно перпендикулярны, следует, что $H$ лежит на $BC$ . Так как $KH = 4$ , то $8 HB = √3$ . Значит $CH = CB ±HB = 2√3$ или $1√83$ . Тогда $---------- ∘ -- CD = √CH2 +HD2 = 331$ или $-- 3√ 13$ .

Ответ:

$(a) arccos±4 5$

$√3√1 (b) 3$ или $√-- 3 13$

Ошибка.
Попробуйте повторить позже

Задача 5#51629

На ребре $CC 1$ правильной треугольной призмы $ABCA B C 1 1 1$ выбрана точка $M$ так, что центр сферы, описанной около пирамиды $MAA1B1B,$ лежит в грани $AA1B1B.$ Известно, что радиус сферы, описанной около пирамиды $MABC,$ равен $5,$ а ребро основания призмы равно $√- 4 3$ . Найдите:

(a) отношение объёма пирамиды $MAA1B1B$ к объёму призмы

(b) длину отрезка $MC$

Источники: Физтех-2012, 11.6 (см. olymp.mipt.ru)

Показать ответ и решение

$PIC$

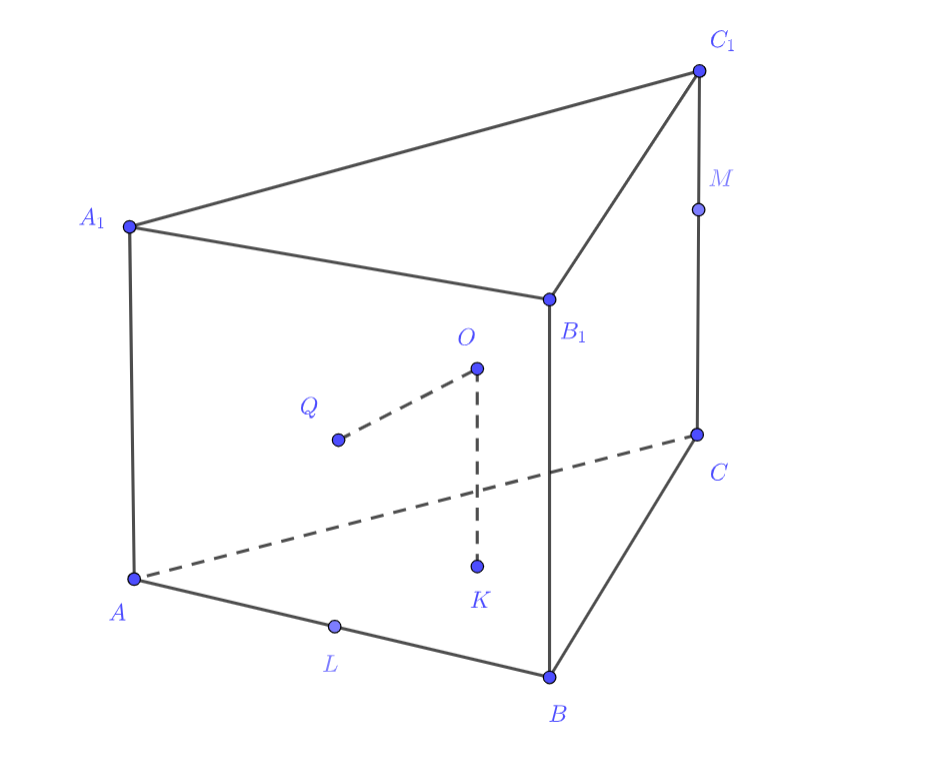
Введём обозначения: $K$ — центр грани $ABC; L−$ середина ребра $AB; Q$ — центр сферы, описанной около пирамиды $MAA1B1B$ (т.е. $Q$ — центр грани $AA1B1B$ ); $O$ — центр сферы, описанной около пирамиды $MABC$ .

(a) $-VMABC---= 1 ⋅ MC-;-VMA1B1C1-= 1⋅ MC1-⇒ VMABC+VMA1B1C1 = 1⋅ MC+MC1 = 1, VABCA1B1C1 3 CC1 VABCA1B1C1 3 CC1 VABCA1B1C1 3 CC1 3$ 3начит, объём пирамиды $MAA1B1B$ составляет две трети объёма призмы.

(b) Сторона равностороннего треугольника $ABC$ равна $√- 4 3$ , следовательно, $√- 1√- CK =4 3 ⋅ 3 = 4$ , как радиус описанной окружности.

Рассмотрим прямоугольную трапецию $CKOM$ . В ней известны стороны $CK =4,OM = 5$ и диагональ $OC = 5.$ По теореме Пифагора из треугольника $OCK$ находим, что $OK = 3.$ Опустим из точки $O$ перпендикуляр $OH$ на отрезок $MC$ . Тогда $MC =2 ⋅CH =2⋅KO = 6.$

∘ ------ ∘----------- h h2 ∘ --2-----------2 ( h )2 QL = 2,QB = 4 + 12,QM = CL + (QL− MC ) = 2 − 6 + 36

Отрезки $QB$ и $QM$ равны как радиусы сферы. Решая получающееся уравнение, находим, что $h = 10.$ Тогда площадь поверхности призмы $√- √- √- √ - S = 2⋅43⋅(4 3)2 +3⋅10⋅4 3= 144 3.$

Ответ:

(a) $2:3$

(b) $6$

Ошибка.
Попробуйте повторить позже

Задача 6#90596

На ребре $AS$ треугольной пирамиды $SABC$ отмечены такие точки $M$ и $N$ , что $AM = MN =NS$ . Найдите площадь треугольника $NBC$ , если площади треугольников $ABC,MBC$ и $SBC$ равны 2, 1 и $√- 2 7$ соответственно.

Показать ответ и решение

Пусть $S = 1,S = 2,S ,S = √37 1 2 3 4$ — площади треугольников $ABC, MBC, NBC,SBC$ соответственно, а $h ,h,h ,h 1 2 3 4$ — их высоты, опущенные на общее основание $BC :$

$PIC$

Обозначим через $A′$ , $B′,C′,S′,M ′,N′$ ортогональные проекции точек $A,B,C$ , $S,M,N$ соответственно на некоторую плоскость, перпендикулярную ребру $BC :$